基于模拟退火并行遗传算法的Otsu双阈值医学图像分割

许良凤， 林 辉， 胡 敏， 吴东升， 徐元英， 景 佳

（1. 合肥工业大学计算机与信息学院，安徽 合肥 230009；2. 合肥工业大学应用物理系，安徽 合肥 230009；3. 合肥工业大学科研处，安徽 合肥 230009；4. 中国科学院等离子体物理研究所，安徽 合肥 230031）

基于模拟退火并行遗传算法的Otsu双阈值医学图像分割

许良凤1， 林 辉2， 胡 敏1， 吴东升3， 徐元英2， 景 佳4

（1. 合肥工业大学计算机与信息学院，安徽 合肥 230009；2. 合肥工业大学应用物理系，安徽 合肥 230009；3. 合肥工业大学科研处，安徽 合肥 230009；4. 中国科学院等离子体物理研究所，安徽 合肥 230031）

模拟退火和并行遗传算法是两种较好的改进进化算法性能的方法。将这两种思想有机地结合起来，利用遗传算法能全局寻优的优势和模拟退火算法的爬山性能，提出了一种基于模拟退火并行遗传算法的Otsu双阈值医学图像分割算法。在该算法中，进化在多个不同的子群中并行进行，利用模拟退火算法的爬山性能，避免单种群进化过程中出现的过早收敛现象，提高整个算法的收敛速度。实验证明，这种新的图像分割算法与并行遗传算法相比，不仅能够对图像进行准确的分割，而且具有更强的精确性和稳定性。其收敛速度明显比并行遗传算法的Otsu双阈值医学图像分割快。

医学图像分割；Otsu；并行遗传算法；模拟退火

医学图像是临床医生和专家进行疾病诊断的重要依据，而医学图像分割技术就是将图像中感兴趣的观察目标提取出来，以有利于医学研究和临床诊断。由于医学图像的解剖组织结构和形状十分复杂，加上本身具有的模糊和不均匀等特点，另外还受到图像噪声，成像质量等诸多因素的影响，传统的图像分割方法显得很困难，因此在这个领域已出现了许多不同的图像分割方法[1]。

常用的图像分割方法包括灰度阈值法，边缘检测法等[2]。这些方法要求目标和背景之间有明显的灰度变化。但是在实际情况中，由于光照、对焦等影响，这种明显的灰度变化很难出现。因此人们提出了许多新的图像分割的方法，比较有代表性的如Kapur 等人提出的最佳熵阈值法[3],以及1979年由N Otsu 提出的最大类间方差方法（Otsu法）[4]等。最大类间方差选择阈值的目的在于用几个阈值将图像的灰度直方图分成独立的类，使得各类间的方差最大。确定阈值是阈值化分割的关键，最佳阈值的确定是目前有待于解决的问题。根据阈值的个数，图像阈值分割可分为单阈值分割和多阈值分割。多阈值分割问题可转化为一系列单阈值分割问题来解决，但这需要在全灰度范围内搜索一个最佳门限组合，耗时较多，难于实际应用。为简化计算，可利用遗传、免疫等进化算法来搜索最佳阈值[5-6]。由于遗传算法容易导致过早收敛，使得算法的精确性、稳定性受到限制，且收敛速度也受到限制。

为了进一步改善这些弱点，本文在“基于并行遗传算法的Otsu双阈值医学图像分割”[7]一文的基础上将模拟退火和并行遗传算法有机地结合起来，利用遗传算法能全局寻优的优势和模拟退火算法的爬山性能设计了基于模拟退火并行遗传算法的Otsu双阈值医学图像分割，在该算法中，一方面利用了并行遗传算法将并行计算机的高速并行性和遗传算法天然并行性相结合，极大地提升了遗传算法的求解速度和质量；另一方面通过Boltzmann机制来接收子代，这样做有利于优良个体的保留。随着进化过程的进行，温度逐渐下降，接收劣质解的概率逐渐减小，即利用模拟退火算法的爬山性能提高整个算法的收敛速度。仿真结果表明，该算法能够准确、迅速地找到图像分割的最佳阈值，并对图像进行双阈值分割，具有较好的效果、较强的稳定性和精确性和较快的收敛速度。

1 基于最大类间方差阈值的图像分割

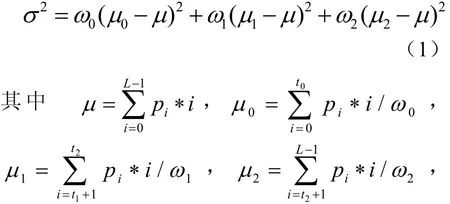
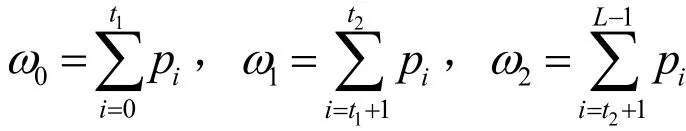
这样，利用最大类间方差法,图像的双阈值分割的阈值求解问题就可归纳为最佳阈值,的优化问题。

2 基于模拟退火并行遗传算法的Otsu双阈值医学图像分割

2.1 并行遗传算法

并行遗传算法主从处理器的结构图如文献[7]所示。首先主处理器将种群划分成若干个子种群给从处理器，然后各个子种群在不同的从处理器上相互独立的并发执行进化操作主循环，每运行完确定的代数以后，每个从处理器运行的遗传算法的主循环将接收上游相邻主循环的最佳染色体，并向下游相邻主循环传递自身的最佳染色体；如此运行下去直到终止条件满足为止。当算法结束时，每个从处理器就有一个最佳染色体，从处理器将各自的最佳染色体传给主处理器，主处理器取其中最佳染色体作为最后的结果。

2.2 模拟退火算法

模拟退火算法起源于统计物理学中对固体退火过程的模拟[8]。它采用Boltzmann接受准则接收新解, 用一个称为冷却系数的参数控制算法进程, 使算法在多项式时间里给出一个近似最优解。求解过程如下：

（1） 初始化退火温度Tk（令k=0），产生随机初始解X0；

（2） 在温度Tk下重复执行如下操作，直至达到温度Tk的平衡状态：

1） 在解x的领域中产生新的可行解x′；

2） 计算新解的评价函数 f (x′)和旧解的评价函数 f (x)的差值Δ f；

3） 依照概率min{1, exp (-Δf /Tk) }＞random[0, 1 ]接收新解，其中random [0, 1 ]是[0, 1 ]区间内的随机数。

（3） 令 Tk+1＝αTk，k←k+1，其中 α∈(0, 1)。若满足收敛判据，则退火过程结束；否则，转(2)。

2.3 基于模拟退火并行遗传算法的Otsu双阈值医学图像分割

由式(1)可知，图像双阈值分割的阈值求解问题是一个优化问题，结合模拟退火及并行遗传算法的特点，提出一种基于模拟退火并行遗传算法的 Otsu双阈值医学图像分割。每个处理器运行模拟退火遗传算法的主循环详细流程图如图1所示。

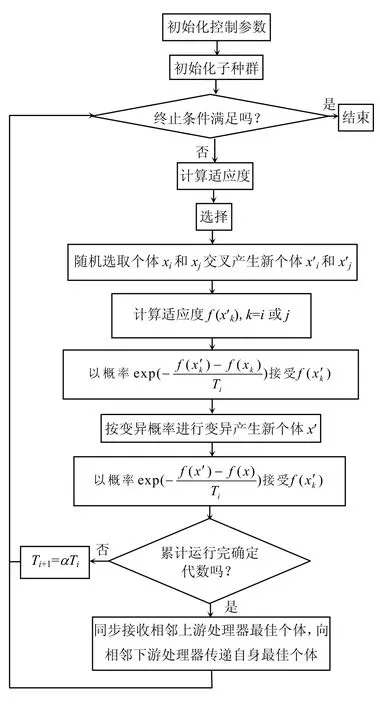
图1 每个从处理器模拟退火遗传算法的主循环流程图

（1） 种群初始化

在搜索空间随机产生N个个体作为初始种群，并计算每个个体的适应度。

（2） 编 码

由于图像灰度值在0～255之间，故将各个染色体编码为16位二进制码，前8位代表一个分割阈值，后8位代表另一个分割阈值。

（3） 适应度函数

采用式(1)作为适应度函数。

（4） 选 择

采用进行赌轮法（蒙特卡罗法）。

（5） 交 叉

采用双点交叉，两个交叉点分别在前8位和后8位随机产生，对随机匹配交叉的个体的部分串（在交叉点后）进行互换。

（6） 变 异

按变异概率随机地改变前8位和后8位中某一个串位的值(即取反)。

3 结果与分析

为验证本文算法的有效性，作者将本文算法与并行遗传算法分别对图像进行分割实验并作对比。实验中模拟退火并行遗传算法的参数如下：从处理器的个数为2，每个从处理器处理种群的个体总数为10，变异概率为Pm=0.1，交叉概率为Pc=0.6，温度冷却系数α = 0.9，退火初始温度T =999，迭代代数为150。对两种算法分别进行了100次独立实验。

3.1 分割结果比较

图2(a)是脑部MR原始图像(512×512)，根据穷尽搜索的结果，真实阈值为（51, 150）。

两种算法100次计算所得平均阈值并取整都与真实阈值相同，即使用双阈值t1=51，t2=150（与真实值相同）的分割结果如图2(b)所示。

图2 分割结果

3.2 算法稳定性和精确性比较

表1列出了各个算法所得结果的平均值、绝对误差、相对误差和方差，对比了基于并行遗传算法的Otsu双阈值（算法1）与基于模拟退火并行遗传算法的Otsu双阈值医学图像分割（算法2）两种算法的性能。平均值、绝对误差和相对误差代表了算法的精确性，而方差则说明了算法的稳定性。可以看出，不论是在精确性，还是在稳定性上，本文算法相对算法1都更接近真实值，且各次计算结果的波动更小，更为稳定。

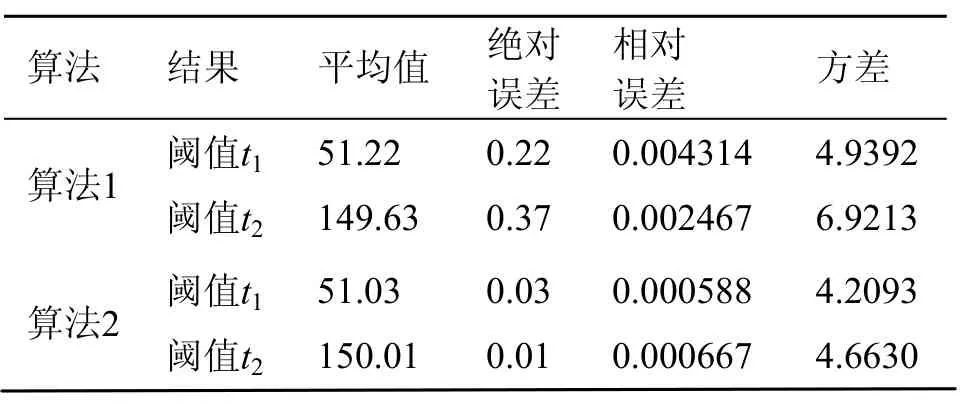
表1 算法性能对比

3.3 算法收敛速度比较

图3是100次实验的统计平均结果曲线，图中每一进化代的适应度值均为100次平均的结果。

图3 平均进化曲线图

由图3可以看到基于模拟退火并行遗传算法的Otsu双阈值的收敛速度比基于并行遗传算法的Otsu双阈值医学图像分割的收敛速度要快。基于模拟退火并行遗传算法的Otsu双阈值医学图像分割经过约4代的种群迭代后收敛，而基于并行遗传算法的Otsu双阈值医学图像分割则要经过约15代的种群迭代后收敛。

4 结 论

本文将模拟退火和并行遗传算法两种思想有机的结合起来，建立了一种基于模拟退火并行遗传算法的 Otsu双阈值医学图像分割，对比实验说明，本文提出的模拟退火并行遗传算法的Otsu双阈值成功地应用于医学图像分割，不仅保持了模拟退火并行遗传算法比并行遗传算法收敛速度快的特点，在不增大运算复杂度的情况下，在优化阈值的搜索性能方面表现出了一定的优势，提高了搜索的准确性与稳定性。

[1]林 瑶, 田 捷. 医学图像分割方法综述[J]. 模式识别与人工智能, 2002, 15(2)：192-204.

[2]章毓晋. 图像工程(中册)(第2版)[M]. 北京：清华大学出版社, 2005. 73-201.

[3]Kapur J N, Sahoo P K, et al. A new method of gray-level picture thresholding using the entropy of the histogram [J]. Computer Vision, Graphics, and Image Processing, 1985, 29(3)：273-285.

[4]Otsu N. A threshold selection method from gray-level histograms [J]. IEEE Transactions on Systems, Man and Cybernetic, 1979, 9(1)：62-66.

[5]Ujjwal Maulik. Medical image segmentation using genetic algorithms [J]. IEEE Transactions on Information Technology in Biomedicine, 2009, 13(2)：166-173.

[6]李 映, 赵荣椿, 张艳宁, 等. 基于自适应免疫遗传算法的图像分割[J]. 模式识别与人工智能, 2005,18(2)：193-197.

[7]许良凤, 林 辉, 罗 珣, 等. 基于并行遗传算法的Otsu双阈值医学图像分割[J]. 工程图学学报, 2011,32(2)：88-92.

[8]康立山. 非数值并行算法(第 1册)——模拟退火算法[M]. 北京：科学出版社, 1997. 22-55.

An Otsu Dual-threshold Value Method Based on Simulated Annealing Parallel Genetic Algorithm for Medical Image Segmentation

XU Liang-feng1, LIN Hui2, HU Min1, WU Dong-sheng3, XU Yuan-ying2, JING Jia4
( 1. School of Computer and Information, Hefei University of Technology, Hefei Anhui 230009, China;2. Application Physics Department, Hefei University of Technology, Hefei Anhui 230009, China;3. Research and Administration Department, Hefei University of Technology, Hefei Anhui 230009, China;4. Institute of Plasma Physics, Chinese Academy of Sciences, Hefei Anhui 230031, China )

Simulated annealing and parallel genetic algorithm are two helpful methods which can improve the performance of evolutionary algorithm. The paper applies the global optimum performance of evolutionary programming and the hill climbing performance of simulated annealing, and proposes an Otsu dual-threshold value method based on simulated annealing parallel genetic algorithm for medical image segmentation. In the algorithm, evolutions of subgroups are performed among subgroups in parallel, and the hill climbing performance of simulated annealing is utilized, so this algorithm avoids premature convergence of alone group evolutionary process and improves its convergence efficiency. Experiments show that this new algorithm can achieve exact image segmentation and is of better accuracy and stability than parallel genetic algorithm, and its convergence speed is faster than the Otsu dual-threshold value method based on parallel genetic algorithm.

medical image segmentation; Otsu; parallel genetic algorithm; simulated annealing

TP 391.41

A

1003-0158(2011)05-0025-05

2010-03-09

国家自然科学青年基金资助项目（10805012）

许良凤（1970-），女，安徽肥东人，副教授，硕士，主要研究方向为多媒体通信，图像处理。