马尔可夫链在奖惩系统中的应用

王丙参，魏艳华，戴宁(.天水师范学院数学与统计学院，甘肃天水7400;.郑州大学数学系，河南郑州45000)

马尔可夫链在奖惩系统中的应用

王丙参1，魏艳华1，戴宁2
(1.天水师范学院数学与统计学院，甘肃天水741001;2.郑州大学数学系，河南郑州450002)

文中论述了Markov链的基本原理，根据实例在汽车保险中建立了马尔可夫奖惩系统，并分析了经济含义.关键词:Markov链;转移概率;奖惩系统

随着我国保险市场的全面开放，保险公司之间的竞争也越来越激烈，“奖惩系统”的作用越来越受到保险公司的重视.“无赔款优待系统”是“奖惩系统”的一种，在续保时，对有索赔记录的投保人在保费上给予一定的惩罚;而对无索赔记录的投保人给予一定的奖励.目的是使保险公司能收取更真实反映保险标的风险的保险单，鼓励那些出险较少地被保险人继续留在同一保险公司续保.对保险公司而言，对投保人的逆选择问题可以起到预测或抑制作用，通过客观的评价每个人的风险，并在此基础上使每个保单持有人缴纳的保费与其风险大小成比例，从而激励投保人提高安全意识，即可以规避风险，又可以留住优质保单，提高经营效益;对被保险人而言，又可以降低保险费，提高投保积极性.“无赔款优待系统”在汽车保险中的作用越来越受到各国政府的重视，各国根据自己的实际国情在发展的过程中适时对已有无赔款优待系统制度进行不断的完善［1－3］.奖惩系统是马尔可夫过程的特殊情形，马尔可夫分析可以帮助我们判断在确定代表驾驶员实际风险的调整保费时奖惩系统的效果如何，因此，本文利用马尔可夫链建立了奖惩系统模型，从而刻画了顾客实际风险调整时保费如何变化并分析了经济含义.

1 基本概念

定义在(Ω，F，P)上的马尔可夫链{X(n)，n∈T}，其中指标集T={0，1，2，…}，状态空间I={i0，i1，…}，称Pij(n)=P{Xn+1=j|Xn=i}为在时刻n的一步转移概率，简称转移概率.如果上式的条件概率与n无关，则称为齐次马尔可夫链.称条件概率=P{X=j|X=i}，i，j∈I，m0，n1为m+nmn步转移概率，p(n)=()为n步转移矩阵，其中0，i，j∈I，=1，i∈I，.显然具有下列性质:

2 奖惩系统模型

汽车保险是非寿险的一个重要分支，在许多国家汽车险甚至在总保费收入中占的比例最大.保险的本质在于“幸运的”保单持有人为“不幸运的”保单持有人买单.但在私营保险中，利益共同体不应该导致“好的”被保险人固有地要为另一个“差的”被保险人买单这样的一个局面.若保险人试图将这种补贴利益共同体强加于客户，他将会看到“好的”被保险人纷纷离他而去，而留下的只是“差的”被保险人，也就是劣币驱赶良币.经验费率系统中的奖励被视为对细心的驾驶员的一种奖赏，而对于事故频发的驾驶员来说，增加的保费被视为对他追加的罪有应得的罚款.在汽车保险中使用奖惩系统的主要目的是:(1)公平保费负担，使被保险人缴纳的保险费反映真实的风险水平;(2)降低保险公司受理小额理赔的费用，因为被保险人为了获得保费奖励，会自付小额理赔;(3)鼓励被保险人在驾车时更加小心谨慎，主动控制风险.不过，奖惩系统在实际中也受到了一些批评，如:(1)破坏了被保险人的经济稳定性.被保险人购买保险就是为了通过缴纳固定的保险费将不确定的风险转嫁给保险人，但在奖惩系统下，被保险人还得承担续期保费的变异性;(2)被保险人的互助合作关系削弱了;(3)违背了大数定律，即有组织的抛弃了保险原则.但尽管如此，奖惩系统在实践中仍然得到了广泛的应用［5］.

驾驶员本身的状况称为自身的状态，我们假定有n个状态的.设在一个特定的奖惩系统中有一个驾驶员，如果他在第i－1，i年中有理赔记录，那么他在i+1年需要缴纳一个较高的保费ci+1;如果他在第i－1年中有理赔记录而在第i年无理赔记录或者第i年中有理赔记录而在第i－1年无理赔记录，那么他在i+1年需要缴纳一个保费ci;否则他只需要缴纳保费ci－1，ci－1＜c1＜ci+1.设一个驾驶员在一个保单年度里发生一个或多个理赔的概率为p，q=1－p，则我们得到下面具有转移概率为pij的转移矩阵

其中a=q2，b=1－a－c，c=.记，i∈I表示由状态i出发，经n步首达i的概率，μi=表示由i出发再返回i的平均返回时间.

定理2［4］不可约非周期马尔可夫链是正常返的充要条件是存在平稳分布，且此平稳分布就是极限分布{i/μj，j∈I}.

由于有限状态的不可约非周期马尔可夫链只有正常返态，故由定理2必存在平稳分布，而奖惩系统中的马尔可夫链是有限状态的非周期不可约马尔可夫链，故奖惩系统中的马尔可夫链必存在平稳分布.

如果驾驶员在初始时刻处于状态i=1，…，n的概率为PT(0)=(p1，p2，….pn)，则有m个周期之后处于状态i=1，…，n的概率为PT(m)=PT(0)p(m)= PT(m－1)P.由于存在平稳分布，不妨假设为π= {π1，…，πn}，则π=πP，我们可以通过软件求出数值解.显然平稳分布是P的特征根1的左特征向量.由定理2可得μ=(，…)，即司机从状态i，i= 1，2，…，n返回原来的状态平均所需要的时间分别是:μ=…)，年.如果假定个体保单索赔频n率服从P(λ)，其稳态概率分布就是πi(λ)，则其平均奖惩系数就是AP(λ)=π(λ)·c=πi(λ)ci.这种方法的重要意义在于可以发现交高额保费的司机，如果按照目前的状态和趋势发展，不对其采取有效的治理措施，保费回到低状态是很难的，因此必须加以干预，通过各种有效的措施来改善保费水平，如开车更加小心，雪天防滑等等.

设齐次马尔可夫过程{X(t)，t0}的状态空间I={0，1，…}，转移概率为pij(t)，如果

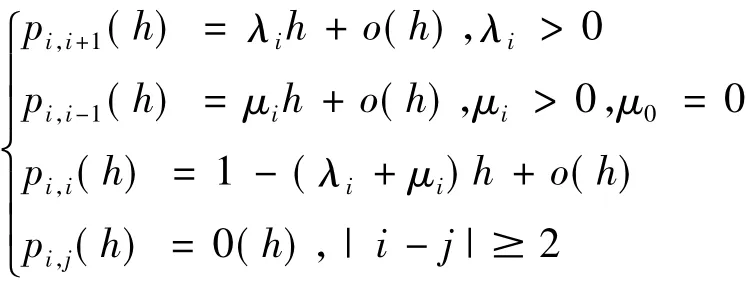
则称{X(t)，t0}为生灭过程，λi，μi分别称为出生率和死亡率.由定理1得

注意:当市场条件改变的时候，我们用此法得到的结果与现实差距太大，如果贸然使用，会出现错误，因此此时要特别分析［6］.

奖惩系统的最终目的是使得每个人缴纳的保费尽可能地接近于其年理赔额的平均值［7－8］.为了研究一个奖惩系统是否能有效地实现这个目的，则必须来看看保费是如何依赖于理赔频率λ的.稳定状态保费定义为b(λ)=π*(c1，…，cn)T，这就是在初始状态影响已经消失后要缴纳的平均保费，原则上这个保费应该与λ成比例，这是因为理赔频率数强度为λ的驾驶员的平均年理赔总额等于单个平均理赔额的λ倍，并且已经假定单个理赔额与理赔频数独立.称e(λ)==为Loimaranta功效，由于弹性系数=，所以e(λ)表示稳态保费b(λ)关于λ的弹性.计算弹性有一种近似方法，首先给出λ的一个值，计算对应的b(λ)的值，然后增加一个很小的量△λ，得到λ+△λ，再计算b(λ+△λ)，则得到索赔频率为λ的弹性近似值η(λ)=我们很容易利用软件求得不同的λ取值所对应的弹性系数.对于充分小的h，由泰勒展开可得b(λ(1+h))≈b(λ)+λh=(1+e(λ)h)，因此在理想的情况是功效应当满足e(λ)≈1，功效小于1意味着差驾驶员占便宜.由于稳态保费并不依赖于初始状态，所以其Loimaranta功效不依赖于初始状态，尽管两者均依赖于理赔频数λ.在各种系统中保费的百分比均为正的有限数，即b(0)＞0，b(∞)＜∞，但在很多实际的奖惩系统中有b(∞)＜∞，所以

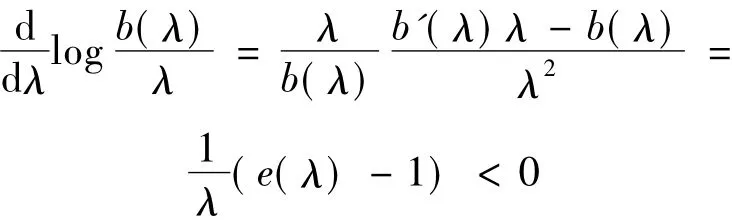
［1］马学思，刘次华.多级无赔款优待系统的研究［J］统计与决策，2008，22:49－51.

［2］张玲，陈秀丽.基于索赔额与应负责任的奖惩系统［J］数学理论与应用，2008，28(3):26－29.

［3］刘源，徐昕.保险精算中的多零索赔现象探析［J］统计与决策，2008，21:21－23.

［4］刘嘉锟，王公恕.应用随机过程［M］.北京:科学出版社，2004.

［5］孟生旺，刘乐平.非寿险精算学［M］.北京:中国人民大学出版社，2007.

［6］王丙参，魏艳华，田玉柱.马尔可夫链在市场占有率的应用［J］.通化师范学院学报，2009，30(2):7－9.

［7］R.卡尔斯等著，唐启鹤等译.现代精算风险理论［M］.北京:科学出版社，2005.

［8］张博著.精算学［M］.北京大学出版社，2005.

(责任编辑:王宏志)

F224.7

A

1008－7974(2011)04－0009－03

甘肃省自然科学研究基金计划(096RJZE106);天水师范学院科研基金(TSA0931).

2010－12－30

王丙参(1983－)，河南南阳人，硕士，天水师范学院数学与统计学院讲师.