声相关计程仪基阵设计方法

薛敬宏,金 铭,乔晓林

(哈尔滨工业大学(威海)信息工程研究所,山东 威海 264209)

声相关计程仪基阵设计方法

薛敬宏,金 铭,乔晓林

(哈尔滨工业大学(威海)信息工程研究所,山东 威海 264209)

针对声相关计程仪的测速特点,研究了一维、二维基阵的设计方法。一维基阵采用基于约束最小冗余的设计方法,可以获得比均匀线阵大得多的阵列孔径,从而提高基阵的利用率,但约束最小冗余线阵(RMRLA)的设计方法计算量巨大,并不适合二维基阵的设计。在重新定义冗余因子,建立理想位置矢量图模型,提出位置矢量重合率等概念的基础上,实现了适用于声相关测速需求的二维基阵的快速设计。仿真结果证明了该设计方法的可行性。

约束最小冗余线阵;冗余因子;位置矢量重合率;声相关计程仪;基阵

Abstract:A designmethod of one dimension and two dimension arrays for an acoustic correlation log(ACL)is studied.Based on themethod of restrictedminimum-redundancy linear array(RMRLA),non-uniform linear array has significant performance in comparisonwith uniform linear array,such as extending aperture and full utilization of sensors.But the algorithm does not adapt to two-dimensional arrays design due to huge computation and the imperfection of the positional vector set.In thispaper,the redundancy factor is redefined,an ideal positional vector map is built,the conceptionof positional vector coverage rate isproposed and a fast two-dimensional arrays designmethod isobtained.Simulation shows the feasibility of thismethod.

Key words:RMRLA;redundancy factor;positional vector coverage rate;ACL;arrays

在海底深度超过1 000m的情况下,利用“波形不变性原理”工作的声相关计程仪(ACL)[1]无论是在导航定位、海底勘探、海洋资源开发以及军事等领域,都有广阔的应用前景。

ACL采用垂直向海底发射编码单脉冲,利用多个阵元构成一个接收基阵。任意两个接收阵元产生大小相等方向相反的位置矢量,所有位置矢量组成一个矢量集合。根据不同阵元接收海底混响回波信号的相关性,可以形成位置矢量集合与相关系数之间的映射关系,利用不同的曲面拟合方法形成不同的测速方法。测速精度除了与发射波形、信噪比等因素有关,还与接收阵元的个数及基阵的分布形式有关。

国内外学者对基于一维线阵的设计进行了深入研究,Arsac[2]给出了无冗余线阵的设计方法,并将其应用于射电天文学中;在此基础上,Alan TMoffet提出了约束最小冗余线阵(RMRLA)的概念[3],使得在相同阵元的情况下,可以获得比均匀线阵大得多的位置矢量数,从而提高空间采样率;SW Lang[4]基于阵元位置矢量分布趋于均匀的理念,提出了适应于最大似然(MLM)和最大熵(MEM)估计算法的线阵设计。事实上,当阵元位置矢量分布均匀时,文献[4]可以归结为类似无冗余线阵的设计方法。刘学斌[5]将文献[3]中的范例进行归纳总结,提出了一种快捷的线阵设计方法,设计的基阵在结构上类似于均匀线阵,并将设计结果与基于RMRLA的结果进行了比较;国内其他学者采用RMRLA实现了MUSIC算法[6]、ESPRIT算法[7]、TLS-ESPRIT快速算法[8]等,既提高了阵列孔径的利用率,又不降低谱估计性能。基于RMRLA的一维线阵的设计方法最终归结为计算量巨大的基阵结构搜索过程。文献[5]虽然减少了计算量,但是设计的阵形结构受到限制。

由于线阵只能测量一维船速,因此即便是线阵平行于船龙骨放置,由于海流、风以及转弯存在船的惯性等原因,都需要测量二维船速。Yingbo Hua[9]研究了利用均匀线阵构成的“L”阵,并通过计算克拉美-罗界证明“L”阵比传统的简单2-D基阵,如十字交叉阵、方阵、三角阵等的克拉美-罗界要小,说明其测速精度要高;Robinson[10]在专利中详细介绍了由五阵元构成的非均匀线阵的结构及产生的位置矢量,并利用该五阵元非均匀线阵形成的5×5二维基阵用于二维测速;英国研制的相关测速计程仪COVELIA[11]采用6×6的均匀线阵构成二维测速基阵,利用该种基阵结构尽管产生的位置矢量冗余比较大,但是由于位置矢量在四象限均匀分布,有利于迭代算法的实现。文章在该种基阵结构的前提下,给出了最大似然和最小二乘算法的具体实现过程,并通过误差分析比较了各种算法的优劣。

由于“L”阵等简单二维阵位置矢量存在的缺陷,而文献[10-11]中所用阵元数较多,造成基阵尺寸增大,产生的位置矢量存在较大冗余。为了提高阵列孔径的利用率,郭纪捷[12]将利用较少阵元数产生的稀疏基阵分为均匀阵、蜂窝阵和非均匀阵三种,例如RDI[13]和中科院声学所[14]采用由8个接收阵元构成的稀疏基阵实现二维测速,并将差分方程的一部分算法结合到布阵技术中。文献[13-14]所采用的基阵形式在文献[12]中被称为均匀阵。

虽然上述文献中给出了很多二维基阵的具体结构,但是很少有文献给出实用的适用于ACL二维测速的基阵设计方法,文献[3]提出的约束最小冗余算法也不能直接应用于二维基阵的设计。在充分研究文献中二维基阵结构的基础上,基于最小冗余的设计原则,通过设计基阵形成的矢量图与理想矢量图模型的比较,得到适用于ACL二维测速的基阵设计。

1 基阵设计原则

1.1 最小冗余

一维线阵的设计大多基于RMRLA的概念,RMRLA中“约束”的含义指的是阵列中所有阵元形成的位置矢量集合必须是完备的,即若将所有非负位置矢量(正负对称)作归一化得到的一个集合,那么这个集合的取值将遍历0到最大整数间所有的整数。因此文献[3]通过定义冗余因子来衡量线阵的利用率:

式中:N为接收阵元数;Nmax为最大位置矢量间距,如果阵元位置矢量集合是完备的,Nmax也等于阵元位置所产生的非负位置矢量数。Bracewell[15]已经证明,只有一维线阵产生的阵元位置矢量集合才有可能是完备的。二维基阵结构通常是稀疏的,阵元位置矢量集合不满足完备性条件,因而重新定义二维基阵的冗余因子:

式中:P(N,2)=N(N-1)为N中选2的排列计算,加1则表示包含0位置矢量,M为由N个阵元产生的互不相同的位置矢量个数。

1.2 矢量图模型

以船的龙骨方向定义为x轴方向,则船速方向主要在x(或y)轴及偏离x(或y)轴方向的较小的夹角内变化,相比较而言,45°夹角附近的位置矢量利用率是非常低的,因此像文献[11]所产生四象限位置矢量均匀分布的布阵并非一种理想的选择。根据上述分析,在无需考虑具体布阵结构的情况下,可以得到一种理想的阵元位置矢量的二维分布图(如图1所示)。

图1 理想位置矢量图模型Fig.1 The ideal positional vectormap

图1所形成的位置矢量图为n×n的菱形分布,其中“○”代表不同阵元产生的位置矢量。考虑到二维基阵产生的位置矢量是有冗余的,因此理想位置矢量图中矢量个数的选取应比由接收阵元个数N确定的最大位置矢量数略小即可,例如接收阵元个数为8时,产生的位置矢量个数为57(包括零矢量),理想矢量图模型可选用7×7的菱形分布。

图2 二维基阵设计流程Fig.2 Flow chartof two-dimension arrays design

为了描述不同阵元结构分布所形成的位置矢量图与理想模型的接近程度,定义位置矢量重合率ρ满足:

取值范围为0≤ρ≤1。

1.3 满足声相关测速

在位置矢量重合率ρ相等的前提下,选择合理的基阵阵元布局应与声相关测速的算法相结合。在利用最大似然谱估计进行迭代时,如果某个方向的位置矢量间隔为非均匀的,则会由于栅瓣位置距离主瓣太近而产生测速误差,甚至测速结果远离真实值的情况。因此一个优化的阵元位置矢量分布图首先应该满足菱形内部无缺失,当菱形外部的四个边上的位置矢量有缺失时,首先保证靠近x轴方向的位置矢量无缺失,即满足“先内后外”、“先x轴后y轴”的原则。上述原则的实现,可以通过不同的阵元位置矢量赋予不同的加权系数的方式实现,当基阵结构数较少时,也可直接通过人工的方式进行选择。

1.4 设计流程

根据上述设计原则,可以得到二维基阵的设计流程如图2所示。下面将以8个接收阵元为例说明二维接收基阵的设计过程。

2 仿真举例

假设所有接收阵元都是尺寸相同的且方向图为各向同性的,分布在均匀的网格中(文献[12]中的均匀阵设计),每个阵元的直径为6.7 cm,采用5×5的均匀网格如图3所示。

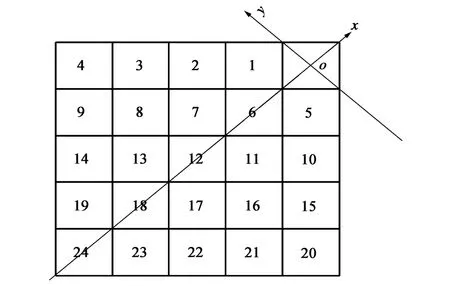
图3 阵元分布网格示意Fig.3 The gridsof the distribution of array elements

坐标系原点o为发射换能器位置,坐标系的选取保证接收阵元位置都在发射阵元的同侧,即接收阵元分布的位置共有24个,这样不同的基阵分布形式共有C(24,8)=735 471种,其中C(n,m)代表n中选m的组合关系。

首先选取冗余因子较小的基阵结构,即假设M取一较大数值,根据式(2)计算冗余因子作为基阵结构筛选的一次门限,根据筛选后的基阵个数确定是否需要增大或减小M的取值,选取M=50,即设定门限值Rthreshhold=1.14,选取冗余因子R≤Rthreshhold的布阵形式,结果满足需要的共有7 969种基阵结构。

然后选取7×7的菱形分布作为理想位置矢量图模型,在满足上述要求的基阵结构中,选取位置矢量重合率最高的阵元分布形式,仿真可得ρ=0.51～0.92,选取ρmax=0.92,由仿真结果可得,满足要求的阵元分布共有32种。在32种阵元分布结构中,满足1.3节原则的只有如下一种分布,见图4。

图4 8阵元分布和位置矢量Fig.4 An 8 elements transducer array and the positionalmap

从上面的例子可以看出,每一种设计原则(或称为约束条件)的采用,都会使搜索的范围降低两个数量级,因而计算量大大减少了,从最后得到的结果来看,图4所示的基阵结构实际上是文献[13-14]所采用基阵结构的旋转变形。

图5、图6所示为采用上述原则设计的6阵元和10阵元基阵结构及其位置矢量图。理想位置矢量图模型分别选用5×5和9×9的菱形分布。

图5 6阵元分布和位置矢量Fig.5 A 6 elements transducer array and the positionalmap

由仿真结果可得,图5和图6对应的冗余因子分别为1.00和1.28,位置矢量重合率分别为0.92和0.88。相比较8阵元基阵设计中的冗余因子和位置矢量重合率分别为1.12和0.92而言,6阵元基阵产生的位置矢量尽管没有冗余。但由于产生的位置矢量个数较少,在进行速度结算时,由于空间采样点数的减少会影响测速精度。当然从图5(a)阵元分布可以看出,与8阵元和10阵元基阵相比,在阵元直径相同的情况下,其基阵尺寸可以明显减小。而10阵元基阵尽管位置矢量个数有所增加,但冗余度增大而位置矢量重合率降低,因此在基阵尺寸一定的情况下,阵元的个数不宜太多。

3 结 语

二维基阵产生的位置矢量集合不满足完备性条件,因而无法采用像一维基阵一样的约束最小冗余的设计方法,而且该方法计算量巨大,通过重新定义冗余因子、构建理想位置矢量图模型,同时考虑ACL测速计算的需求,实现了简单而实用的二维基阵的设计。

[1] Steven EBradley.Correlation Sonar System[P].U.S.Patent No:5,315,562,1994.

[2] JArsac.Nouveau reseau pour l′observation adioastronomique de la brillance sur le soleil a 9350Mc/s[C] ∥Compt.Rend.Acad.Sci.1995,240:942-945.

[3] Alan TMoffet.Minimum-redundancy linear arrays[J].IEEE Transactionson Antennas and Propagation,1968(2):172-175.

[4] SW Lang,GL Duckworth,JHMcClellan.Array design forMEM and MLM array processing[C]∥Proc.ICASSP-81.1981:145-148.

[5] 刘学斌,季 飞,韦 岗.一种简单快捷的完全可扩展线阵设计[J].电视技术,2005,2:32-34.

[6] 金 梁,王雪明,姚敏立.基于最小冗余线阵的谱相关共轭循环MUSIC算法[J].信息工程学院学报,1999,18(3):4-7.

[7] 姚敏立,金 梁,殷勤业.一种基于最小冗余线阵的时空共轭循环谱相关ESPRIT算法[J].电子科学学刊,2000,22(1):35-41.

[8] 于 波,杨莘元.基于约束最小冗余线阵的TLS-ESPRIT快速算法[J].应用科技,2004,31(5):34-36.

[9] Yingbo Hua,Tapan K Sarkar,Donald DWeiner.An L-shaped array for estimating 2-D directionsof wave arrival[J].IEEE Transactionson Antennas and Propagation,1991,39(2):143-146.

[10] Robinson Henry.Transducer for Acoustic Correlation Velocity Log,WO 97/47990[P].1997.

[11] PBoltryk,M Hillt,A Keary,et al.Improvementof velocity estimate resolution for a correlation velocity log using surface fittingmethods[C]∥Oceans 2002.2002:1840-1848.

[12] 郭纪捷,荀俊姑,徐正高.声相关海流剖面(ACCP)测量的接收阵元分布形式对流速估计值的影响[C]∥水声换能器和基阵技术讨论会论文集.1999:39-41.

[13] G Griffiths,SEBradley,GWatson,et al.Acoustic correlation sonar for vertical profilingof ocean currents to a rangeof 1km[C]∥IEE Proc.Radar,Sonar and Navigation.1996,143(3):177-183.

[14] 冯 雷,王长红,汪玉玲,等.相关测速声纳工作原理及海试验证[J].声学技术,2005,24(2):70-75.

[15] R N Bracewell.Radio astronomy techniques[J].Handbuch der physik,1962,54:42-129.

A design method of arrays for acoustic correlation logs

XUEJing-hong,JIN Ming,QIAO Xiao-lin
(Institute of Information Engineering,Harbin Institute of Technology atWeihai,Weihai 264209,China)

TB56

A

1005-9865(2011)01-0130-05

2010-06-11

薛敬宏(1974-),男,山东胶南人,副教授,博士,主要从事水声数字信号处理、深海测速技术研究。E-mail:xjh@hitwh.edu.cn