二维饱和多孔介质因点汇诱发比奥固结的解析解
李培超
(上海工程技术大学 机械工程学院,上海 201620)
1 引 言
众所周知,Biot首次推导建立了较为严格和完整的饱和土体三维固结理论[1-2],从而奠定了多孔介质流-固耦合渗流理论的基础。Biot固结理论从提出至今,已被广大岩土力学工作者所接受,它在很多工程领域都有广泛地应用,如软土地基固结沉降、地下流体开采诱发地面沉降、边坡稳定性问题、城市垃圾填埋及核废料处理、煤层气的耦合渗流和突出、生物体软组织变形等领域。
因点源汇诱发的土体固结问题的解析解,目前已有不少文献报道[3-5],但它们绝大多数都是针对三维区域(如半空间)或无限区域的。文献[6]首次给出了二维有限矩形区域点汇诱发的流动变形耦合问题的解析解。但所采用的数学模型是不可压缩多孔介质模型,本文则尝试给出二维有限区域可压缩多孔介质模型的解析解。
2 数学模型
2.1 控制方程组
考察二维有限矩形区域内因点汇(源)诱发的Biot固结问题,物理模型如图1所示,该问题可视为平面应变问题。假设多孔介质被单相流体所完全饱和,且是均匀各向同性和线弹性的,此时Biot固结理论(或称可压缩多孔介质模型)可简化为
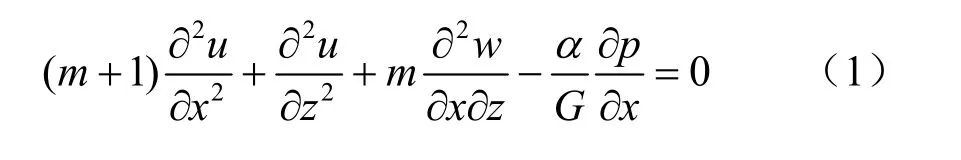
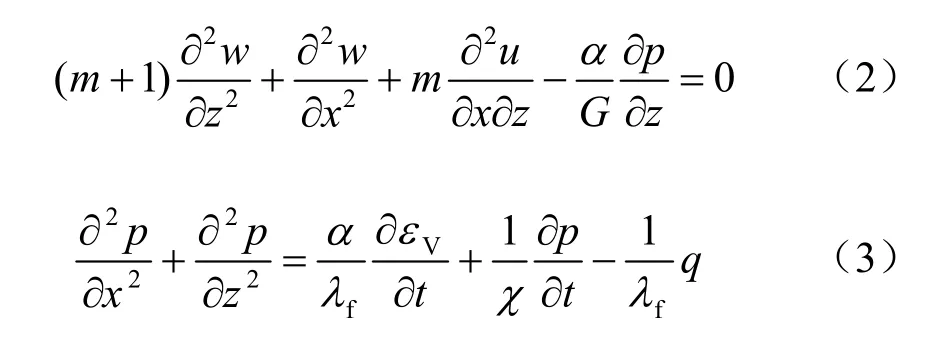
式中:p为孔隙流体压力;u和w分别为水平方向和竖直方向的位移;α =1- Kb/Ks,为Biot孔隙弹性系数,Kb为多孔介质体积弹性模量,Ks为固体颗粒体积弹性模量;λf= k/μf是孔隙流体流度,k为绝对渗透率,μf为孔隙流体黏度;φCt= φ/ Kf+ (α - φ)/Ks,φ为多孔介质孔隙度,Ct为总体压缩系数,Kf为孔隙流体体积弹性模量;χ=λf/(φCt)为导压系数; m = 1/(1 - 2v),v为多孔介质泊松比;G为剪切体积弹性模量为体积应变;q代表单位体积的源(源取正,汇取负),量纲为1/s。
如果不考虑多孔介质固体颗粒和孔隙流体的压缩性,即Ks→∞,Kf→∞,则α→1,1/χ→0,此时式(1)~(3)退化为
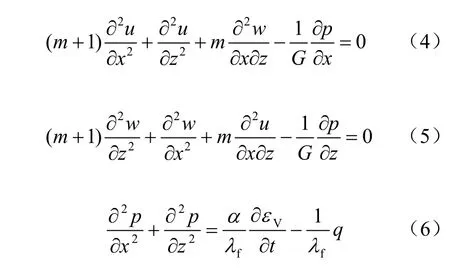
方程组(4)~(6)显然即是文献[6]所采用的不可压缩多孔介质模型。
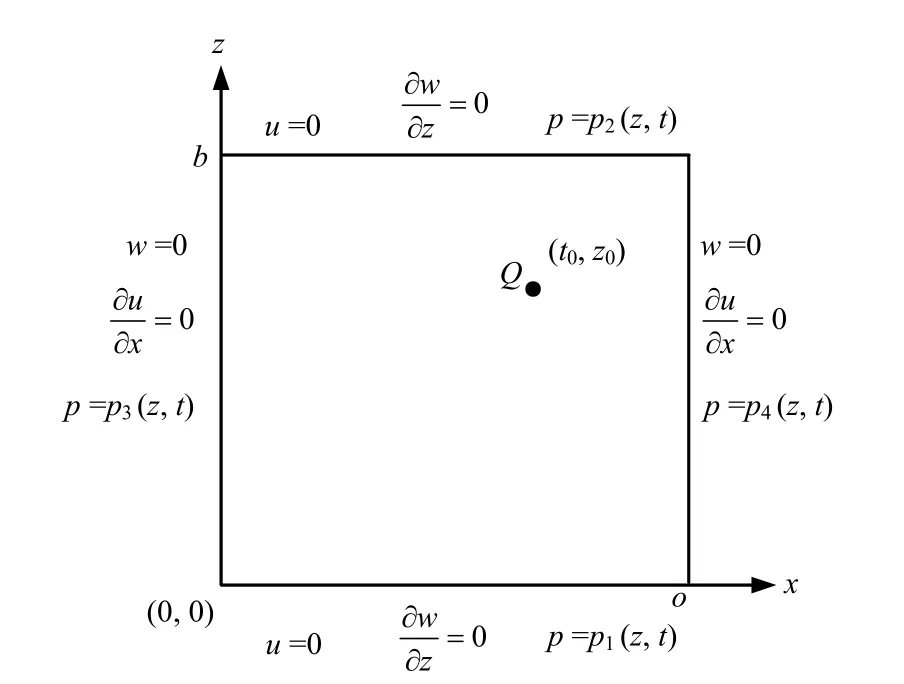
图1 二维有限矩形多孔介质示意图[6]Fig.1 Sketch of finite two-dimensional rectangular porous media[6]
2.2 边界条件和初始条件
为简单起见,本文假设压力场和位移场边界条件与文献[6]完全相同,如图1矩形四条边所示。同时假设初始条件为 u(x,z,t = 0)= 0,w(x,z,t = 0)=0,和 p(x,z,t = 0)= 0。控制方程组(1)~(3)与边界条件和初始条件构成了封闭的定解问题。下文试图给出该定解问题的解析解。
3 积分变换和求解
3.1 积分变换和变换域上的解析解
对于上述平面应变固结问题,可实施有限正余弦变换和拉氏变换求其解析解。相应变换定义[6]为
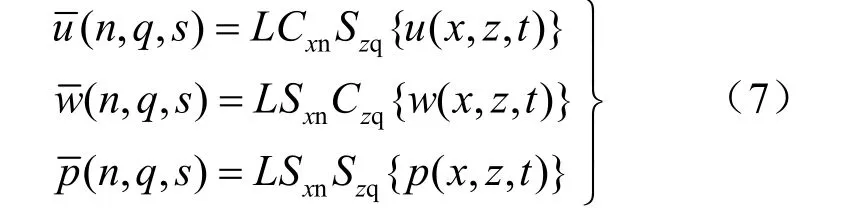
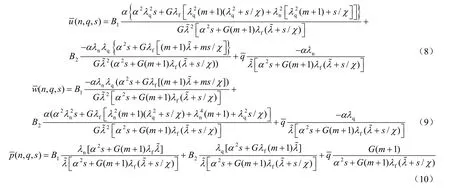
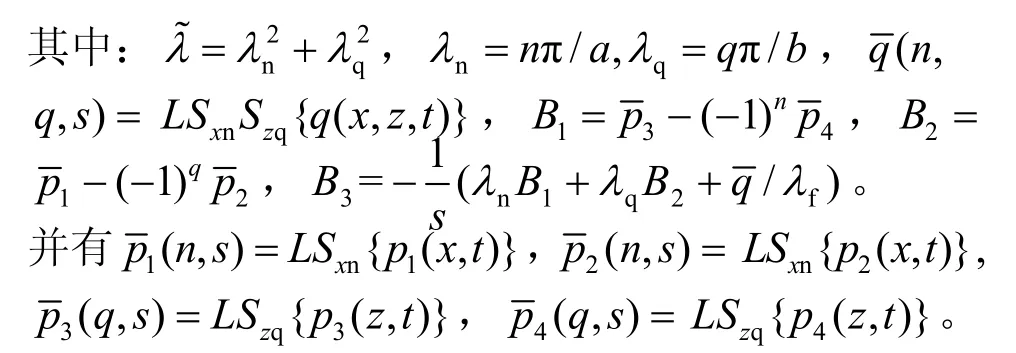
式(8)~(10)即是可压缩多孔介质模型在变换域上的解析解。可见以上解答中包含参数α及χ,即体现了Biot孔隙弹性系数以及多孔介质压缩性的影响,而这些因素在不可压缩模型的解析解[6](即文献[6]之式(19))中是根本无法反映的。
对于不可压缩多孔介质模型,有α→1,和1/χ→ 0 ,式(8)~(10)简化为
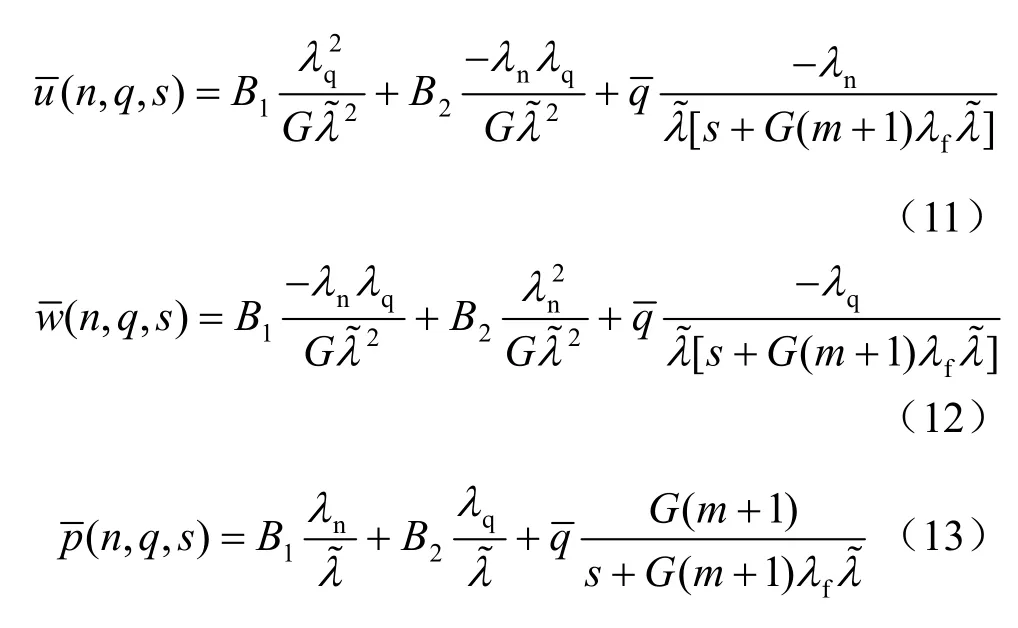
上述简化解式(11)~(13)和文献[6]之式(19)相似。前者是有量纲形式,而后者是无量纲形式。不难证明,如果虑及二者之换算关系,实际上此二解是完全相同的。这一方面证实了不可压缩多孔介质模型之解析解可视为本文解析解的特例,同时也在一定程度上验证了本文解析解的正确性。
3.2 物理域之解析解
对式(8)~(10)实施三重反演可得二维有限区域平面固结问题的解析解如下:
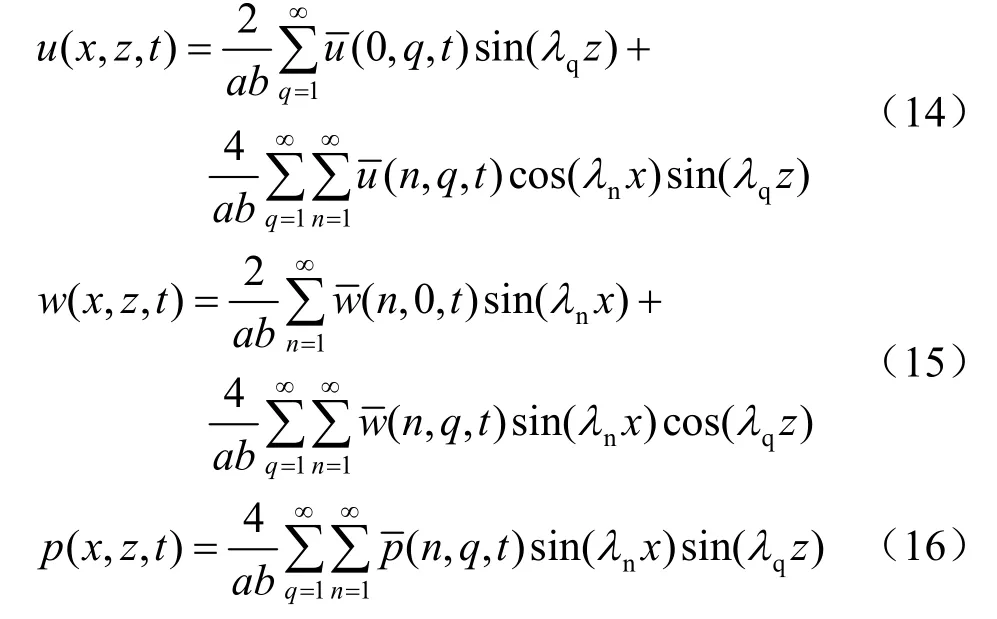
4 定流量点汇(源)问题的解析解及验证
4.1 定流量点汇(源)的解析解
不妨假设矩形区域边界压力满足 p1=p2=p3=p4=0,则有 B1=B2= 0。另假设源(汇)流量为 常 数 , 即 q(x,z,t)= q0δ ( x - x0)δ(z - z0), 则将B1、B2及上述值代入式(8)~(10),并实施拉普拉斯反演,得
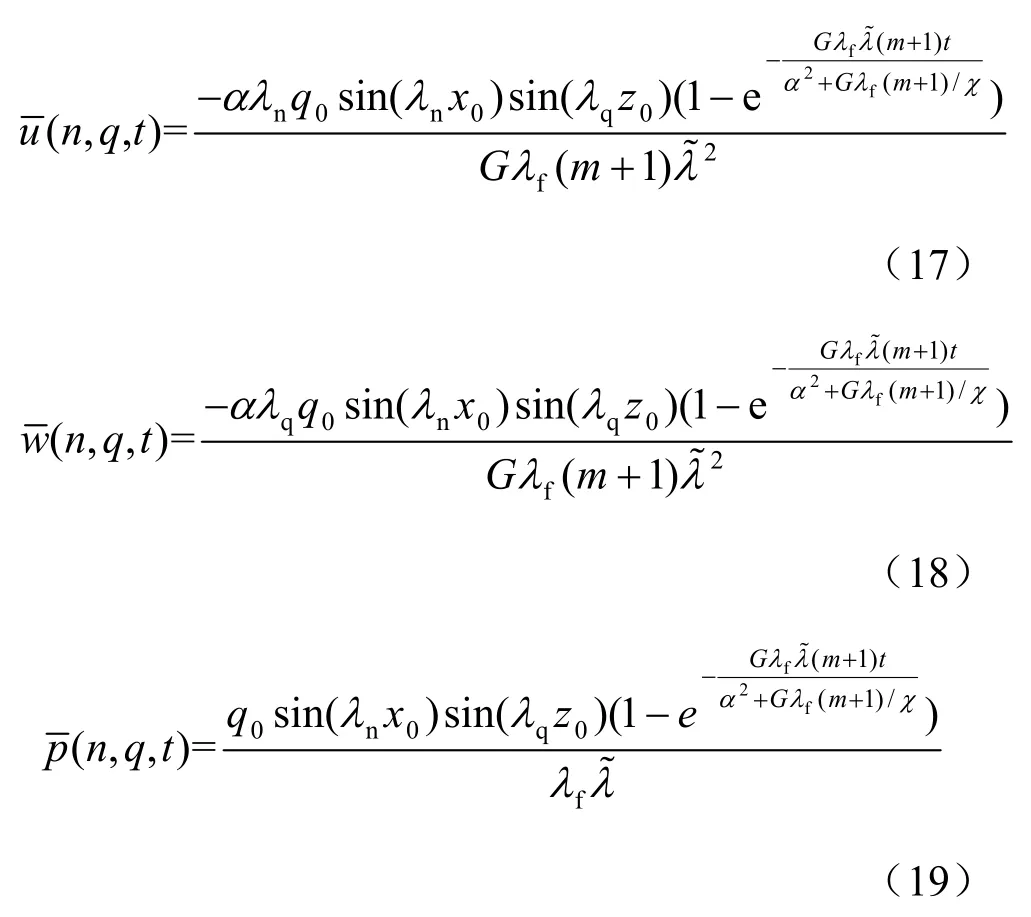
将式(17)~(19)代入式(14)~(16),即得定流量点源(汇)诱发的位移场和压力场在物理空间上的解析解。
4.2 稳态解析解的验证
当t趋于无穷时的解通常称为稳态解。当t趋于无穷时,对式(17)~(19)进行简化并代入式(14)~(16),可得稳态解为

文献[7]给出的压力稳态解析解为
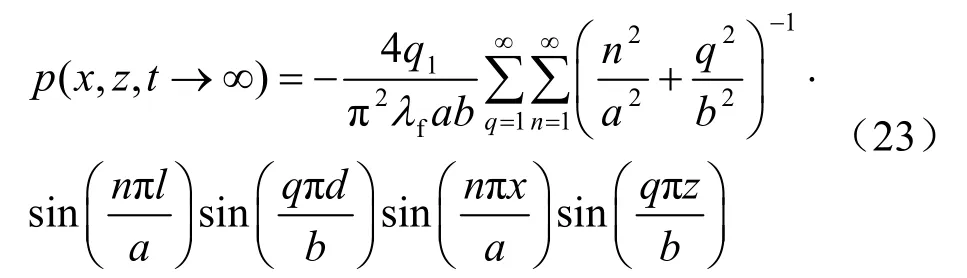
其中:q1为定流量汇(正值)。
对于点汇,有 q0=-q1,又虑及 λn= nπ/a,则式(22)可改写为
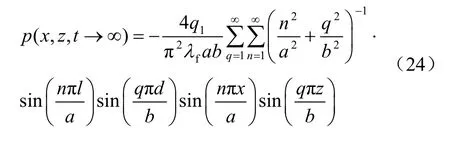
可见,式(24)与式(23)完全相同,这再次验证了本文解析解之准确性。而且此处同时给出了位移场的稳态解析解,即式(20)和式(21)。
5 结 语
本文给出了有限二维区域因点汇诱发的Biot固结问题的解析解。结果表明,不可压缩多孔介质模型的解析解是本文解析解的特例。并进一步讨论分析了定流量汇所诱导的压力场和位移场之稳态解析解,它与现有文献解析解的完全一致性再次验证了本文解析解的准确性和可靠性。
[1]BIOT M A. General theory of three-dimensional consolidation[J]. J. Appl. Phys., 1941, 12: 155-164.
[2]BIOT M A, WILLIS D G. The elastic coefficients of the theory of consolidation[J]. J. Appl. Mech., 1957, 24: 594-601.
[3]BOOKER J R, CARTER J P. Analysis of a point sink embedded in a porous elastic half space[J]. Int. J. Numer.Anal. Meth. Geomech., 1986, 10(2): 137-150.
[4]TARN J Q, LU C C. Analysis of subsidence due to a point sink in an anisotropic porous elastic half space[J].Int. J. Numer. Anal. Meth. Geomech., 1991, 15(8): 573-592.
[5]CHEN G J. Analysis of pumping in multilayered and poroelastic half space[J]. Computers and Geotechnics,2003, 30: 1-26.
[6]BARRY S I, MERCER G N. Exact solutions for two dimensional time dependent flow and deformation within a poroelastic medium[J]. J. Appl. Mech., 1999, 66: 536-540.
[7]孔祥言. 高等渗流力学(第二版)[M]. 合肥: 中国科学技术大学出版社, 2010.

