斜边非轴对称位移边界下球孔扩张挤土分析

饶平平 ，李镜培 ，刘 颖

（1. 同济大学 岩土及地下工程教育部重点实验室，上海 200092；2. 同济大学 地下建筑与工程系，上海 200092；3. 南昌工程学院 土木与建筑工程学院，南昌 330099）

1 引 言

近年来，国内外学者及工程技术人员对沉桩挤土所带来周围环境的不利影响进行了大量的研究，取得了显著的研究成果[1－6]。然而，目前针对该问题的研究主要是基于平面应变轴对称假定的基础上，应用圆孔扩张法、应变路径法以及有限元等方法分析，实际工程中很多施工场地所处的环境存在非轴对称位移边界，例如：①为避免沉桩对周围环境（包括地下管线、已有建筑物基础、道路等）的影响，在施工场地和已有建（构）筑物之间修隔离墙、开挖隔离槽、设置应力释放孔和预钻孔等，形成非轴对称位移边界条件[7]；②施工场地本来存在非轴对称位移边界条件，如施工场地靠近斜坡（边坡）或码头岸坡问题。

非轴对称位移边界条件下沉桩扩孔所造成的挤土效应，对于这一问题目前尚缺乏充分地研究，没有成熟的计算方法，对其挤土效应机制也不是很清楚。我国上海的白莲泾河在堤岸加固过程中，沉桩时岸坡发生严重的变形以及不同程度的裂缝[8]；浙江舟山20×104t油码头系缆墩，沉桩时产生了1 m多的位移，最后码头岸坡发生大滑坡，使得一个系缆墩全部滑入海中，损失惨重[9]。文献[7]应用曲线坐标变换方法，试图研究非轴对称位移边界下圆孔扩张问题，但其只能求解固定边界条件下的应力场及位移场，且解析过程较为繁琐；文献[10]采用位移-位移问题的假定，从球孔扩张的基本解答出发，得到了水平自由位移边界条件下的位移场，然而，实际工程大多数边界不仅是水平自由位移边界，而是存在不同倾斜角度。基于以上原因，本文针对现有球孔扩张理论的不足，对球孔扩张进行改进，采用镜像方法，通过对地表边界以及倾斜边界应力的修正，得到了非轴对称位移边界下的球孔扩张挤土位移解答，并进行参数影响分析。

2 基本理论及力学模型

沉桩挤土位移问题可以采用平面应变假定的柱孔扩张法和无限土体假定的球孔扩张法模拟，但这些解答不能很好地反映沉桩挤土位移场的半无限空间特性，半无限空间和无限空间问题相比，增加了地表的自由边界，因此，需要满足地表边界处竖向应力及剪应力同时为 0。针对本文研究的斜边非轴对称位移边界下半无限球孔扩张问题，作如下基本假定：①土体为均质线弹性体，满足虎克定律；②土体变形为小变形；③忽略土体的自重作用；④土体饱和，不可压缩，且土体变形为位移-位移问题。

由于水平向位移边界对水平及竖向位移影响较大，而对y方向的位移影响较小，因此，本文主要对水平及竖直方向位移进行分析。如图1所示，在半无限土体内半径为a的球孔扩张，球孔坐标为（0，0，h），在x=t处的位置存在水平自由位移边界。假定边界面光滑，根据对称镜像原理，在对应于自由位移边界处的位置设置镜像收缩球孔，R1为孔周任意一点 p(x, 0,z)到球孔中心的距离，R2为孔周一点 p(x, 0,z)到镜像收缩球孔中心的距离，空间柱坐标系下可以得到球孔扩张后孔周任意一点p(x, 0,z)处的挤土位移场[10]：

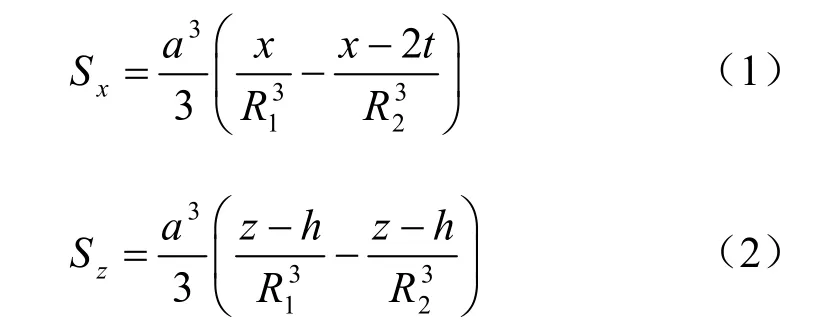
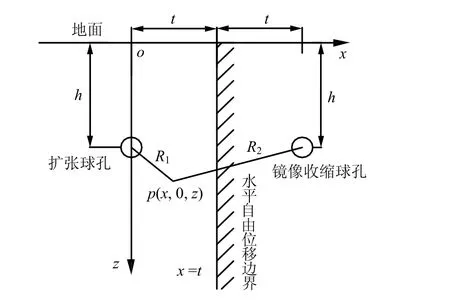
图1 水平自由位移边界示意图Fig.1 The sketch of horizontal displacement boundary

3 非轴对称边界球孔扩张位移求解

3.1 非轴对称边界下无限土体球孔扩张位移解答

具有一定倾斜角度的非轴对称位移边界条件下球孔扩张如图 2所示，在距离坐标原点t处的位置存在一定坡度的自由位移边界，斜面自由边界倾斜角为ϕ，同样在相对应斜面边界镜像位置设置镜像收缩球孔，R1为孔周任意一点 p(x, 0,z)到球孔中心的距离，R3为孔周一点 p(x, 0,z)到镜像收缩球孔中心的距离。

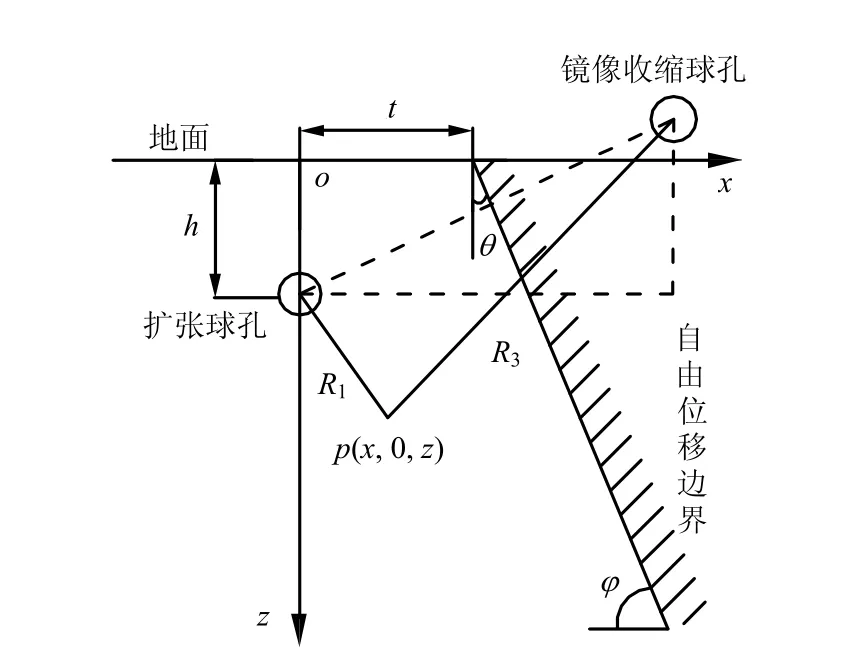
图2 非轴对称位移边界扩孔示意图Fig.2 The sketch of cavity expansion with nonaxisymmetric displacement boundary

由图3可知，R3的表达式与h、t和θ三者的关系有关，根据图中几何关系可以得到：

①当镜像收缩孔位于地表面以上时，如图3(a)所示，即 h＞tt an2θ情况下。

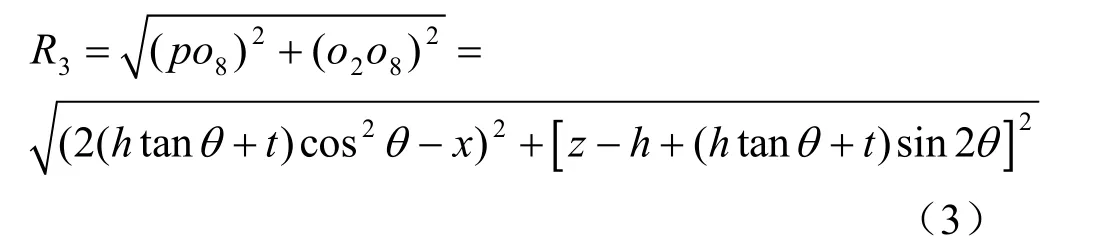
②当镜像收缩孔位于地表面以下时，如图3(b)所示，即 h＜tt an2θ情况下。

同理可得R3的表达式为

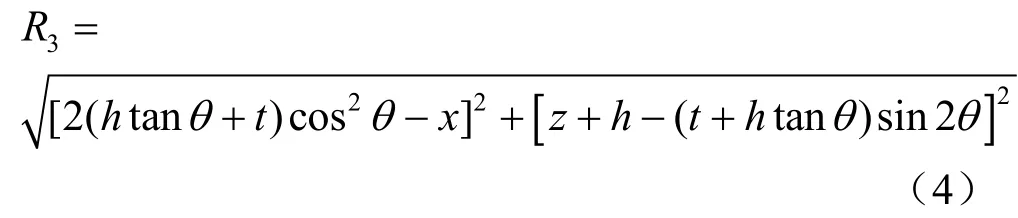
③当镜像收缩孔刚好位于地表面时，如图3(c)所示，即 h=tt an2θ情况下。

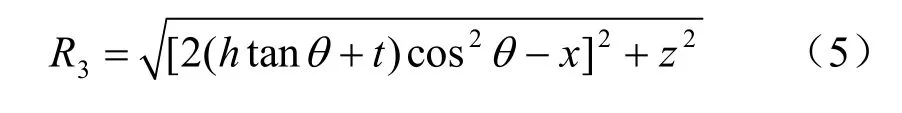
式中：θ为斜面边界与竖直方向的夹角，θ=90°-ϕ。

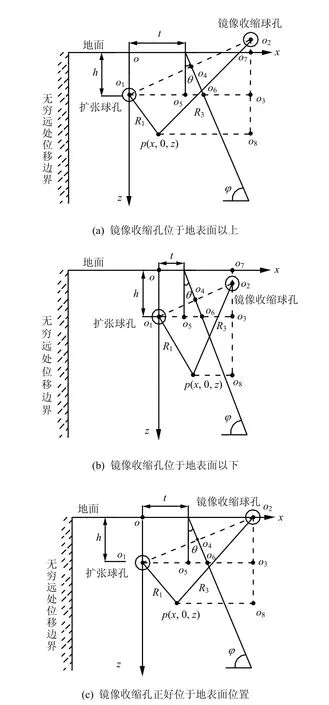
图3 非轴对称位移边界扩孔示意图Fig.3 The sketch of spherical cavity expansion with nonaxisymmetric displacement boundary

同理可得具有一定倾斜角度的非轴对称位移边界条件下球孔扩张后孔周任意一点 p(x, 0,z)处的挤土位移表达式为

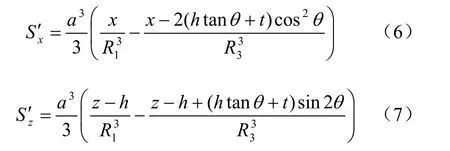
当θ=0°时，式(6)、(7)可以退化到式(1)、(2)，即文献[10]解答，当θ=90°时，式(6)、(7)可以退化为文献[11]的解答。

土体应变可根据弹性力学几何方程得到：

式中：εx与εz为土体x与z轴方向应变；γxz为剪应变。

3.2 地表边界应力修正

上述3.1节非轴对称位移边界球孔挤土位移表达式是基于无限土体空间的假定而得到的，为反映扩孔挤土位移场的半无限空间特性，有必要对地表自由边界以及倾斜边界应力进行修正，修正后需要满足的边界条件为：地表以及倾斜边界竖向应力与剪应力同时为0。

对于地表应力边界而言，可以分成两种情况来讨论，分别采用不同的应力函数解答来分析：

对于满足情况①的边界条件弹性力学问题，可以采用以下应力函数解答来求解[12]：

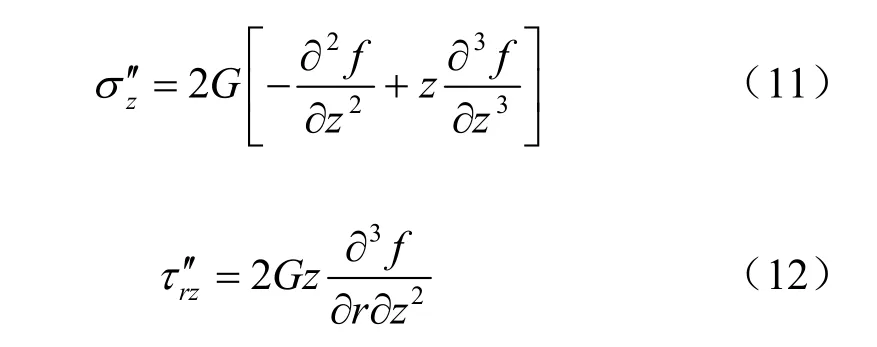
式中：f为应力修正函数；G为土体剪切模量。

相应的位移为

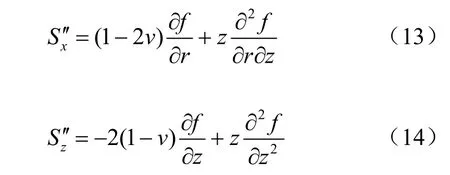
式中： v 为土体泊松比， Sx′、 Sz′为修正竖向应力产生的水平及竖向位移。

对于满足情况②的边界条件弹性力学问题，可以采用以下应力函数解答来求解[12]：

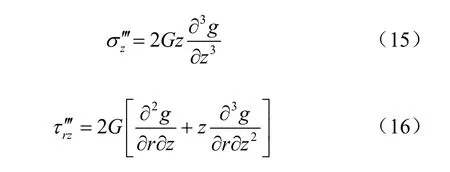
式中：g为应力修正函数。

相应的位移为

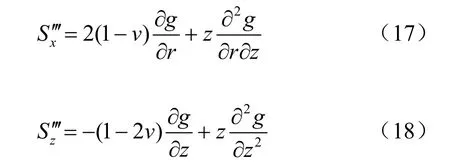
式中： Sx′、 Sz′为修正剪应力的水平及竖向位移。

取修正应力函数为

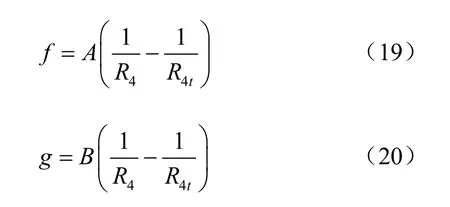
式中：A、B为待定常数；R4与R4t是由边界条件而得到的修正函数表达式，其中R4为球孔(真实源)关于地表面对称位置到 p(x, 0,z)点的距离，为镜像收缩孔(镜像汇)关于水平地表面对称位置到 p(x, 0,z)点的距离，同理，R4t的表达式也需根据具体情况而定，具体如下：

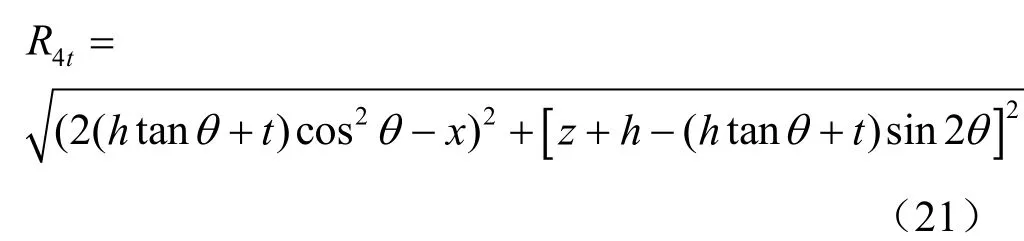
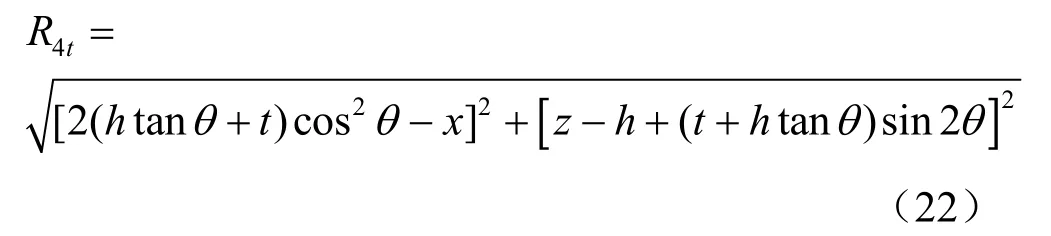
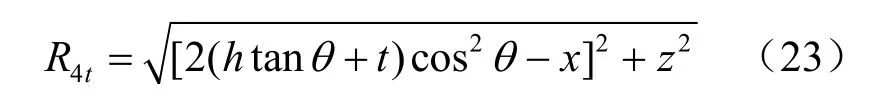
函数 f、g的表达式满足∇2f=0，∇2g=0，根据式(6)、(7)可得在边界z=0处的竖向应力和剪应力分别为

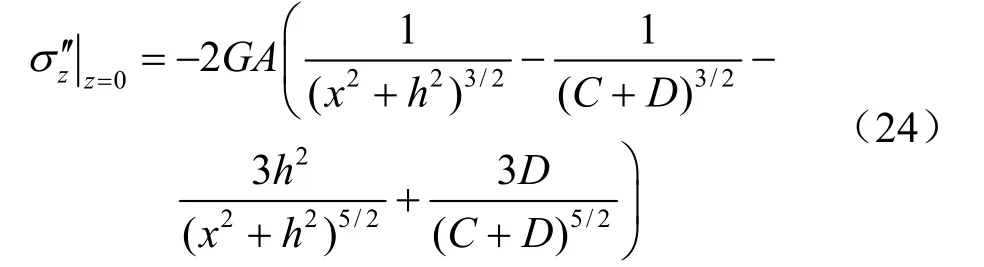
又由于

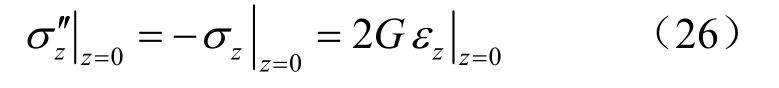
将式(9)代入式(26)中，结合式(24)及式(26)可得：

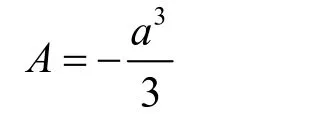
将A，B表达式代入修正应力函数后，再代入位移解答中，可得修正竖向应力产生的位移为

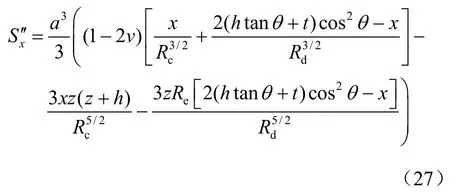
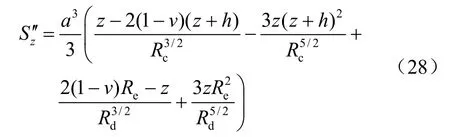
式中： Rc= x2+ (z +h)2

当 h＞tt an2θ时，

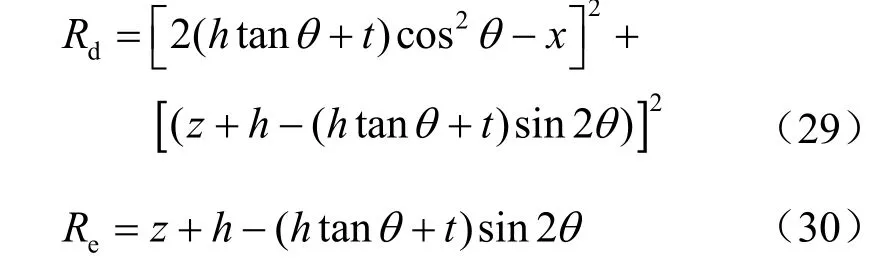
当 h ≤ tt an2θ时：

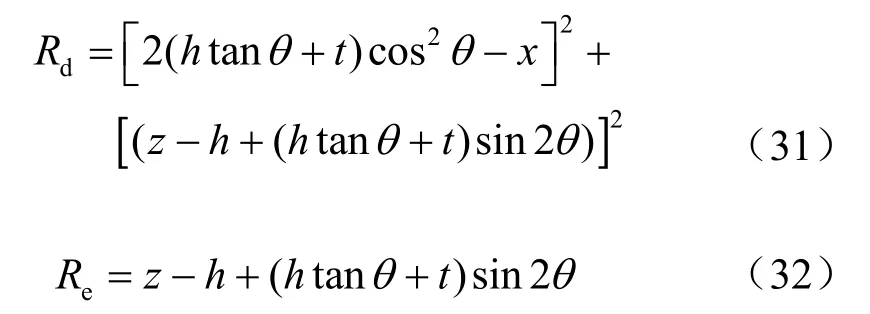
同理，可得修正剪应力产生的位移为

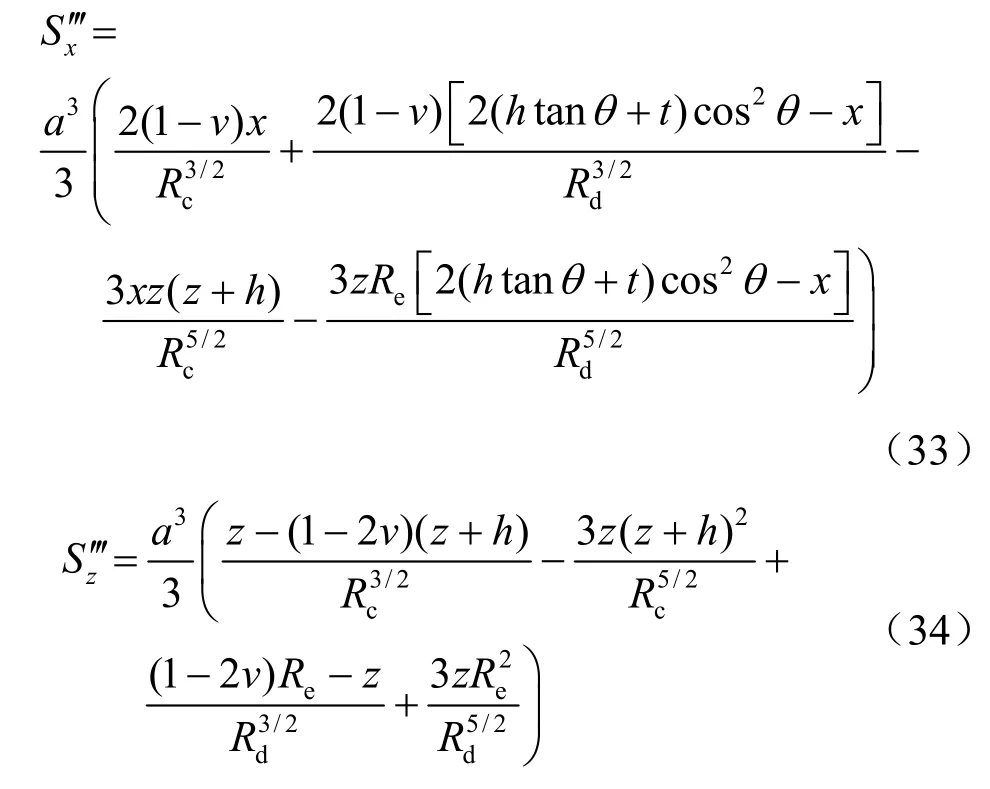
3.3 斜面自由边界应力修正

如图2所示，真实源与镜像汇共同作用下在斜面边界上产生了一个附加剪应力τxz，为了消除剪应力的影响，需要一个与之大小相等，方向相反的剪应力-τxz来平衡，以恢复斜面边界表面无约束的情况，由于弹塑性情况下很难求出其解析解，因此，假定土体是线弹性材料，则由式(6)、(7)可得到剪应变：

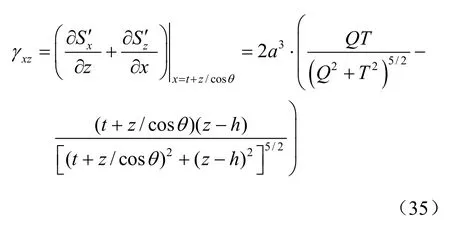
式中：γxz为斜面边界上的剪应变； Q=[t +z/cosθ - 2(h tan θ+ t )cos2θ]； T = [z - h + (h tan θ+t)sin2θ]。

故相应的剪应力为

根据Cerruti解答可得斜面边界上的剪应力-τxz作用下球孔周围产生的位移场：

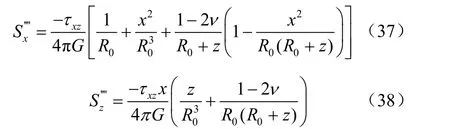
结合式(35)～(38)即可得到斜面边界上修正的剪应力对土体产生的位移场。

根据上述推导，可得到地表面以及斜面自由边界应力修正后的非轴对称位移边界条件下球孔扩张土体位移解答：

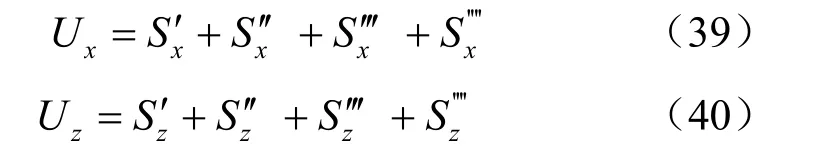
3.4 对本文解答的讨论

本文推导的解答为斜边非轴对称位移边界条件下球孔扩张挤土位移解答。由于文献[10]推导的非轴对称位移边界下球孔扩张位移解答仅能适用于θ=0°情况下，且并未对非轴对称边界上产生的剪应力进行修正，因此，文献[10]得到的只是近似意义上的解答，令θ=0°，式(39)中的前三项可以退化到文献[10]的解答。本文解答中，令θ=90°，则式(39)、(40)可退化到轴对称位移边界条件下半无限土体扩孔解答，即文献[11]的解答。因此，文献[10]、[11]中解答仅为本文解答的一个特解，本文解答除可以考虑球孔离边界不同距离、不同孔径大小的挤土位移外，还可考虑边界的不同倾斜角度对应的位移变化规律。

另外，由本文解答的推导过程可以看出，地表面自由边界处的正应力及剪应力均被修正；由于真实源与镜像汇相互作用后，斜面边界的正应力为0，不需修正，斜面自由边界的剪应力也通过 Cerruti解答得到了修正，因此，本文方法得到的位移解可为非轴对称位移边界条件下球孔扩张后位移分析提供理论基础。如将单个球孔扩张挤土位移扩展至一系列球孔扩张便可得到非轴对称位移边界条件下单桩沉桩的挤土位移解答，该解答对预估邻近斜坡、岸坡等条件下沉桩产生的挤土位移具有一定的参考和现实意义。

4 分析与讨论

由于能考虑自由边界角度θ的变化对挤土位移的影响是本文解答的特色及创新之处，同时边界角度θ也是影响邻近基坑斜坡、边坡及码头岸坡等非轴对称位移边界条件下挤土位移的重要因素之一，故本文将重点分析参数θ及参数θ与其他不同因素的组合对挤土位移的影响。为分析各具体因素对解析解的影响规律及敏感性，假定泊松比ν=0.5，在其他参数保持不变的前提下，只使一个因素在一定范围内变化。

4.1 θ 对挤土位移的影响

不同边界角度θ对孔周挤土位移的影响如图 4所示，为准确分析θ变化对挤土效应的影响，令挤土总位移由图4(a)可以看出，在球孔深度范围内，水平挤土位移及总位移随着深度的增大而逐渐增大，且在球孔所处深度位置的挤土位移最大，此后随着深度的增大而逐渐减小；当边界角度θ=0°时，即竖直自由边界情况下，靠近自由边界一侧的最大水平挤土位移为35.3 mm，最大总位移为36.4 mm，受位移边界非轴对称因素的影响，远离自由边界一侧相同距离位置处的最大水平位移为23.0 mm，最大总位移为23.6 mm，仅为靠近自由边界一侧位移的 65.2%和 64.8%，因此，在实际工程中应充分重视非轴对称位移边界的影响。

随着θ角度的不断增大，靠近自由边界一侧的水平位移及总位移逐渐减小，当θ=15°，最大水平挤土位移减小至 26.8 mm，最大总位移减小至27.4 mm；当θ=90°，模型退化为半无限土体空间下球孔扩张问题，此时最大水平位移为 24.8mm，最大总位移为 25.5 mm。也就是说，θ=15°、90°比θ=0°时水平位移以及总位移分别减小了24.1%、29.7%和24.7%、29.9%，说明θ越大，θ角度对位移的影响幅度越小。对于远离自由边界一侧挤土位移而言，θ=15°、90°比θ=0°时水平位移以及总位移分别增大了3.5%、7.8%和3.8%、8.1%，也就是说，挤土位移随着θ的增大而增大，但θ角度变化对其影响幅度不大。

图4较好地解释了在实际邻近斜坡沉桩扩孔工程中自由边界倾斜越陡(即参数θ越小)，斜坡挤土位移越大，相应地斜坡稳定性也越差。但需要注意的是，在实际工程应用中，如斜坡较陡需要削坡时，在确保斜坡安全和经济的前提下，应根据工程实际情况和斜坡允许的最大挤土位移，合理确定边界倾斜角度。

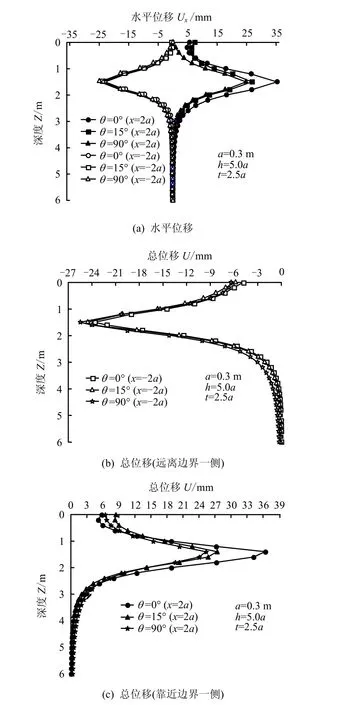
图4 不同θ 对挤土位移的影响Fig.4 The influence of θ on the displacement

4.2 t 对挤土位移的影响

球孔离边界不同距离t对挤土位移的影响如图5所示，可以看出，对于靠近自由边界一侧而言，随着t值的增大，相同位置的水平位移逐渐减小，且 t值的不断增大对水平位移的影响幅度逐渐减小，如当θ=0°时，t=4a、t=5a所对应的水平位移分别比t=3a减小51.7%和71.8%；另外，t值的改变对远离自由边界一侧位移影响规律与靠近自由边界一侧相同，但相同条件下远离自由边界一侧水平位移值比靠近自由边界一侧要小。图5从理论上解释了邻近斜坡扩孔工程中，球孔离斜坡越近，扩孔后其挤土位移越大。

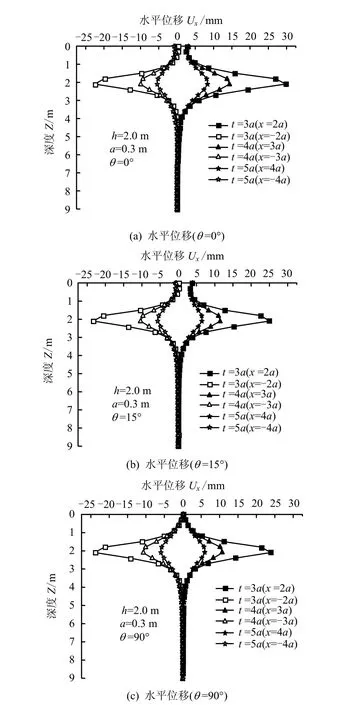
图5 不同θ 下t对挤土位移的影响Fig.5 The influence of t on the displacement with different values of θ

5 结论及展望

（1）本文所得解答不仅适用于具有不同自由边界倾斜角度的非轴对称位移边界条件下的球孔扩张，还可以退化为轴对称位移边界条件下球孔扩张位移解答，具有广泛的实用性，可为类似工程挤土位移控制及参数设置提供参考。

（2）随着边界角度θ的不断增大，靠近自由边界一侧的挤土位移逐渐减小，但对远离自由边界一侧球孔挤土位移影响不大，该结论较好地解释了在实际邻近斜坡沉桩扩孔工程中，自由倾斜边界越陡(即参数θ越小)，斜坡挤土位移越大，相应地斜坡稳定性也越差。

（3）对于靠近自由边界一侧而言，随着球孔离边界不同距离的增大，相同位置的挤土位移逐渐减小。因此，在实际工程应用中，应根据工程实际情况和斜坡允许的最大挤土位移，合理确定球孔与斜坡倾斜表面的距离。

[1]VESIC A S. Expansion of cavities in infinite soil mass[J].Journal of the Soil Mechanics and Foundations Division, ASCE, 1972, 98(3): 265－290.

[2]BALIGH M M. Strain path method[J]. Journal of Geotechnical Engineering, 1985, 111(9): 1108－1136.

[3]CAO L F, THE C I, CHANG M F. Undrained cavity expansion in modified Cam clay[J]. Geotechnique, 2001,51(4): 323－334.

[4]COLLINS I F, YU H S. Undrained cavity expansion in critical-state soils[J]. International Journal for Numerical and Analytical Methods in Geomechanics,1996, 20: 489－516.

[5]SALGADO R, MITCHELL J K, JAMIOLKOWSKI M.Cavity expansion and penetration resistance in sand[J].Journal of Geotechnical and Geoenvironmental Engineering, 1997, 123(4): 344－354.

[6]SAGASETA C, WHITTLE A J. Prediction of ground movements due to pile driving in clay[J]. Journal of Geotechnical and Geoenvironmental Engineering,2001, 127(1): 55－66.

[7]高子坤, 施建勇. 基于非轴对称位移边界的沉桩挤土圆孔扩张解研究[J]. 土木工程学报, 2007, 40(增刊):344－349.GAO Zi-kun, SHI Jian-yong. Research of non-symmetric CEM and pile-sinking induced soil squeezing effect[J].China Civil Engineering Journal, 2007, 40(Supp.): 344－349.

[8]SHEN Shui-long, HAN Jie, ZHU He-hua, et al.Evaluation of a dike damaged by pile driving in soft clay[J]. Journal of Performance of Constructed Facilities, 2005, 19(4): 300－307.

[9]魏汝龙, 张诚厚. 提高码头岸坡稳定性的经验总结[C]//第三届岩土工程论文集. [S. l.]: [s. n.], 1981: 445－451.

[10]朱宁. 静力压桩引起桩周土体变形的理论分析[D]. 南京: 河海大学, 2005.

[11]SAGASETA C. Analysis of undrained soil deformation due to ground loss[J]. Geotechuique, 1987, 37(3): 301－320.

[12]KASSIR M K, SIH G C. Three-dimensional crack problems[M]. Dordrecht: Noordhoff International Publishing, 1975.

[13]罗战友. 静压桩挤土效应及施工措施研究[D]. 杭州:浙江大学, 2004.