非均质地基中平面应变隧道开挖面稳定上限分析
宋春霞 ,黄茂松 ,吕玺琳
(1. 同济大学 地下建筑与工程系,上海 200092;2. 同济大学 岩土及地下工程教育部重点实验室,上海 200092)
1 引 言
在隧道开挖施工中土体相当于水平卸载,开挖面前方土体将形成一个三维松动区域,需在开挖面施加支护压力才能防止土体向内发生松动而失稳。盾构施工中,开挖面的稳定是通过压力舱(加气、加泥水)施加支护压力得以实现的。压力舱支护压力较小时会出现地基沉降甚至坍塌,开挖面支护压力过大会造成地表隆起[1]。因此,合理地确定开挖面支护压力是盾构掘进施工中一项关键技术,目前,开挖面稳定研究中大部分侧重于开挖面极限支护压力的确定。
浅埋隧道开挖后易形成贯穿地表的滑动面,产生较大范围的塑性流动区域,所以隧道开挖面稳定是一个三维问题。目前,国内外已有许多学者用模型试验[3]及数值计算分析[4-5]对其进行了研究,分析了开挖面失稳破坏模式。并有许多学者基于其成果陆续提出了平面应变的简化模型和计算方法:Eisenstein和Samarasekara[6]采用极限平衡和位移有限元相结合的方法研究了黏土中隧道的稳定问题;Anagnostou和Kovari[7]亦采用了极限平衡法考察了排水条件下隧道稳定所需要的支护压力。也有学者将极限分析理论初步应用于隧道开挖面稳定性分析中。Atkinson和Potts[8]利用模型试验和极限分析上限法和下限法研究了无黏性土浅埋隧道稳定性问题。Davis等[9]针对黏性土不排水条件下浅埋隧道,假定3种不同的破坏模式,利用极限分析理论上下限原理对隧道工作面失稳及局部破坏现象进行了分析,并得到了相应的模式下稳定系数关于隧道埋深的解答。Leca和 Dormieux[10]针对砂性土地基中的环形隧道构造了含刚性锥体滑块的破坏模式,研究了浅埋隧道工作面的三维稳定性问题。Sloan等[11]是以极限分析有限元法研究了隧道在均质地基中不排水条件下的支护压力的上下限值,大大改善了已有的计算结果,给出了荷载参数的表格形式以供工程师们参考查阅。以上作者考虑隧道开挖面稳定时,均假定地基土抗剪强度是均匀的,事实上K0固结黏土层土体不排水抗剪强度与上覆有效应力有关,即随深度呈线性变化,所以其研究成果适用范围有限。Sloan和 Assadi[12]采用极限分析有限元法考察了非均质地基中方形隧道开挖面支护压力上下限解,并以简单的刚性块体得到的上限解进行比较验证;Augarde等[13]以极限分析有限元法,得到了非均质地基中平面应变隧道支护压力的上下限解,指出在非均质地基中以稳定系数N来评价隧道开挖面稳定性是不恰当的。但他们都没有考察开挖面破坏时对周围地基变形的影响及其范围。
本文针对纯黏土材料,基于极限分析上限法,考虑土体剪切强度随深度线性变化,采用刚性多块体平移滑动破坏模式来探讨不排水条件下,隧道开挖面极限支护压力的上限解,为实际工程中确定隧道盾构施工中的支护压力提供了一个简单可靠的理论依据。
2 平面应变隧道开挖面的破坏模式
图1为简化的平面应变隧道(plane strain heading)力学模型,隧道直径为D,埋深为C(隧道顶面到地平面的距离)。地表承受均布荷载σS,为保持隧道开挖面稳定,开挖面作用均布压缩气体或其他液体压力σT。地基土重度为γ,在外荷载作用下不排水强度随深度呈线性变化:
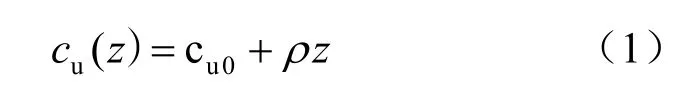
式中:cu(z)为深度z处的不排水强度;cu0为地基表面处不排水强度;ρ为不排水强度随深度变化率。
当ρ=0时, cu(z)=cu0,地基为均质土体;当cu0=0时,cu(z)=ρz,对应于正常固结沉积土。本文中所考虑的问题则对应于ρ>0而且cu0>0的情况,即剪切强度值在地基表面为定值,随深度线性变化。
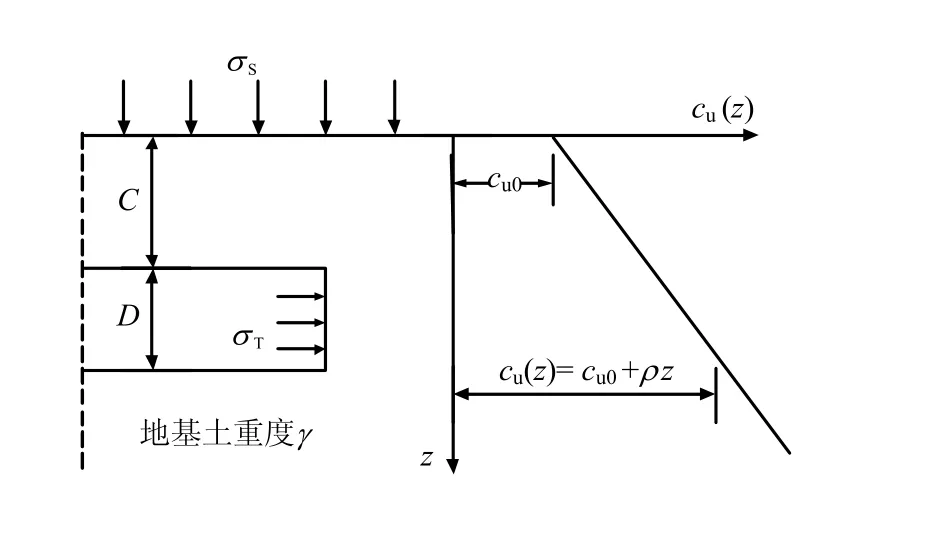
图1 平面应变隧道开挖面Fig.1 Plane strain excavation face of tunnel
隧道开挖的稳定问题是:在隧道埋深以及土体力学性质一定的情况下,隧道开挖面至少需要施加多大的支护压力σT才能防止塌方。这里采用塑性极限分析上限法来探讨平面应变隧道开挖面稳定极限支护压力的计算。影响隧道开挖面稳定的因素很多,本文仅考虑地表面水平,并简化为平面应变问题,作以下假定:
(1)三维隧道被假定为图 1所示平面应变情况;(2)假定隧道开挖面作用轴向支护压力沿竖向均匀分布(实际上隧道顶部和底部压力分布不同);(3)隧道周围土体为纯黏土处于不排水条件,假定为理想弹塑性体,服从Tresca屈服准则;(4)隧道变形模式允许隧道上部和前方土体向隧道内塌陷。
极限分析上限法中通常的破坏模式包括刚性滑块的平动、转动以及平动转动相组合的方式。在实际应用中,平动破坏模式是最常用的。
隧道的变形模式考虑实际工程隧道塌陷事故中,隧道上部以及开挖面前方土体向隧道内部塌陷的实际情况,以及参考 Davis等[9]对隧道变形模式的简化,构造刚体平动破坏模式,如图2所示。破坏模式的速度场由m个刚性块体组成,块体之间由厚度为0的速度间断面相连接,通过2m-1个角度变量确定滑动土体的形态。
为了得到较为精确的支护压力上限解答,同时也为了研究极限分析多块体方法在隧道开挖面稳定中的应用,进一步改进破坏模式,本文通过增加刚性多块体个数(角度变量成倍数增加)进行分析计算,并逐步将计算结果进行分析比较;从而既能更为精确地模拟实际开挖状态,同时又不使计算过于繁琐。
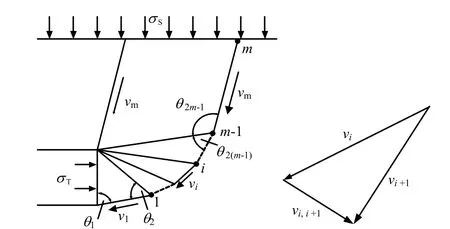
图2 破坏模式及相容速度场Fig.2 Collapse mechanism and the corresponding velocity field
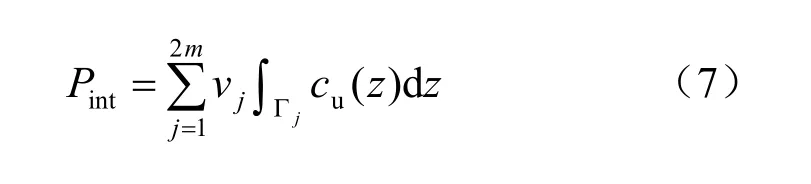
式中:νj和Γj分别表示间速度断面 j的相对速度矢量和面积;
由 Pext=Pint得到:
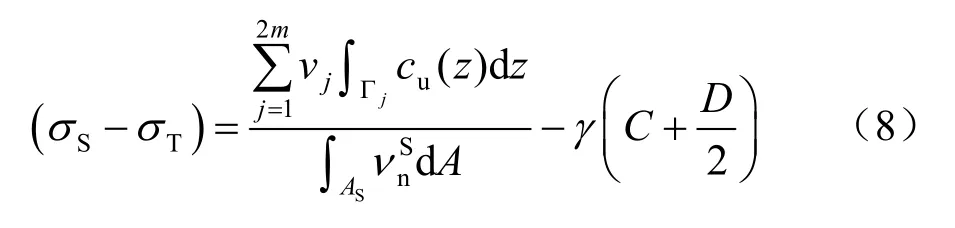
3 隧道开挖面稳定上限分析
根据塑性极限分析上限法[2],在运动许可的速度场内,由外部荷载所做的功等于内部能量损耗得到的荷载即为上限解。
(1)外荷载所作的功
在多块体极限分析上限法中,外荷载和变形土体重力所做的功为

对于理想塑性材料,服从塑性相关流动法则,在不排水条件下,土体积变形前后不发生变化,即:
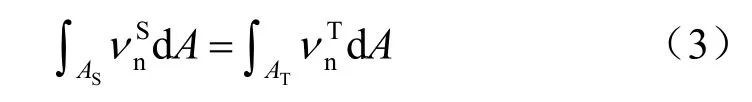
所以有:

(2)速度间断面能量损耗
当破坏模式确定以后,各个速度间断面的速度矢量也就确定了,刚性体滑动相容速度场如图2所示。根据刚性滑块应满足运动许可条件,速度矢量应满足闭合条件的准则[2],则沿速度间断面的速度矢量为
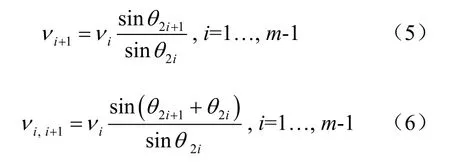
式中:vi+1为第i+1个滑块的速度;vi,i+1为滑块i和i+1的相对速度。
速度间断面能量耗损为
将速度矢量代入式(8),并为方便分析将其无量纲简化得到:
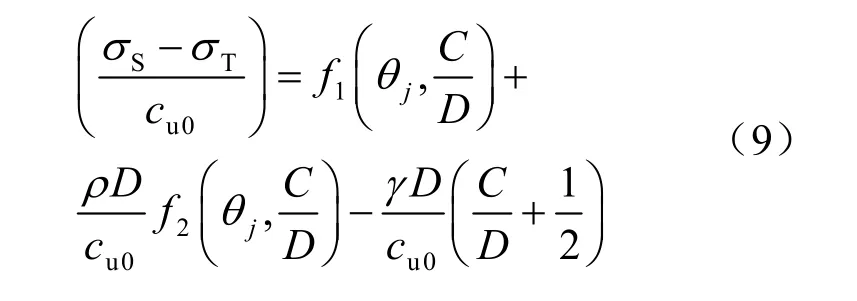
式中: f1是由地表处不排水强度(cu0)引起的能量耗损得到的参数; f2为 0~(C+D)深度范围内不排水强度增量引起的能量损耗得到的系数,是C/D 2次函数。
本文所要解决的问题是:在其他参数(C/D、(ρ D )/cu0、(γ D )/cu0)给定的条件下,至少需要多大的支护压力σT才能保持隧道开挖面稳定避免隧道塌方。结合极限分析上限定理,满足运动许可条件的最大的σT是对应破坏模式的一个最优解。于是问题转化为在满足物理意义约束(相容速度场)、相应参数给定的条件下,寻求荷载参数(σS-σT)/cu0的最小值。
于是根据破坏模式的相容速度约束,确定角度变量的变化范围,通过Matlab软件编程对目标函数式(9)进行优化,可以得到(σS-σT)/cu0的最小上限解,并记录求得最小上限解时对应的角度变量的值。
4 计算结果讨论与分析
4.1 破坏模式的确定
为了得到更为精确的上限解,本文逐步考察了图2所示3个角度变量、5个角度变量、9个角度变量共 17个角度变量的破坏模式下,载荷参数(σS-σT)/cu0的上限解答。任取一组参数(γD)/cu0=3,(ρ D )/cu0=0时,载荷参数随隧道埋深比C/D变化曲线如图3。
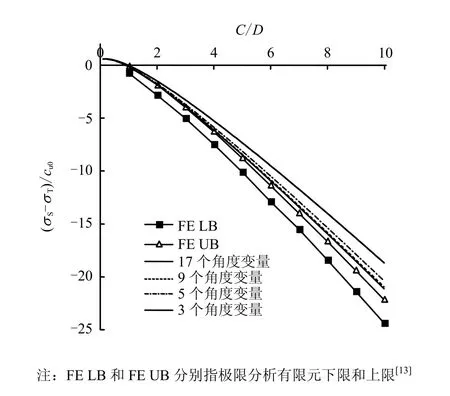
图3 不同角度变量情况下载荷参数上限值比较Fig 3 Comparison of upper bounds for load parameter of tunnel face with constant shear strength for (γ D)/cu0 =3
在平面应变隧道开挖的破坏模式(图 2)中,角度变量越多,计算过程就越复杂,但相应地得到的上限解也得到一定的改善。由图3中可以看到,9个角度变量的破坏模式明显改善了5个角度变量和3个角度变量的上限结果,逐渐逼近Augarde等[13]极限分析有限元的计算结果;但继续增加到17个角度时,载荷参数的上限值改进微小。也就是说就多块体极限分析上限法而言,9个角度变量的破坏模式已经得到足够精确的上限解,可以很好的界定开挖面支护压力准确解的范围。所以下面将以9个变量的破坏模式得到的结果为基础进行分析。
4.2 隧道开挖面稳定性影响因素分析
由上述极限分析上限法以及计算公式(9)可知,软土地区非均质地基中隧道开挖面稳定极限分析上限法能够反映隧道埋深、土体重度、以及土体强度(随深度变化)等对隧道开挖支护压力的影响。
图4为土体重度一定、不排水强度随深度呈线性变化时,载荷参数随隧道埋深比的变化曲线。不难发现,对于均质土((ρ D )/cu0= 0),若不考虑土体重度(图4(a)),则隧道埋深越大,保持开挖面稳定所需的极限支护压力越小;若考虑土体重度(γ D )/cu0(图4(b)),则隧道埋深越大,保持隧道开挖面稳定所需的极限支护压力也越大(载荷参数越小)。当地基土不排水强度随深度线性增加时((ρ D )/cu0>0),则随着隧道上覆土层厚度的增大,保持隧道开挖面稳定所需的极限支护压力逐渐减小(但其趋势并不是完全一致,在下面另有讨论),这是由于土体发挥抗剪强度的效果。
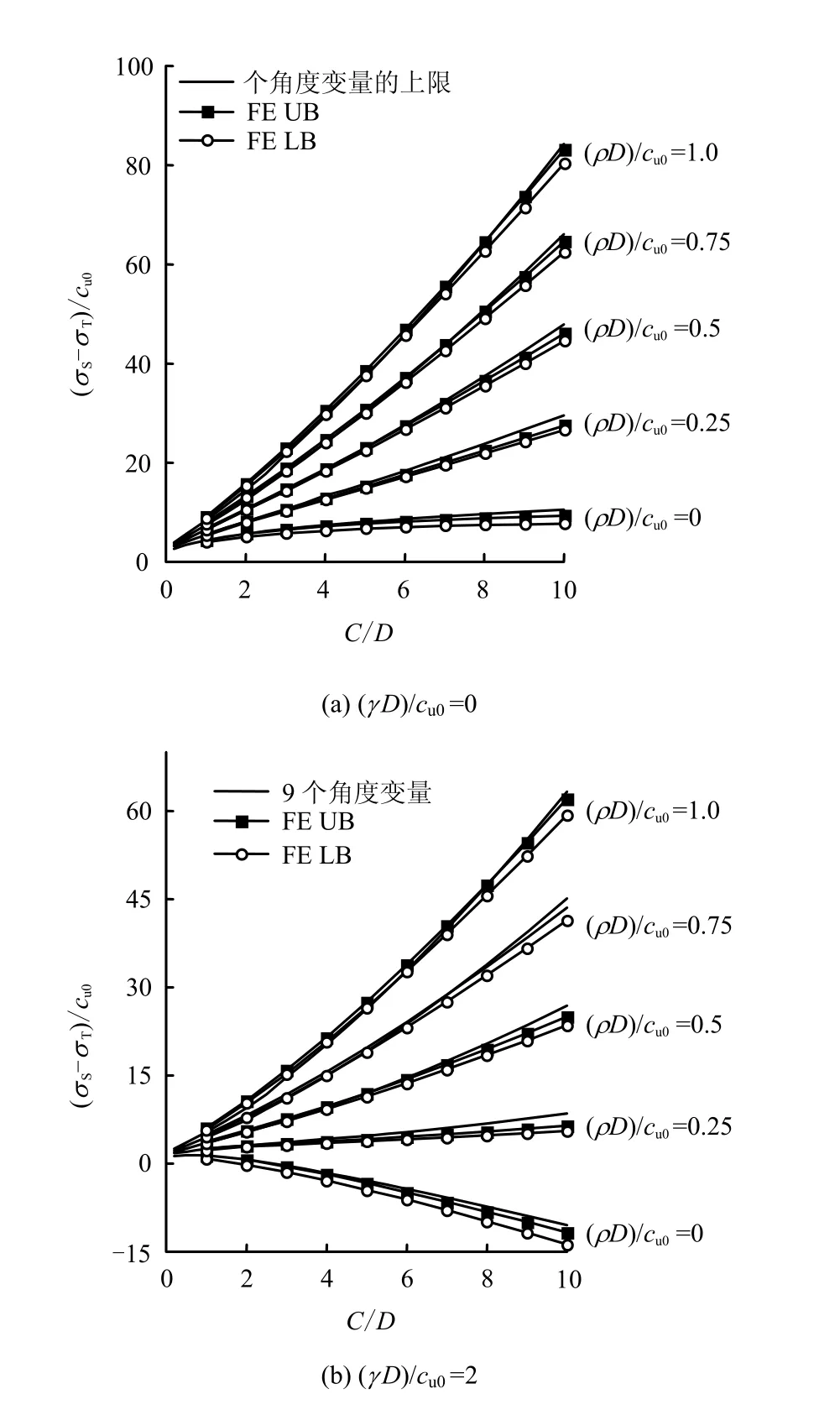
图4 荷载参数受非均质影响的对比曲线Fig.4 Upper bounds on load parameter for different (ρ D)/cu0
而且随着非均质参数(ρ D )/cu0的逐渐增加,由极限分析上限法得到的载荷参数(σS-σT)/cu0越来越逼近(埋深比小时甚至小于)Augarde等[13]等由极限分析有限元得到的上限值。这充分说明了本文多块体极限分析上限法对于非均质地基隧道开挖面稳定性分析的可行性。尤其是当隧道埋深较小时(C/D<6),极限分析上限法可以得到足够精确的上限解,将准确解界定在足够小的范围之内。
隧道开挖面稳定荷载参数与土体重度呈反比例线性关系(式(9)),土体重度越大,保持盾构隧道开挖面稳定所需支护压力就越大(荷载参数逐渐减小),如图5所示。当隧道埋深一定时,不管不排水强度是否随深度变化,曲线斜率一定;而且隧道埋深比越大,曲线斜率越大(在式(9)中亦可看出)。

图5 载荷参数在不同隧道埋深时随容重变化曲线Fig.5 Load parameters replotted for varying weight parameter
需要注意的是,从图5、6的对比分析中可以明显看到,隧道埋深对载荷参数的影响并不是一成不变的,其间要考虑到土体重度和土体强度的作用。在图5载荷参数随重度的变化曲线中可以看到,当非均质参数一定时,存在一重度临界点当时,埋深越大,保持隧道开挖面稳定所需的支护压力越小(载荷参数越大);当时,埋深越大,则保持隧道开挖面稳定所需的支护压力越大(对比图4载荷曲线随深度的变化曲线的趋势亦有此现象)。而且这是由于土体不排水强度和重度耦合作用的结果。在上述极限分析上限解式(9)中,土体强度与载荷参数呈正比例非线性关系,而重度与载荷参数呈反比例线性关系,所以当重度相对较小时土体强度对荷载参数的影响占主导地位;而当土体重度较大时土体容重对荷载参数的影响占据主导地位。在图5(a)~(e)随着非均质参数(ρ D )/cu0的增大,临界点也越大,即土体强度占主导地位的重度范围越大。
同样地机制,当土体重度一定时(见图6),非均质参数亦存在一临界点当时,埋深越大,保持隧道开挖面稳定所需支护压力则越大(土体重度的影响占主导地位);当时,埋深越大,所需支护压力则越小(土体强度的影响占主导地位)。
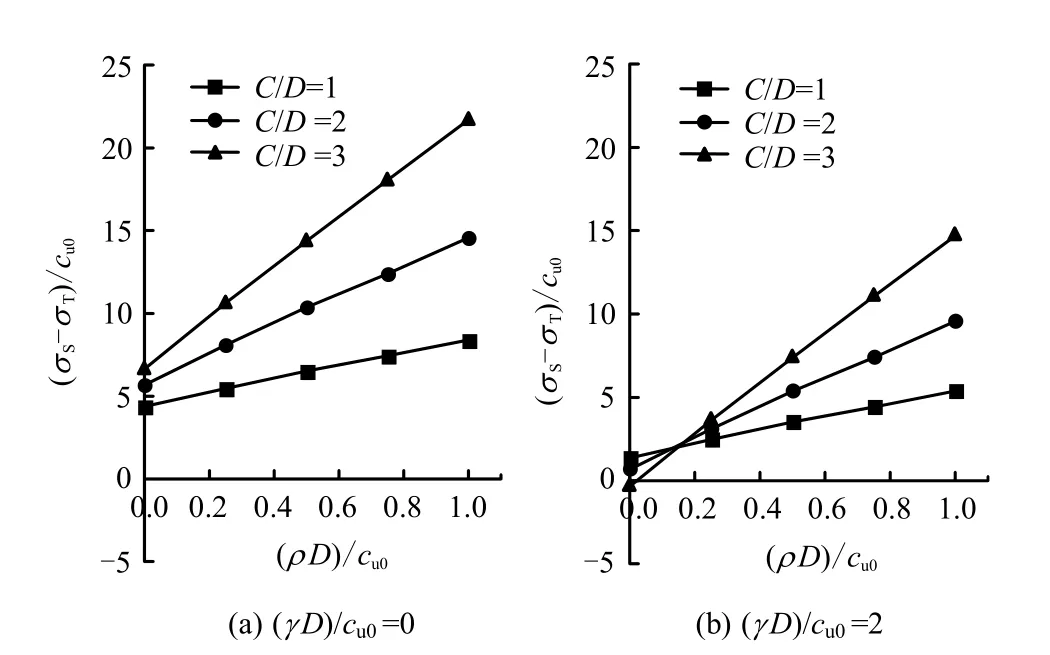
图6 荷载参数随非均质参数的变化Fig.6 Load parameters replotted for varying nonhomogeneous parameter
总之,在实际工程设计中,当根据隧道的埋深确定盾构开挖面支护压力时,必须同时考虑土体的重度和土体强度随深度变化的影响,以及二者的耦合作用,否则得到的支护压力偏小或者是偏大时,容易引起地基沉降变形过大,甚至于出现塌陷,或者有可能造成地表隆起,对周围环境的影响也是十分不利的。
4.3 开挖破坏面
由多块体极限分析上限法,得到优化后的某一埋深时软土地层隧道开挖面失稳后纵断面破坏如图7所示。

图7 优化后的破坏模式(当埋深一定时)Fig.7 Collapse mechanisms by optimization for different depths of plane strain heading tunnel
与隧道开挖面稳定极限支护压力不同的是,优化后的破坏模式不受土体重度的影响,无论土体重度如何变化,在隧道埋深及土体强度一定的情况下,隧道开挖面破坏时前方和上方的土体滑动变形范围及破坏面形式是一致的。
但土体强度变化参数对破坏模式有显著的影响:首先,考虑土体的非均质性后,开挖面失稳破坏引起的上前方土体滑动影响范围变小,而且随着土体强度变化参数(ρ D )/cu0的增大,其影响范围愈小(C/D =0时,开挖面前方土体滑动范围为0.25~0.5D((ρ D )/cu0从0到1);C/D =1时,开挖面前方土体滑动范围为1.4~1.7D;C/D =3时,开挖面前方土体滑动范围为1.9~2.7D);开挖面前方滑动土体倾角呈减小趋势,但变化不大。其次,从图 7(b)、和图7(c)的对比中可以看到,随着土体非均质系数的增大,开挖面上前方土体越来越趋于整体破坏(多个刚性滑块体逐渐重合)。而隧道埋深越大,则隧道开挖面上前方滑动土体的范围就越大。
5 结 论
本文针对平面应变隧道,基于极限分析上限法的刚性多块体平动破坏模式,考虑隧道埋深、土体重度以及不排水抗剪强度随深度变化率的影响,推导了隧道开挖面稳定支护压力的上限公式;得到极限支护压力的最小上限解;通过与现有计算结果的对比和参数分析可以得到以下结论:
(1)极限分析有限元结果的对比表明,多块体极限分析上限法可以得到足够精确的上限解,验证了解答的有效性,为简单有效地确定浅埋隧道开挖极限支护压力提供了一个可行的方法,具有一定的实践指导意义。
(2)参数分析指出:隧道开挖面稳定极限支护压力随土体重度的增加而线性增加,随非均质参数的增加而线性减小,埋深对极限支护压力的影响则取决于土体重度和强度的共同作用。在实际工程设计中若忽略土体重度则得到的支护压力偏小,若不考虑强度非均质则得到的支护压力偏大,对于隧道稳定设计都是不利的。
(3)隧道失稳后纵断面破坏模式与土体重度无关;而考虑土体强度非均质性后,开挖面失稳引起的上前方土体滑动范围变小,且随着非均质参数的增加,其影响范围愈小。
[1]尹旅超, 朱振宏, 李玉珍译. 日本隧道盾构新技术[M].武汉: 华中理工大学出版社, 1999.
[2]CHEN W F. Limit analysis and soil mechanics [M]. New York: Elsevier Scientific Publishing Company, 1975.
[3]MAIR R J. Centrifugal modelling of tunnel construction in soft clay[D]. Cambridge: University of Cambridge, 1979.
[4]VERMEER P A, RUSE N, MARCHER T. Tunnel heading stability in drained ground[J]. Felsbau, 2002,20(8): 8-18.
[5]LI Y. Stability analysis of large slurry shield-driven tunnel in soft clay[J]. Tunnelling and Underground Space Technology, 2009, 24(4): 472-481.
[6]EISENSTEIN Z, SAMARASEKARA L. Stability of unsupported tunnels in clay[J]. Canadian Geotechnical Journal, 1992, 29: 609-13.
[7]ANAGNOSTOU G, KOVARI K. Face stability conditions with earth-pressure-balanced shields[J]. Tunnelling and Underground Space Technology, 1996, 11: 165-73.
[8]ATKINSON J H, POTTS D M. Stability of shallow tunnel in cohesionless soil[J]. Geotechnique, 1977, 27(2): 203-215.
[9]DAVIS E H, GUNN M J, MAIR R J, et al. The stability of shallow tunnels and underground openings in cohesive materials[J]. Geotechnique, 1980, 30(4): 397-416.
[10]LECA E, DORMIEUX L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material[J]. Geotechnique, 1990, 40(4): 581-606.
[11]SLOAN S W, ASSADI A. Undrained stability of a plane strain heading[J]. Canadian Geotechnical Journal, 1994,31: 443-500.
[12]SLOAN SW, ASSADI A. Undrained stability of a square tunnel whose strength increases linearly with depth[J].Computers and Geotechnics, 1991, 12: 321-46.
[13]AUGARDE C E, LYAMIN A V, SLOAN S W. Stability of undrained plane strain heading revisited[J]. Computers and Geotechnics, 2003, 30: 419-430.

