经济学与肥料学中报酬递减律的同一性及其问题

褚清河，强彦珍

（1.山西省农业科学院农业资源与经济研究所，山西太原030006；2.太原高新技术产业开发区园林绿化管理中心，山西太原030006）

肥料报酬递减律是施肥学上的一个重要理论，它是确定施肥量与产量函数关系的基本理论，即确定最高和最佳产量施肥量的理论依据。报酬递减理论的提出并非植根于肥料研究，而是移植于经济学[1]。由于经济学报酬递减律研究的是投入与产出的数量关系，而投入这一复合因素中无一例外地包括了肥料投入，显然二者必然具有同一性。事实上，由于施肥量和产量是经济学上投入与产出的具体内容，且具有一一对应的函数关系，经济学报酬递减律理应基于二者进行深入试验和分析，可是经济学报酬递减律是在没有严格划分投入产出的自变量和因变量及确立其函数关系的情况下的一种推论，其中的错误或不足也就在所难免，因此，讨论经济学与肥料学中报酬递减律异同及其存在的问题，仍具有十分重要的意义。

1 经济学报酬递减律及其问题

1.1 报酬递减律的定义

早在18世纪后期，欧洲的经济学家就根据投入与产出的关系，提出了报酬递减律，成为经济学的一个定律或法则。报酬递减律一般定义：从一定土地所得到的报酬，随着向该土地投入的劳动和资金数量的增大而增加，但随着投入的单位劳动和资金的增加而逐渐减少。几百年来，这一理论广泛应用于工业、农业以及牧业生产等各个方面，几乎没有一个重要的经济学家不曾谈到它，这一理论研究的先驱就是欧洲经济学家杜尔哥和安德森。虽然至今，其在国内经济理论界仍然存在争议，但多数学者还是具有一致的观点，即报酬递减规律是在其他条件不变的情况下得出的结论。边际报酬递减规律存在的原因是：随着可变要素投入量的增加，可变要素投入量与固定要素投入量之间的比例在发生变化；在可变要素投入量增加的最初阶段，相对于固定要素来说，可变要素投入过少，因此，随着可变要素投入量的增加，其边际产量递增，当可变要素与固定要素的配合比例恰当时，边际产量达到最大；如果再继续增加可变要素投入量，由于其他要素的数量是固定的，可变要素就相对过多，于是边际产量就必然递减。如果要素比例是固定的，这个规律就不成立。在这里，如果要素均为可变要素且与产出具有一一对应的函数关系[2]，这种认识无疑是正确的。但是，在投入的要素中并非均为可变因素，也非均具有一一对应的函数关系。如劳动或资金是经济学中所说的生产要素，但劳动和资金显然不是直接影响产量的自变量。

由此可见，杜尔哥和安德森提出的报酬递减律是不存在的，或者说是不正确的。首先劳动和资金并非土地所获报酬（产品或产值）的直接变量，即可变要素，不存在相应的函数关系，自然也就不存在报酬递减规律。假如报酬递减律中的劳动和资金代表的均是可变要素，由于不同的要素对土地产出的产品或产量的贡献大小不同，由此，在进行生产投入时各要素之间必然要保持一个最佳比例，才能获得最大的经济效果，这样在地力、品种以及自然条件所允许的可变要素最大投入量之前，可变要素的边际报酬应该是常数，把可变要素固定为常量必然会得出报酬递减的结论。

1.2 经济学报酬的含义与劳动、资金的属性

很早以前，我国劳动人民开始辟地种植作物，连种几年后，土壤肥力消耗，产量减退，就实行撂荒，另辟新地。到商周创立井田制，才开始抛荒轮休，以恢复地力，之后以青草肥田。西方国家对于植物营养的研究始于文艺复兴之后。在19世纪之前，人们甚至还认为，作物的生长是由于作物种子和土壤里潜伏着一种神奇的力量，作物借着它而获得产量。因此，在人们对植物营养与产量的关系还一无所知的情况下，不可能深入研究投入和产出的经济关系，也只能从劳动和资金的投入对产量的影响中，探索一定土地上劳动和资金的合理投入量。但在对影响作物产量增减要素十分明了的今天，必须用现代的科学研究结果，重新认识杜尔哥报酬的涵义、劳动和资金的属性及其与报酬的关系。

杜尔哥的报酬递减律思想主要体现在对德·圣·佩哈维先生文章的评论中。佩哈维先生对若干个土地肥沃、大面积耕作的农场所作的投资和它们的产量进行了统计，得出的计算结果是每年的投资与总产量之间的比例为2∶5，由此得出结论说，耕作者的收入不能受到侵犯，如果税收使耕作者减少投资，那么产量就要和投资成等比例减少。杜尔哥认为，我们无权从这个特殊的计算中得出一个带有普遍性的结论，在投资和产量之间不可能有一种固定不变的比例。从佩哈维先生的论述和杜尔哥的评论中可以看出，他们讨论的是大面积耕作农场的投资和产量，而非在农场从事建筑及其他产业。由此可以认为，经济学中所讲的报酬就是指耕作土地上农作物的产量。杜尔哥报酬递减律的思想集中体现在如下事例中。

撒在一块天然肥沃的土地上的种子，如果没作任何土地的准备工作，这将是一种几乎完全损失的投资。如果只添加1个劳动力，产品产量就会很高；第2个，第3个劳动力不是简单地使产品产量增加1倍或2倍，而是增加3倍或9倍，这样，产品产量增加的比例会大于投资增加的比例，直到产量增加与投资增加的比例达到它所能达到的最大值为止。超过这一点，如果我们继续增加投资，产品产量也会增加，但增加得较少，而且是越来越少，直到土地的肥力被耗尽、耕作技术不会再使土地肥力提高时，投资的增加就不会使产品产量有任何提高了。在这里，杜尔哥讨论了生产要素资金投入对产量的影响及其产出变化的过程。在这一例子中，资金的投入首先包括了种子，但种子的投资如不借助于劳动就谈不上提高产量，必然导致完全损失用于种子的投资。在杜尔哥看来，劳动本身不仅是农业生产中的重要投资，而且农业生产中更多资金的投入，如耕作、除草、施肥、灌水、喷洒农药等，都需通过劳动才能起到增产作用。因为，撒一粒种子在肥沃的土地上并添加一定的劳动力可增加几倍的产量。这清楚地表明，经济学中的生产要素，如资金和劳动中许多生产要素，并不完全是作物产量的自变量，大多数生产要素，如耕作、除草、喷洒农药、平田整地、作物品种更新等，均为适量变量或者说阶梯变量，即到达适量水平后产量提高一个台阶，但在未达到一定程度或达到适量后再增大这一要素，则不具有增产效果。因此，投资和劳动必须借助于影响产量增减变化的可变因素如施肥量，才能起作用，因为施肥量和作物产量具有一一对应的函数关系。

1.3 经济学报酬递减的实质

1.2 讨论表明，杜尔哥报酬递减律中的报酬指的是农作物的产量，而资金是一种复合生产要素，资金的投入也可表现为劳动，但多数生产要素是适量变量或阶梯变量，它们与产量并不具有一一对应的函数关系，因此，在杜尔哥产量增加与投资增加的比例达到它所能达到的最大值之前，也就不可能出现报酬递减的问题。

无论社会科学研究还是经济学研究，均属于宏观战略研究的范畴，它们都是建立在基础科学研究之上的。杜尔哥之所以得出报酬递减的结论，是因为杜尔哥本人及其他经济学家没有也不可能将资金和劳动中各个生产要素一一进行分离，并与产量进行显著相关性试验研究之故。例如，劳动既是资金的投入形式，也是资金提高作物产量的载体，而劳动在农业生产中表现为中耕除草、平整土地或耕作时，不仅对除草干净程度与保持无草的时间、耕作次数和平整土地的水平程度与产量的关系无法定量，而且如坡地平整具有增产作用，也并非平整一次就增产一次、地越平整越增产，通常只有培肥后才具有增产效果。同样，中耕具有增产效果，但也并非中耕次数越多越增产，锄草越干净越增产。在这些作业上的投资或劳动究竟达到什么程度就增产，什么程度就不增产，是无法准确度量的。因此，也就无法确定每项作业的投工数或资金，必然是有的投工可能过多，而有的偏少。其次，投工过多时，多投的工不具有增产效果，会造成资金浪费，过少时不能显现出增产作用。当然也由于不可能同时在一定的土地上增加投资改善所有产量要素，只能是先改善最重要的产量因素，通常农业经营在一开始投资少的时候，必然是首先改善与产量密切相关的因素，如播种施肥、中耕锄草、灌溉等，花费在这些作业上的投资或投工量也基本在合理的程度内，此时，单位劳动必然获得较高的报酬，但随着一定土地投资的增加，用于播种施肥、中耕锄草、灌溉等的用工就有可能过量，而着眼于长远效益改善农田基本条件的工作也将逐步实施，这些劳动很可能多年不能得到回报，综合投资的单位报酬就会出现递减状况，显然这不是投资和产量的自身规律，而是资金投向某一生产要素的量、时间或流向与现实产量目标不一致造成的，并非自然规律。

2 肥料报酬递减律是经济学的重要研究内容

2.1 传统研究方法下施肥量与作物产量的函数关系

施肥学研究表明，在耕作、播种、中耕除草、灌溉、施肥等生产要素中，施肥是直接影响作物产量提高的可变因素，也是经济学中的重要投入要素，经济学报酬递减律理应通过研究二者的函数关系而获得。但由于作物营养与施肥理论研究的滞后，直到19世纪才有可能。经济学报酬递减律提出后，到19世纪，作物营养学研究才取得很大进展，作物营养研究结果表明，决定作物产量增加的是土壤中作物生长必需的营养元素。随着李比希最小因子理论的提出，施肥量与产量函数关系的研究已成为19世纪早期施肥科学的重大课题。米采利希（Mitscherlich）在前人工作的基础上，深入探讨了施肥量与产量的关系，从而发现，随着施肥剂量的增加，所获得的增产量具有递减的趋势，据此认为，与经济学上的报酬递减律相吻合，确切地说，是经济学报酬递减律研究的科学的开端。米采利希后，斯皮尔曼（Spillman）总结了棉花施用完全肥料的报酬递减情况并以数学式表达为y=A（1-Rx）。20世纪80年代，张大弟在施用有机肥的基础上进行的施氮用量试验也表明，边际产量同样呈递减规律。基于这一规律，人们普遍认为，作物施肥量和产量的函数关系可用一元二次回归方程来表征，应用一元二次回归方程求解作物最大施肥量就成为国内外至今普遍应用的传统方法[3]，肥料报酬递减律也成为施肥学上的经典理论。人们一般认为，该理论是移植于经济学或借鉴了经济学报酬递减律的思想。科学地讲，肥料报酬递减律应是较经济学报酬递减律更科学的深入研究。因为肥料学报酬递减律研究把肥料及其施用量这一可变因素从资金或劳动中有效分离出来，进而研究施肥量变化对产量的影响及二者的函数关系，不能不说是物理定性和数学定量研究的有机结合。

然而，米采利希及其后人在研究施肥量与产量的函数关系的试验中存在明显不足。米采利希在盆栽试验中，把试验的养分分作许多剂量供给，相邻剂量保持一定差量，其他养分保持充分供给，环境条件保持均一。试验结果表明，在其他技术条件相对不变的前提下，随着施肥剂量的渐次增加，产量也随之增加，但把累积增产量画在以施肥量为横坐标的图上，得到的结果不呈瓦格诺尔和麦耶所设想的直线上升，而是呈一对数曲线，据此得出肥料报酬递减的结论，提出了著名的肥料报酬递减理论。乌尔尼教授认为，限制因子施用超过最适量时就变成毒害因素，使产量降低，因此费佛尔（Pfeiffer）教授等提出了抛物线图式，并受到普遍认可。但不管是米采利希试验养分保持一定差量，其他养分充分供给的试验方法，还是斯皮尔曼的完全肥料试验均有悖于最小因子理论或不遵从单一差异原则。物理学能量守恒定律表明，能量既不会凭空产生，也不会凭空消灭，它只能从一种形式转化为其他形式，或者从一个物质转移到另一个物质。作物每形成100 kg经济产量所需的氮磷钾元素基本上应该是一常量，因此，在作物最高产量施肥量范围内，单位剂量肥料的增产量也就应该是常数，之所以出现肥料报酬递减现象，是由于该养分的吸收转化率降低，而降低的原因就是在最大施肥量范围内，其他养分不能成比例地有效供给之故。由此可见，肥料报酬递减律不符合能量守恒定律。

2.2 氮磷等比试验条件下施肥量与产量的函数关系

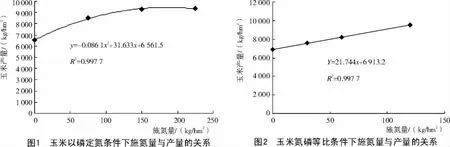
事实上，米采利希学说在当时就受到一些学者的质疑，他们认为，米采利希试验是在各种条件不变，只有一个养分施用的数量不同成为变量时取得的结果，这里可能出现第2个或第3个限制因子。如果把它们同时改变就可能取得直线上升的结果，这与目前认为经济学边际报酬递减规律存在的原因分析结论是一致的。本试验研究表明，玉米以磷定氮试验条件下，在玉米最高产量施肥量范围内，施氮量与产量的函数图形为抛物线。

从图1可以看出，施氮量在大于75 kg/hm2后，不同施氮量的玉米产量无显著差异，施氮量在225 kg/hm2的范围内，玉米边际产量呈递减规律，但施氮量与施磷量保持1∶1的最佳施肥比例下增加施肥量，施肥量与玉米产量的函数关系为直线图形（图2），此时玉米边际产量为常数，并非呈递减规律，这表明，过去学者们对米采利希的质疑是正确的。米采利希在试验中把试验因子以外的其他变量固定为一常数，实际就是把影响产量变化的变量作为常量来看待，用一个氮元素来表征由氮磷甚至是氮磷钾大量元素的共同作用，因此，当施氮量逐渐增大的同时，氮磷比例却逐渐变小，必然导致单位肥料的玉米增产量降低。

从表1可进一步看出，氮磷等比试验方法下，施氮量小于120 kg/hm2时，每千克氮肥平均增加玉米产量10.8 kg，边际产量变化较小，基本上为一常数；施氮量大于120 kg/hm2时，玉米的边际产量则显著降低；施氮量为240 kg/hm2的处理仅为2.7 kg。这里以相交直线计算的玉米最高产量施氮量为126 kg/hm2，它与玉米边际产量显著降低时的施氮量一致，说明最大施氮量是边际产量由大变小的转折点，以相交直线计算的最大施氮量较一元二次回归方程更能表征这种变化规律[3-5]。

表1 2004年玉米氮磷等比与以磷定氮条件下的边际产量 kg/hm2

在施用120 kg/hm2磷肥而改变氮肥用量的试验方法下，玉米边际产量如按第1个施氮处理减去单施磷对照产量再除以施氮量的传统方法计算，玉米边际产量呈递减规律，但这种计算方法没有考虑氮、磷配合施用的效应远大于氮、磷单施效应之和的问题，它与施氮处理间相减不具有同一性质。这种计算使得施氮量为75 kg/hm2的边际产量高达26.5 kg/hm2，但它与空白对照相减再除以氮、磷总用量，则为每增加1 kg氮肥玉米增产8.3 kg，这时玉米边际产量随施氮量的增加而增加，到接近以相交直线计算的最大施氮量141 kg/hm2的处理，玉米边际产量达到10.3 kg。施氮量大于141 kg/hm2时，玉米的边际产量显著降低，施氮量为225 kg/hm2的边际产量仅为0.6 kg，这与氮磷等比试验方法下的结果具有一致的变化规律。可见，肥料报酬递减律是施肥理论和施肥试验方法不完善与计算失误下得出的一种结论，并非科学规律[6-7]。

3 结论与讨论

经济学报酬递减律研究的是生产要素劳动和资金与作物产量投入与产出的关系。在这里，劳动和资金是一种复合生产要素，它们对作物产量的作用必须借助于一些适量常量如种子、农药、播种、平整土地；阶梯变量如中耕除草、灌溉；直接变量如肥料等载体才能产生影响，并非直接影响作物产量的增减。在劳动和资金的这些载体中，只有肥料施用量与作物产量才具有一一对应的函数关系。因此，在农业生产中研究投入产出报酬问题的科学出发点就应着眼于肥料投入与产出的数量关系。因为生产要素与作物产量如果不具有一一对应的函数关系，也就不存在随着劳动和资金投入的增加报酬递减的问题。杜尔哥之所以得出报酬递减的片面结论，是因为杜尔哥本人及其他经济学家没有也不可能将资金和劳动中各个生产要素一一进行分离，并与产量进行显著相关性试验研究之故。因为在杜尔哥时代，人们对作物营养的问题还一无所知，自然不可能对投入产出关系进行深入科学研究。施肥科学的发展为施肥量与作物产量投入产出报酬问题的科学研究提供了可能。然而，在氮磷最佳施肥比例的概念还没有提出之前，不可避免地要犯米采利希把试验因子以外的其他变量固定为一常数的错误。固定试验因素以外的因子为相同水平，实际就是把影响产量变化的变量作为常量来看待。在氮磷肥料试验中固定磷为同一施肥量水平，当施氮量逐渐增大的同时，氮磷比例必然逐渐变小，从而导致单位肥料的玉米增产量降低，得出肥料报酬递减的片面结论。经济学报酬递减律和肥料报酬递减律实为同一内容的同一命题，肥料投入应是经济学研究报酬问题的唯一内容。研究表明，在最佳氮磷比例条件下和最大施肥量范围内，作物的边际产量基本为一常数，并非呈现递减规律。

［1］谭金芳.作物施肥原理与技术[M].北京：中国农业大学出版社，2009：19-21.

［2］中国经济50人论坛.马克思主义与报酬递减律[EB/OL].[2004-10-28].http://www.cei.gov.cn/doc/50ren/XuShanDa/txt 01.htm.

［3］褚清河，潘根兴，李典有，等.氮磷等比与以磷定氮条件下玉米的最大施肥量研究[J].土壤学报，2007，44（6）：1083-1089.

［4］褚清河，潘根兴，王成己.玉米产量与施氮量的依变规律及实质研究[J].土壤通报，2009，40（6）：1356-1361.

［5］姜孟祥，张拴庄，薛世川，等.肥料合理调配对土壤养分动态及小麦产量的影响 [J].华北农学报，2008，23（增刊）：286-289.

［6］褚清河，强彦珍.也谈中国主要粮食作物生产中肥料利用率及其提高途径[J].山西农业科学，2010，38（9）：3-8.

［7］褚清河.玉米氮磷最佳施肥比例与报酬递减律研究[J].山西农业科学，2009，37（11）：23-25.