旋转机械振动状态监测中的不平衡量相位提取方法
林可
(中煤科工集团重庆研究院 重庆 400037)
在旋转机械监测与故障诊断中,振动监测是主要的手段之一,利用振动信号对故障进行监测与诊断是设备故障诊断方法中最有效、最常用的方法。振动是旋转机械产生故障的主要原因,转子不平衡又是产生振动的主要原因。
在动平衡测试系统中,经常要对转子振动的周期信号作频谱分析,常规方法是求频谱采用快速傅里叶变换(FFT),其计算量小,速度快。周期信号的频谱是离散的,只有整周期采样才能准确地获得周期信号的幅值和相位,因此无论被测信号的转子转速如何变化,在转子一个转速周期必须采样相同的点数。
1 采样频率和误差的关系
精确地获取不平衡量的幅值和相位是进行转子动平衡的前提。
在信号的采样中,若拟定最大丢失0.2%;设信号的某次频率为f,幅值为A;设波形幅值在α处下降至0.998 A。按在采样中最大0.2%的幅值漏掉的要求,有可得出 α<3.624°,如表 1所示。

可见当采样频率为信号频率的100倍以上时,才不致把信号最大幅值的0.2%丢失,即采样频率为fc=100 f。综合考虑采样精度和采样数据容量的因素,本设计系统中将转速信号128倍频。周期信号的频谱是离散的,只有整周期采样才能准确获得周期信号的幅值和相位。
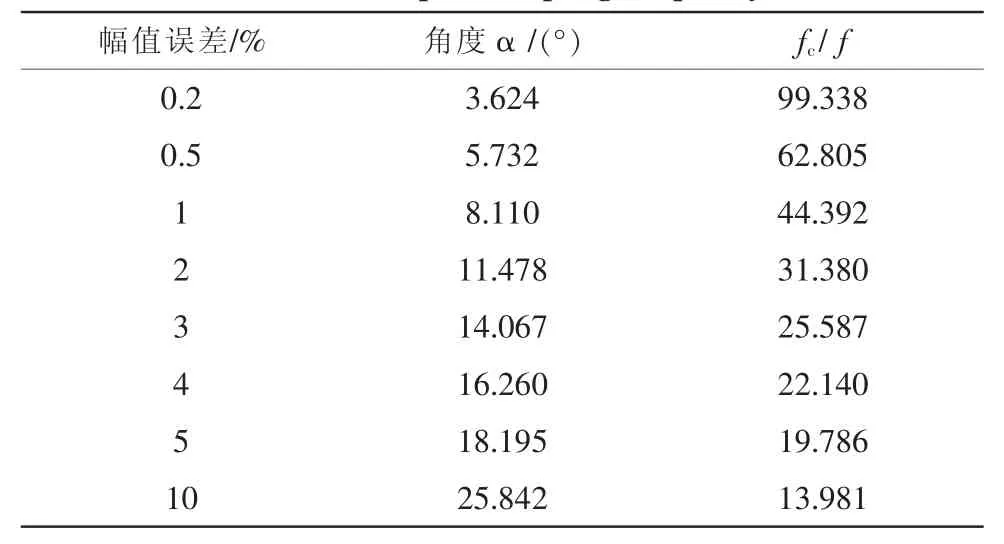
表1 采样频率和误差关系Tab.1 The relationship of sampling frequency and error
2 锁相环实现整周期采样
2.1 锁相环的工作原理[1-2]
在通常周期采样中采用定时采样的办法,即将转子标记起始刻度,用光反射方法或霍尔原理记时转子一个转动周期而采样。由于采样频率固定,随转速不同,采样点数不确定。当高频时可能采样点数不够,而低频时又会采样过多的数据而影响计算速度。因此定时采样的方法不能满足系统对一个周期必须采样相同的点数要求。
锁相的意义是相位同步的自动控制,能够完成两个电信号相位同步的自动控制闭环系统叫做锁相环,简称PLL。在现代电子技术中,为了得到高精度的振荡频率,通常采用石英晶体振荡器。但石英晶体振荡器的频率不容易改变,利用锁相环、倍频、分频等频率合成技术,可以获得多频率、高稳定的振荡信号输出。输出信号频率比晶振信号频率大的称为锁相倍频器电路;输出信号频率比晶振信号频率小的称为锁相分频器电路。
所谓锁相,就是实现相位同步。能使两个电信号的相位保持同步的闭环系统叫锁相环。锁相环主要包括3部分:鉴相器、低通虑波器、压控振荡器(VOC)。其结构框图如图1所示。

图1 锁相环的结构框图Fig.1 Structure diagram of phaselocked loop
这是一个相位自动跟踪的负反馈系统。鉴相器用来将两个输入信号Ui与Uo之间的相位差转换成误差电压Ue输出作为压控振荡器(VCO)的控制电压。低通滤波器用以滤除鉴相器输出的高次谐波及噪声,压控振荡器作为锁相环电路的脉冲发生器,其振荡频率受控制电压的改变而改变。压控振荡器的输出Uo接至鉴相器的一个输入端,施加于鉴相器另一个输入端的外部输入信号Ui与来自压控振荡器的输出信号Uo相比较,比较结果产生的误差输出电压正比于Ui和Uo两个信号的相位差,经过低通滤波器滤除高频分量并让设定频率的有用信号顺利通过后,得到一个平均值电压Ud。这个平均值电压Ud朝着减小VCO输出频率和输入频率之差的方向变化,直至VCO输出频率和输入信号频率获得一致。这时两个信号的频率相同,两相位差保持恒定同步称作相位锁定。
环路一旦入锁后,输出信号与输入信号的相位相等,也就是输出频率与输入频率获得一致。当锁相环入锁时,它还具有“捕捉”信号的能力,VCO可在某一范围内自动跟踪输入信号的变化,如果输入信号频率在锁相环的捕捉范围内发生变化,锁相环能捕捉到输人信号频率,并强迫VCO锁定在这个频率上。
如果在图1的反馈回路中加入一个N分频器,则可实现倍频功能,如图2所示。根据反馈,Fi=Fo/N即Fo=Fi×N,环路锁定后频率为Fo=Fi×N,实现了输出频率Fo是输入频率Fi的整数倍,只要改变分频器的分频比(1/N)就可以改变锁相环路的输出频率。

图2 锁相倍频结构框图Fig.2 Structure diagram of phaselocking frequency multiplication
2.2 锁相倍频的实现
目前,国内外通用与专用集成锁相环电路已有数百个品种。其中,CD4046A最高工作频率为1.2 MHz[3]。按本系统要求,最高可采样转速9 300转/分的转子。电源电压为5~15 V,是低功耗数字型锁相环。该芯片市场常见,应用成熟。
本系统中应用的锁相环路,锁相用CD4046A,分频器采用CD4024进行128倍分频。将分频器其接在压控振荡器及相位比较器中,作为CD4046A的反馈,则整个电路输出频率为输入信号频率的128倍,整形后的基准脉冲信号Ain经过锁相环128倍频后触发AD采样,以保证整周期同步128个点采样,如图3所示。采用此锁相倍频技术以后,无论转速怎么变化,系统都能保证对有用信号整周期截取,自动调整采样周期。
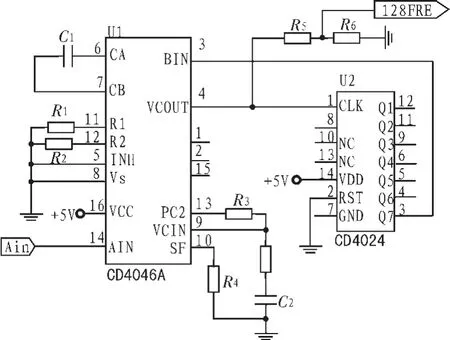
图3 128倍锁相倍频采样环电路原理图Fig.3 Circuit principle diagram of 128 times phaselocked frequency multiplication sampling rings
在实际应用系统中利用DSP芯片TMS320F2812的内部硬件结构、高速的实时数据采集和数字信号处理功能,结合本系统要求的功能与F2812的特点进行分析选择。
3 DFT提取不平衡量振幅和相位[4-6]
转子在高速旋转过程中,通过传感器转换后的反映不平衡振动波形的算式

式中幅值An与不平衡量成正比,φ为不平衡量相位角,平衡时去重机构根据不平衡量大小在相对初始零位φ处进行相应去重,从而使转子动不平衡量减少。然而通过动平衡单、双面平衡影响系数法计算得到不平衡量后,平衡时还必须具体确定增减不平衡量大小的位置。
通常对相位的提取有两种方法:一种是最大振幅求相位法如图4所示,即不平衡相位角φ为不平衡振动信号最大值(振幅)同基准信号上升沿之间所对应相位夹角。该方法的关键在于必须从不平衡周期振动信号中提取一组稳定的不平衡振动信号和基准信号。然而在实际测试中由于现场各种噪声的干扰,尤其是A/D采样本身对模拟信号离散化的固有特点,造成在对振动信号最大幅值提取的偏差或失真。因此针对转子不平衡量相位的提取方法采用基于DFT的不平衡相位提取法更精确。
转子不平衡振动信号为周期振动信号,其特征频率为转子转频,即一倍频,是DFT各次谐波分量中的基波分量。因此采用DFT求不平衡振动信号的相位,就是求解复频域的基波变换。在进行DFT提取基波成份时,可以将其等效为针对基波和各次谐波频率成分的带通滤波器,如图5所示。
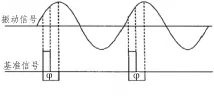
图4 不平衡振动信号相位提取原理图Fig.4 Principle diagram of Phase extraction for vibration signal caused by unbalance

图5 DFT等效带通滤波示意图Fig.5 Diagram of DFT equivalent band-pass filter
本系统一个周期内采样128点,采样间隔0.007 812 5T,T为转子周期。通过频谱分析提取基波分量X(1)。对于N点序列DFT变换对为:

在本系统中对动平衡提取的有用频率成份为基波分量,即令k=1。再对DFT进行蝶型运算可得到FFT,通过FFT直接计算基波分量,再计算得到不平衡量的相位,变换式后得:

最后可得相位:

φ1由于转子旋转方向、放大器相移、滤波器相移以及基准位置的影响与实际相位φ0相差φ′。因此对系统相位应进行精确标定。
4 结束语
本系统中锁相倍频的采样测量方法,实际上是硬件同步的测量方法。在基于TMS320F2812的硬件平台上,该方法精确度高,硬件电路简单易实现。实践证明,通过该方法本系统能准确地对振动周期信号实现整周期采样,为精确地获取不平衡量的幅值和相位提供了可靠的基础。本系统针对转速在9 300转/分以下的转子作动平衡测试,系统采用刚性转子影响系数法提取不平衡量,用DFT算法得出的不平衡量振幅和相位效果好。
[1]杜广宇,陈小桥,万中田.锁相倍频和准同步采样法在谐波测量中的应用[J].武汉大学学报,2001,34(5):39-44.
DU Guang-yu,CHEN Xiao-qiao,WAN Zhong-tian.Application of phase lock multiple frequency synchronous sampling and quasi-synchronous sampling to measurement of harmonics[J].Journal of Wuhan University of Hydraulic and Electric Engineering,2001,34(5):39-44.
[2]白志刚,唐贵基.一种转子动不平衡信号幅相特征的提取方法[J].电力科学与工程,2002,(4):69-70.
BAI Zhi-gang,TANG Gui-ji.Method of obtaining magnitude and phase of unbalanced signals for rotors[J].Electric Power Science and Engineering,2002,(4):69-70.
[3]王勤,杜垚,张键.锁相环电路在检测技术中的应用[J].计算机与数字工程,2009(10):186-189.
WANG Qin,DU Yao,ZHANG Jian.Application of phase lock loop in the detection technology[J].Computer&Digital Engineering,2009(10):186-189.
[4]肖敏.幅值和相位的精确测量及转子动平衡方法研究[D].汕头:汕头大学,2004.
[5]卢文祥,杜润生.机械工程测试·信息·信号分析[M].武汉:华中理工大学出版社,1991.
[6]陈长征,胡立新.设备振动分析与故障诊断技术[M].北京:科学出版社,2007.

