重载摆角铣头模态分析与实验研究
蔡力钢,马仕明,赵永胜,刘志峰,郭铁能
(北京工业大学 精密超精密加工国家工程研究中心,北京 100124)
重载摆角铣头是重型五轴联动数控机床的重要功能部件,通过铣头主轴的旋转和摆动,可以实现数控机床的五轴联动加工。重载摆角铣头相关技术的引进、消化、吸收和再创新,是我国高档重型数控机床急需解决的问题。目前,国产的摆角铣头大多是高转速、小扭矩电主轴结构,一般用于轻载、高效加工。本文研究的摆角铣头为机械式主轴结构,具有回转和摆动双传动链、大功率、大扭矩和结构紧凑等特点,主要用于钢、铁、钛合金等高硬度、难加工材料的大型复杂曲面零件加工,如三峡工程水轮发电机的大型叶片、大型船舶推进器、核电站核岛关键零件和大型汽车覆盖件模具等特殊零件的加工。铣头主轴系统与刀柄-刀具相连,其动态特性直接影响机床加工精度。因此,为有效提高高档重型数控机床的加工性能,有必要对其重载摆角铣头的动力学特性和相关实验等关键技术进行研究,为重载摆角铣头的自主研发与技术创新提供理论与实验支持。
目前关于模态分析的研究主要集中在模态参数辨识方面,比较有代表性的有KROMULSKI等[1]对工作变形(ODS)测定中的两种实验模态分析方法的应用进行了介绍,一种是测量正在运行的机器上测点的振动,另一种方法是基于机器的模态模型,包括工作过程中产生的力和振动的工作变形。Massa[2]提出了模糊模态分析的新概念和实验行为的预测。Pintelon等[3]对模态分析中的不确定性计算进行了研究,此处模态参数辨识是结构对摄动的响应。刘军等[4]进行了改进锤击法试验模态分析技术的研究,自主开发了信号采集和分析系统,并探讨了单点激励多点三向量响应模态试验分析方法来获得结构的完整模态振型的优点。在模态分析的应用研究上,Liu[5]对单一应变传感器、Jang[6]对硬盘驱动器、巨丽[7]对对击式液压锤进行了模态分析。而在对铣头类功能部件的模态分析中,只有作者在文献[8] 中进行了阐述,但当时没有进行实验验证。机床及其功能部件的动态特性尤其模态分析研究中,刘阳等[9]对某一卧式数控机床整机进行了模态分析和激振试验,并且充分考虑了直线滚动导轨结合面参数对机床动态特性的影响。张广鹏等[10]基于结合面动态基础特性参数,研究了机床导轨结合部动态特性的建模解析方法,并将其应用于机床整机动态特性解析。以上基本都是针对模态参数识别来展开研究,本文以重型龙门数控机床上的重载摆角铣头为研究对象,既研究其模态参数识别又研究其模态的建模和理论分析,并进行分析比较,给出铣头模型需要进行改进的途径。
本文以机械动力学、弹性力学及机械振动为理论基础,采用多约束方式下理论分析与实验验证相结合的综合研究方法,进行铣头和箱体特性的数字化建模、仿真计算和模态参数辨识,研究成果已在某重型机床企业的国产化重载摆角铣头的自主研发及其优化设计中应用。
1 重载摆角铣头结构
铣头主要由箱体、箱体左右端盖、主轴系统、摆动轴和两条由齿轮传动组成的传动链构成。铣头可以绕Z轴旋转运动,主轴系统还可以绕Y轴正负90°摆动,即B/C摆角铣头,其结构如图1所示。铣头主运动为齿轮传动,主轴为机械主轴,主运动通过两对直齿轮和两对等高齿螺旋伞齿轮传递到铣头主轴,铣头进给运动也为齿轮传动,电机通过齿轮降速将扭矩传给摆动轴,使摆动轴产生扭矩和转速,摆动轴采用两套交叉滚子轴承,克服摆动轴在摆动进给时承受切削产生的轴向、径向力及摆动运动产生的倾覆力矩,保证进给运动有足够的刚性。

图1 铣头结构Fig.1 Milling head structure
2 研究方法
模态综合比较验证研究方法是集自由悬挂、实际工况两种约束方式下的理论分析和实验验证相结合的研究方法。其目的是得到铣头准确的模态特性及其影响因素。理论分析中铣头在自由悬挂和实际工况两种约束下可相互进行比较,再和实验结果进行比较验证,如结果比较误差较大,则分析误差产生的原因,调整约束方式和重新进行校核实验,直到得到准确的铣头模态特性结果及其影响因素,用于铣头的结构改进和优化设计。研究方法框图如图2:

图2 模态综合比较研究方法Fig.2 Integrated research method for mode comparing
3 理论模态分析
3.1 铣头和箱体有限元建模
箱体是重载摆角铣头里尺寸、重量最大的零件,其固有特性对整个铣头的动态特性有重要影响,故首先对箱体进行有限元计算。箱体是三维非对称复杂实体模型,在保证模型求解收敛和计算量小的前提下,选择了三维实体单元对其进行自由网格划分。未经简化的重载摆角铣头箱体实体模型如图3所示,有限元模型网格划分如图4所示,钢丝绳吊起箱体的有限元模型(见4.2节)图9所示。四根钢丝绳仿真时用link10单元来模拟,钢丝绳的半径为10 mm,刚丝绳最上端全约束,钢丝绳与箱体连接处进行节点耦合。摆角铣头有限元模型数据如表1所示。

图3 实体模型Fig.3 Solid model

图4 有限元模型Fig.4 Finite model

表1 箱体及钢丝绳有限元模型参数Tab.1 FEM Parameters of box and steel wire
3.2 铣头理论模态计算结果与分析
箱体的模态计算以自由悬挂和原装固定两种方式进行。箱体自由悬挂即钢丝绳吊起箱体的情况可以和后面的实验对照,根据实验时吊起箱体所用绳子的类型和尺寸在仿真时进行其建模,这样理论与实验对比的方法可以更加准确了解箱体的固有特性。理论计算情况下,绳子吊起箱体和箱体实际工况两情形也可以进行相互比较验证,但此时不要把绳子的固有特性掺杂进来。箱体用绳子吊起仿真时的前三阶振型如图5所示,箱体上端全约束的前三阶振型如图6所示,箱体前六阶频率如表2所示。

表2 箱体前六阶频率Tab.2 The first six inherent frequency of box

图5 箱体吊起计算振型图Fig.5 Vibration mode of box with steel wire

图6 箱体上端全约束计算振型图Fig.6 Vibration mode of box with constraint
从箱体的阵型和模态动画上可以看出,箱体吊起情况和箱体全约束情况阵型类似。前三阶情况都是箱体上端几乎不动,一阶时箱体的两耳环相向张合弯曲,二阶时箱体的两耳环前后反向摆动,三阶时两耳环同时左右摆动;箱体的耳环处振幅较大,为刚度较薄弱环节,其影响因素为与此处几何尺寸有关,可以改变几何尺寸来提高其刚度,对箱体的进一步结构修改和优化提供参考。两者的一阶频率都在650 Hz以上,而此箱体的工作环境主轴转速最高3 000 r/min,远在工作频率范围之外,不会发生箱体共振现象。
得到箱体的固有特性后,把箱体内部的齿轮传动系统、主轴、摆动轴加入铣头中,计算整个铣头的固有特性,即铣头装配体特性。对于铣头内零件和零件间没有相对运动时,在软件里采取了glue操作,建立各零件间关系。有相对转动的零件间应在两零件有限元模型接触面对应节点处建立刚度和阻尼,也就是结合面参数确定问题,此处可能是线性也可能是非线性的刚度和阻尼,此处需要进行结合面的建模、辨识和实验,如建模、辨识和实验不理想,所得到的界面刚度和阻尼数据不可靠。结合面特性研究目前也是作者所在课题组正在研究的重要课题,目前还在研究过程中,待研究、辨识得到准确的铣头类零部件间结合面参数时,会把刚度和阻尼应用到本文研究的铣头装配体中。综合考虑铣头各部件对铣头固有特性的影响,此时也是铣头实际工作状态下所表现出的固有特性,其频率和阵型对铣头的设计、制造和使用都具有重要参考意义。铣头前三阶振型如图7所示,铣头前六阶频率如表3所示。

图7 铣头振型图Fig.7 Vibration mode of milling head

表3 铣头前六阶频率Tab.3 The first six inherent frequency of milling head
和箱体比较,质量的增加,导致铣头的一、二阶频率下降。一阶时铣头整体左右摆动,二阶时铣头前后摆动,高阶扭曲、张合明显;变形最大地方出现在铣头整体下端耳环和刀柄及轴承座附近。
4 模态实验研究
4.1 模态测试原理及方法
运用实验模态分析方法,和计算所得的模态特性加以比较,验证理论模型的正确性,为理论模型的修改提供依据。模态分析测试系统由三部分组成,即激励系统,测量系统和信号处理系统[11]。根据铣头的特点,本试验测试分析系统如图9所示。
对于铣头系统在激励力作用下的振动微分方程中的铣头位移列阵x可以看作是铣头系统固有频率的叠加,即:
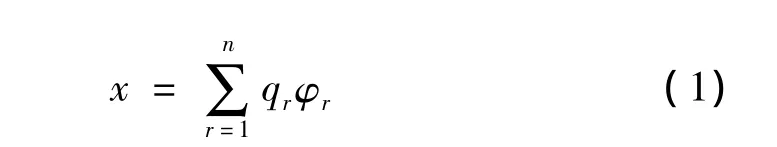
式中,qr为矢量x从物理坐标系转换到模态坐标系中的坐标,φr为第 r阶模态振型。由铣头动力学方程和方程(1)可以得到铣头在激励力作用下的频响函数:

式中 kr,cr,mr——铣头系统在第 r阶的模态刚度、阻尼和质量。
考察频响函数的一列:

由式(3)可知,频响函数的任一列包含全部的模态参数。如果在铣头某一点处激励,而在其他点拾振,便能得到频响函数的一列。由频响函数经傅里叶逆变换得到系统的脉冲响应从而识别系统的模态参数[2]。
铣头工作状态下,在其箱体上选取一个参考点,将该参考点响应信号作为参考信号。参考信号与其他各测点响应信号可以求得互谱密度函数,对互谱密度函数进行傅里叶逆变换得到互相关函数。由于互相关函数方程与系统的脉冲响应函数方程有相似的形式,都能表示成一系列衰减正弦函数的和,而且每个衰减正弦都有一个固有频率和阻尼比与结构的各阶模态相对应,振型矢量的位置也相同,因此互相关函数能够被用作脉冲响应函数来识别模态参数[6,12]。
4.2 模态测试结果与分析
本次模态实验采用丹麦B&K公司的模态测试分析系统进行,主要测试设备包括:4507型加速度传感器、力锤和信号采集器等,将测量的频响函数数据导入ME'scopeVES软件,并在ME'scopeVES中进行模态参数识别。目前常用的支承方式有三种:自由支承、固定支承和原装支承。由于测试地点是在工厂现场,实验条件比较简单,选择自由支撑作为支承方式,将摆角铣头壳体用钢丝悬挂起来,如图8所示,此种支承方式常用且效果较好。。选择钢丝绳的长度时,考虑了绳锁的频率要至少低于箱体本身的频率五分之一,这样才能保证自由悬挂状态下箱体的模态特性测试的准确性。

图8 现场测试的箱体Fig.8 Box under testing

图9 箱体模型测试系统图Fig.9 Test system of box model
箱体模型测试原理图如图9所示,由于箱体结构比较大,传感器的移动和布置比较方便,本次模态实验的激励方式选择单点激励多点测量的测试方法,激励点选在左侧耳环较下方处,此处为薄壁,较容易把铣头激振起来,以便得到较好的响应信号。为了利用最少的测量次数得到最多的振型自由度,选择了移动锤击激励,选取了2个不同的激励点,最下方激励点方向沿着Y轴方向进行,较上端激励点方向沿X轴方向进行。每次实验过程中保持激励点的位置不变,只改变响应点的位置,同时记录激励力和加速度响应信号。从图8中可以看到,箱体主要由两个承载主轴部件的悬吊耳环和用于装卡到滑枕上的刚度较大壳体组成,由于悬吊耳环是主要承载摆动轴部件及切削力的箱体中主要部分,并且结构相对薄弱,所以在悬吊耳环布置了较多的测点,箱体上端也分布少量测点,测点(即传感器粘贴点)和激励点为图中的圆圈处,图中把两个激励点列出,而没有列出所有测点,图中箱体背面也有测点。
箱体测试结果的阵型图如图10所示,由于是在两个激励点进行的激励,且分别沿X、Y方向,其目的是把箱体各阶振型都激励起来,并拾取到,一阶和三阶阵型沿Y方向运动趋势,为Y向激励点激励所产生的振型;二阶时两耳环前后反向摆动,即沿X方向运动,为X向激励点激励所产生的振型,且此三阶阵型已和有限元分析的前三阶模态频率和模态阵型吻合较好。前六阶频率如表4所示:
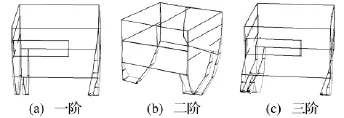
图10 箱体测试阵型Fig.10 Testing vibration mode of box

表4 箱体前六阶测试频率Tab.4 The first six testing frequency of box
铣头整体实验是铣头正常安装在五轴数控机床上进行的,即铣头的支撑方式为原装固定支撑。本次模态实验的激励方式同样选择单点激励多点测量的测试方法。即在实验过程中保持激励点的位置不变,只改变响应点的位置,同时记录激励力和加速度响应信号。锤击点选为刀尖处激励,在同一点处分别沿X方向和Y方向进行激励,如图11所示为摆动轴摆动到90°时,沿 Y轴进行激励的现场图。

图11 现场测试铣头Fig.11 Milling head under testing
其前三阶振型如图12所示,第一阶和三阶为Y向激励所得振型图,二阶为沿X向激励所得振型图,振型图前六阶测试频率如表5所示:

图12 铣头测试振型Fig.12 Testing vibration mode of milling head

表5 铣头前六阶测试频率Tab.5 The first six testing frequency of milling head
5 理论与试验模态结果分析比较
5.1 箱体本身的比较
测试和理论计算的箱体前六阶固有频率如表6所示,箱体频率比较图如图13所示。实验所得频率和理论计算频率误差在13%以内,故可以认为其前六阶的固有频率是可信的。尤其比较关心的一阶频率误差仅为 7.9%。
一阶时两耳环沿Y向张合,二阶时两耳环沿X反向摆动,三阶时整体沿Y向摆动,高阶扭曲、张合明显,文中所提到的X、Y、Z向均是指机床坐标方向。变形最大地方出现在箱体两耳环处,尤其摆动链方向的耳环变形明显。分析其原因为,摆动链一侧耳环的结构尺寸较小,即耳环厚度较小,从而导致刚度较低。但深入研究其影响因素,箱体的频率和振型与箱体的质量分布也有关系,但从箱体要求结构紧凑的特点来看,在箱体材料不变的情况下,箱体的质量主要集中在箱体上端,下端为质量分布较少的安装摆动轴的中空耳环,此种情况导致耳环处刚度较低,可以通过适当调整铣头和箱体的质量分布、增加耳环的厚度等方式改善耳环处相对薄弱的问题。

表6 箱体前六阶频率和误差Tab.6 The first six frequency and error of box
由于机床的最高转速为3 000 r/min,即最高工作频率是50 Hz,而箱体的最低固有频率即一阶实验频率为573 Hz,远大于其最高工作转速频率,故铣头箱体的整体动态特性较好,不会有共振现象发生。
5.2 从箱体到铣头整体的比较
铣头整体的第一阶固有频率为477 Hz,第一阶模态振型除整体表现为沿Y方向的摆动,铣头整机的左侧耳环处振动相对比较强烈。第二阶的固有频率为493 Hz,第二阶模态振型铣头整体表现为沿X方向的摆动,高阶已经有扭曲趋势。可以看出铣头整体的左右两侧的悬吊耳环处振动相对比较剧烈。铣头前6阶频率和误差如表7所示,铣头频率比较图如图14所示。
从振型图上可以看出,在加入箱体的左右端盖、摆动轴、主轴系统和里面的齿轮传动系统等零件后,箱体耳环处的振幅与单独分析箱体比较有所降低,但仍然是薄弱部位之一。此时,另一处薄弱部位为主轴前端,由于主轴前端向外伸长,距离铣头上端约束处较远,故主轴前端也表现出刚性较差,振幅较大的现象。在主轴不变的情况下,可以考虑采取增加主轴前端轴承刚度、改变轴承预紧力和提高刀柄刚度等措施来提高主轴前端刚度,从而可提高机床的加工精度。

图13 箱体频率比较图Fig.13 Contrast of box frequency
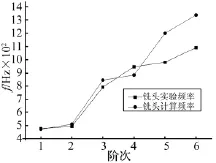
图14 铣头频率比较图Fig.14 Contrast of milling head frequency

表7 铣头前六阶频率和误差Tab.7 The first six frequency and error of milling head
6 结论
为了掌握重载摆角铣头的模态特性及其影响因素之间的关系,提出了一种多约束方式下的理论分析与实验验证相结合的多渠道相互比较与验证的综合研究方法,通过对铣头箱体和铣头整体进行了多种方式约束下的模态计算、仿真、实验以及相互比较分析和验证,证明了该方法的有效性,得到了铣头准确的模态特性及其影响因素。研究结果为重载摆角铣头结构优化设计和改进提供理论与实验依据。主要结论如下:
(1)从理论与实验测试结果分析方面看,理论计算和实验测试结果吻合较好,尤其对于铣头整体,实验和计算的一阶频率误差仅为1.06%;对于箱体计算和测试的误差相对较大,但一阶频率误差也仅在8%之内,理论计算时由于考虑了自由支撑和原装固定(铣头上端全约束)两种形式,而且两种形式都是经过多次计算直至收敛的结果,计算误差仅为2.24%。因此,经过多种方式的验证,较好的认识了铣头的动态特性。
(2)从铣头振动频率上看,重载摆角铣头箱体的一阶频率为600 Hz左右,铣头整体的一阶频率为470 Hz左右,随着质量的增加,频率下降21.7%,但远在机床工作频率50 Hz左右之外,故铣头及箱体从振动频率上看动态性能较好。
(3)从铣头薄弱环节上看,根据模态阵型和变形云图可知,箱体的左耳环(摆动链方向耳环)相对较薄弱,振动趋势较明显,需要进一步对箱体进行结构改进,应首先从此处着手考虑。其次为主轴前端有较大振动,建议增加轴承刚度和选择刚度较好的刀柄系统等措施来降低主轴前端的振动量。
[1] Kromulski J,Hojan E.An application of two experimental modal analysis methods for the determination of operational deflection shapes[J] .Journal of Sound and Vibration,1996,196(4):429-438.
[2] Massa F,Tison T,Lallemand B.Fuzzy modal analysis:prediction of experimental behaviours[J] .Journal of Sound and Vibration,2009,322:135 -154.
[3] Pintelona R, Guillaumeb P, Schoukens J. Uncertainty calculation in(operational)modal analysis[J] .Mechanical Systems and Signal Processing,2007,21:2359 -2373.
[4] 刘 军,高建立,穆桂脂,等.改进锤击法试验模态分析技术的研究[J] .振动与冲击,2009,28(3):174 -177.
[5] Liu C,Cui T,Zhou Z.Modal analysis of a unimorph piezoelectrical transducer[J] .Microsystem Technologies,2003,9:474 -479.
[6] Jang G H,Han JH,Seo CH.Finite element modal analysis of a rotating disk-spindle system in a HDD with hydrodynamic bearings considering the flexibility of a complicated supporting structure[J] .Microsyst Technol,2005,11:488 - 498.
[7] 巨 力,李永堂.对击式液压锤理论与试验模态分析[J] .机械工程学报,2009,45(1):273 -281.
[8] 马仕明,杨文通,刘志峰,等.基于ANSYS的大型数控机床大扭矩、大功率B摆角铣头模态分析[J] .机械设计与制造,2008,4:156 -158.
[9] 刘 阳,李景奎,朱春霞,等,直线滚动导轨结合面参数对数控机床动态特性的影响[J] .东北大学学报(自然科学版),2006,27(12):1369 -1372.
[10] 张广鹏,史文浩,黄玉美.机床导轨结合部的动态特性解析方法及其应用[J] .机械工程学报,2002,38(10):114-117.
[11] 韩邦成,张姝娜,房建成,等,磁悬浮反作用飞轮系统模态分析及试验研究[J] .系统仿真学报,2008,20(3):763-766.
[12] 郑 敏,申 凡,史东峰,等.单独利用响应数据进行模态分析[J] .中国机械工程,2006(4):405-409.
[13] Kim S G,Jang S H,Hwang H Y,et al.Analysis of dynamic characteristics and evaluation of dynamic stiffness of a 5-axis multi-tasking machine tool by using F.E.M and exciter test[C] //International Conference on Smart Manufacturing Application.KINTEX,Gyeonggi-do,Korea:IEEE,2008:565-569.

