管材参数对输液管流固耦合振动的影响
杨 超,范士娟
(华东交通大学 载运工具与装备省部共建教育部重点实验室,南昌 330013)
输液管系统中存在液体压力脉动和管壁结构振动,它们之间的耦合作用,会造成噪声污染,严重的耦合振动可导致灾难性事故。近几年,我国城市供水管道爆裂事故频频发生,且有明显上升的趋势。2004~2008年间,上海浦东地区大口径(DN≥500 mm)爆管24次[1]。另据报道,大连市在2007年11月,6天爆管81起;南昌市在2004年12月,从26日开始,平均每天爆管达35次以上,直径300 mm以上的有18处,爆管最大直径超过 1 000 mm 的有 2 次;天津[2]、常州[3]、深圳、武汉等城市和地区都发生过多起供水管道爆裂事故,造成了大量的水资源浪费。管道与水之间极端的流固耦合作用——“水锤”是引起供水管道爆裂事故的重要原因之一[4]。政府每年需要大笔费用来维护供水系统,如美国亚特兰大,未来10年共需约40亿美元用于供水系统和排污系统的改造[5]。因此,研究输液管系统流固耦合(fluid-structure interaction,简称FSI)振动的规律及相关参数对耦合振动的影响,为输液管系统的设计和改造提供依据,具有现实的必要性。金基铎[6]、包日东[7]、荆洪英[8]分别研究了不同支承(约束)条件下输流管道临界流速和稳定性问题,Jiang[9]用数值方法研究了管壁厚度及剪切模量对地下管道动应力和应变的影响,Zhao[10]、马飞[11]、穆祥鹏[12]、陈彬[13]对水击耦合振动响应及其特性进行了研究;但他们都未研究输液管道直径、结构阻尼等参数对管道系统响应的影响及程度。本文以RPV(蓄水池-管道-阀门)系统这一典型的输液管道系统为对象,研究管道结构参数对其流固耦合振动响应的影响,暂不研究管道的稳定性问题。
1 输液管道耦合振动模型及计算方法
1.1 输液管道轴向耦合振动模型
忽略水的压缩性,水作一维流动,管道在弹性范围内作小幅振动,管道与水之间的阻尼为比例阻尼,忽略重力的影响,则两端支承非恒定流输水管道的流固耦合振动方程为[14]
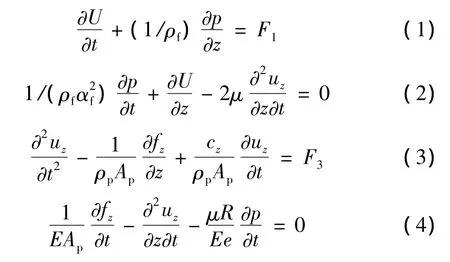
式中,uz为管道在z方向(轴向)的振动位移(m);fz为管道在z轴方向的内力(N);cz为管道在z轴方向的结构阻尼系数(N·s/m);p、U分别为水压力(Pa)和水截面平均流速(m/s);E、R、e、ρp、Ap、μ 分别为管材弹性模量(Pa)、管道内半径(m)、管道壁厚(m)、管材密度(kg/m3)、管壁截面积(m2)、管材泊松比;f为水与管道壁之间的摩擦系数;ρf、Af、af分别为水密度(kg/m3)、水横截面面积(m2)和液体压力波速(m/s);vr表示水与管道的相对速度(m/s)
1.2 流固耦合振动数值计算方法
用于描述输水管道流固耦合振动的运动方程(1)~(4)是偏微分方程组,通常无法求得其解析解,只能进行数值计算。对于线性、拟线性系统而言,特征线法(MOC)是一种将偏微分方程(组)转换为常微分方程(组)的有效工具,通过数值计算便可获得原方程组的数值解。
方程(1)~(4)经过特征线法变换后,得到常微分方程组:

以差分格式将式(5)、式((6)展开并整理,可得特征线差分方程组,写成矩阵形式,有:
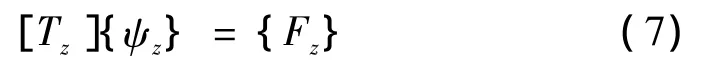
式中,[Tz] 、{ψz}、{Fz}分别为方程组的系数矩阵、数值计算点未知量向量和已知力向量。
2 轴向耦合振动数值计算与分析
大直径输液管道发生流固耦合振动时,危害较大,故本文以大直径蓄水池-直管-阀门系统作为研究对象,系统如图1所示。水以U=1 m/s的速度从蓄水池流向阀门,管道可沿轴向自由运动。蓄水池压头H=20 m,管长 L=20 m,水体积模量 Kf=2.1 GN/m2,水密度 ρf=1 000 kg/m3,水摩擦系数 f=0.002,阀门后压力为0 Pa,阀门突然关闭。

图1 蓄水池-管道-阀门系统示意图Fig.1 Sketch map of reservoir-pipe-valve
所有仿真计算的基本条件:阀门突然关闭,仿真计算采样长度2 s,阀门处管道轴向自由。
2.1 管道结构阻尼对响应的影响
管外径D=813 mm,管壁厚e=8 mm,管壁弹性模量 E=210 GN/m2,管壁密度 ρp=7 900 kg/m3,泊松比μ =0.3,水摩擦系数 f=0.002,管道结构阻尼系数 cz取不同值时阀门处液体压力、管壁振动速度在2 s内的计算结果示于图2、图3。
cz=0、cz=0.000 5 和 cz=0.005 时液体压力曲线和管壁振动速度曲线如图4、图5所示(图中的曲线a、b、c分别为 cz=0、0.000 5 和 0.005 时的结果)。
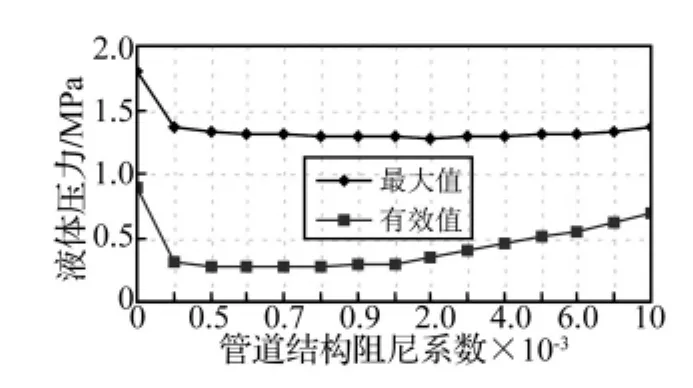
图2 阀门处液体压力响应Fig.2 Responses of fluid pressure at valve
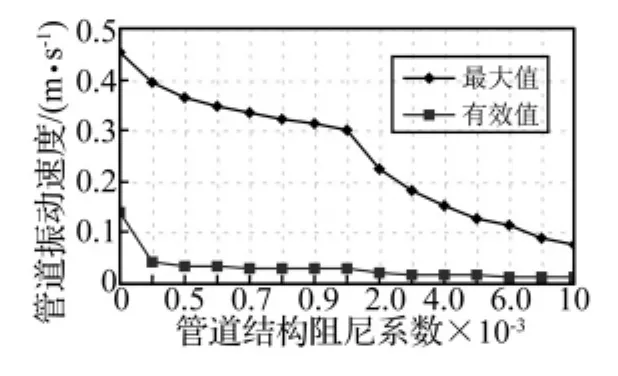
图3 阀门处管壁振动速度响应Fig.3 Responses of pipe vibration velocity at valve
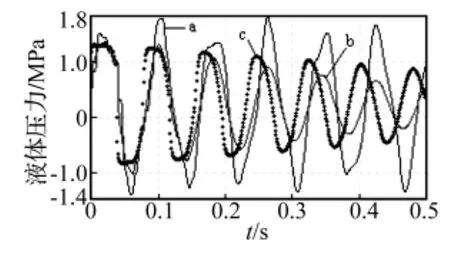
图4 阀门处液体压力响应Fig.4 Responses of fluid pressure at valve
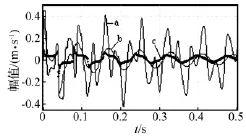
图5 阀门处管壁振动速度响应Fig.5 Responses of pipe vibration velocity at valve
从图2~图5中可以看到,① 忽略管道结构阻尼(cz=0)时,液体压能和管壁振动的能量都较大;从图4及图5中还可以看到,由于液体阻尼的作用,液体压力响应中的高频成分不明显,以水静压力为平衡位置作缓慢衰减振动,主要振动频率为12.51 Hz,对应FSI压力基波;而管壁振动速度响应中的高次谐波成分非常明显,主要包含三个谐波成分,频率分别为12.51 Hz、31.52 Hz和55.04 Hz。② 考虑管道结构阻尼时,液体压力响应和管壁振动速度响应中的高阶谐波成分很快消失,只有12.51 Hz的基波成分,因此,在供水系统中,只要使水流的压力脉动频率避开FSI压力基频,就可防止共振的发生。随着管道结构阻尼系数的增大,管壁的振动强度不断减小,而液体压力的有效值则是先减小(cz≤0.000 7),后增大(cz>0.000 7),但变化幅度较小;但当cz>0.001时,液体的压能快速增加。
随着管道结构阻尼的增大,管壁本身的振动受到抑制,分担的振动能量越来越小,当管道结构阻尼大于某一值时,系统的振动能量主要集中在液体里,造成液体压力能的升高。
2.2 管材泊松比对响应的影响
管道参数:D=813 mm,e=8 mm,E=210 GN/m2,ρp=7 900 kg/m3,忽略所有摩擦因素,管材泊松比μ分别取0.25、0.3、0.35、0.4 和 0.45。阀门处液体压力、管壁振动速度的最大值和在2 s内的有效值示于表1。
可以看到,考虑泊松耦合效应后,随着泊松比的增大,液体压力的最大值和有效值均增大,而且有效值增幅较快;管壁振动速度的最大值和有效值略有减小,但幅度不大。
液体的冲击引起管壁的振动和液体压力波动,管壁的振动反过来又影响着液体的压力波动,彼此耦合,管壁与液体分担系统的振动能量。在管道轴向自由的条件下,泊松耦合效应将管壁的部分振动能量转换成液体压能,使液体压能增大,管壁振动强度减少,泊松比越大,管壁的“呼吸”运动就越显著,能量转换也越多,更多的管壁振动能量被转换成液体的压力能——泊松比起能量转换器的作用。

表1 不同泊松比条件下的数值计算结果Tab.1 Numerical results with different Poisson’s Ratio
2.3 管道壁厚对系统响应的影响
管道参数:D=813 mm,E=210 GN/m2,ρp=7 900 kg/m3,μ =0.3,cz=0,壁厚分别取 8 mm ~30 mm,间隔2 mm。液体摩擦系数f=0.002,管道壁厚不同时阀门处液体压力、管壁振动速度的最大值和在2 s内的有效值分别示于图6、图7。
从图6和图7可以看出,在管道外径不变的情况下,水击发生后,液体压力的有效值(液体的压力能)随着管道壁厚的增大而增大,而管壁振动速度的有效值(振动强度)随着管道壁厚的增大而减小。这是因为,随着管道壁厚的增大,管壁轴向刚度增大,液体对管壁轴向冲击时,更多的冲击能量反弹回到液体里,造成液体压力能的增大,而管壁轴向振动强度则向减弱的方向变化;如果管壁刚度很大,水击振动情况与管端固定的情况类似,管壁轴向振动很小,而液体压能随液体流速急剧升高。
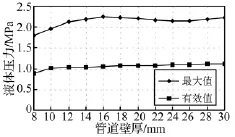
图6 阀门处液体压力响应Fig.6 Fluid pressure at valve
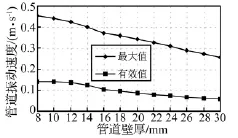
图7 阀门处管道振动速度Fig.7 Pipe vibration velocity at valve
3 结论
通过前面的计算和对比分析,对于文中的RPV系统,可以得出以下结论:
(1)液体摩擦阻尼对液体压力响应中高频成分的影响大,对管壁轴向振动响应中高频成分的影响小;
(2)随着管道结构阻尼的增大,管壁本身的振动受到抑制,分担的振动能量越来越小,当管道结构阻尼大于某一值时,系统的振动能量主要集中在液体里,造成液体压力能的升高;
(3)随着管壁材料泊松比的增大,液体的压能增大,管壁的轴向振动强度降低;
(4)管道外径不变时,随着管道壁厚的增大,液体的压能增大,管壁的轴向振动强度减小。
[1] 范晶璟.供水管网爆管分析及预防对策[J] .上海水务,2009,25(1):21-22.
[2] 张铁刚.天津市供水管网爆管折管分析及降漏对策研究[D] .西安:西安建筑科技大学,2006.
[3] 陈 欣.常州市大口径输水钢管爆管原因及对策研究[D] .上海:同济大学,2007.
[4] 金 锥.停泵水锤及其防护[M] .北京:中国建筑工业出版社,2004.
[5] Bruce G.Kuffer.Emerging use of plastic(HDPE)pipe in dynamic municipal water systems and trenchless technologies for improved infrastructure performance[C] .Pipelines 2009:Infrastructure's Hidden Assets,Proceedings of the Pipelines 2009 Conference,ASCE,2009:679 -688.
[6] 金基铎,杨晓东,张宇飞.固定约束松动对输流管道稳定性和临界流速的影响[J] .振动与冲击,2009,28(6):95-99.
[7] 包日东,金志浩,闻邦椿.一般支承条件下输流管道的非线性动力学特性研究[J] .振动与冲击,2009,28(7):153-157,186.
[8] 荆洪英,金基铎,闻邦椿.一端固定具有中间支承输流管道临界流速及稳定性分析[J] .机械工程学报,2009,45(3):89-93.
[9] Jiang L F,Chen S X,Xu X C.Dynamic response of underground pipeline to incident body waves[C] .ICPTT 2009:Advances and Experiences with Pipelines and Trenchless Technology for Water, Sewer, Gas, and Oil Applications,Proceedings of the International Conference on Pipelines and Trenchless Technology, ASCE, 2009:325-334.
[10] Zhao M,Ghidaoui M S.Efficient quasi-two-dimensional model for water hammer problems[J] .Journal of Hydraulic Engineering,2003,12:1007-1013.
[11] 马 飞,曲世琳,吴一民 .给水管网非恒定流动数值计算方法[J] .北京科技大学学报,2009,31(4):423-427.
[12] 穆祥鹏,练继建,刘瀚和.复杂输水系统水力过渡的数值方法比较及适用性分析[J] .天津大学学报,2008,41(5):515-521.
[13] 陈 彬,刘 阁.液压换向阀的耦合水击振动特性研究[J] .实验力学,2009,24(1):73-79.
[14] 杨 超.非恒定流充液管系统耦合振动特性及振动抑制[D] .武汉:华中科技大学,2007:19-38.

