预应力引起的曲线箱梁桥支座反力与位移研究
黄 超,谭长瑞,段 鹏
(1.重庆交通大学土木建筑学院,重庆400074;2.北京中桀伟业道路工程技术有限公司,北京100101;3.重庆建筑工程职业学院,重庆400039)
1 曲绕箱梁桥的病害
随着我国城市规模不断增大,道路交通逐渐成为制约城市发展的主要因素之一。为了在有限的地理空间上建立起顺畅的交通系统,许多城市修建了各种高架桥、互通式立交工程。曲线箱梁桥以其良好的地形适应性和对城市景观的美化效果,成为了高架桥或者立交工程的主要结构形式。在工程实践中,曲线梁桥也表现出了各种病害,参考国内外已出现的曲线梁桥事故,可总结为如下四种常见病害。
1.1 梁体向外侧移和翻转
由于“弯-扭耦合”效应,曲线梁在荷载作用下绕某一轴线旋转,产生水平面和竖平面位移,例如深圳市华强立交A匝道第三联在投入使用两年后,曲线梁桥突然向外移动和向外侧翻转,曲线梁体径向最大位移为47 cm,切向最大位移为16 cm。
1.2 固结墩墩身开裂
对于某些曲率半径较小的连续曲线梁桥,在设计中为了控制跨中梁体的侧向变形,将中间墩设置为墩梁固结墩,或者在中间墩处设置侧向限位装置。在预应力、温度、汽车离心力等荷载的作用下,中间墩支座承受较大的水平反力,墩身出现水平裂缝,当这种水平力较大时,甚至造成中间墩破坏。
1.3 腹板内预应力筋崩出
预应力混凝土曲线箱梁桥在张拉纵向力筋时,预应力钢束产生的径向水平压力易使箱梁腹板超载,严重时造成腹板混凝土崩裂破坏,预应力钢束绷直并从腹板内崩出。
1.4 内侧支座脱空
曲线梁桥在竖向荷载作用下,内侧、外侧支座支反力相差较大,当汽车荷载偏载时,这种差异可能导致外侧支座超出承载能力极限而内侧支座承载能力尚未充分发挥的情况(偏载效应较大时内侧支座甚至出现拉力),即内侧支座脱空。
2 曲线梁桥的受力特性
由于存在平面曲率半径,同直线梁桥相比,曲线箱梁桥有着独特的受力特性。在自重、活载、预应力荷载以及温度荷载作用下,曲线梁桥产生弯矩的同时,伴随产生扭矩,反之,在产生扭矩时也会产生弯矩,即“弯-扭耦合”效应[1];在移动荷载作用下(移动的汽车荷载),曲线梁桥承受曲率平面内的离心力荷载。在结构变形方面,曲线梁桥在荷载作用下会产生水平面位移和竖平面位移,变形呈三维空间特性。预应力混凝土曲线箱梁桥中,预应力钢束线形为空间曲线,在预应力作用下,梁体为空间受力体系,其内力和变形分析十分复杂,本文拟采用数值分析方法,以重庆市某小区一座小半径曲线箱梁桥为背景,运用通用有限元软件ANSYS分析预应力引起的该桥内外侧支座反力差值与位移情况。
3 ANSYS 模拟预应力结构的基本原理[3]
ANSYS作为一款较成熟的大型通用有限元软件,近年来被越来越多的应用于土建工程领域,同模型试验相比,用ANSYS进行数值模拟可以显著的降低成本,而且能够模拟各种复杂的边界条件。ANSYS模拟预应力效应主要有两种方式:(1)等效荷载法:用一组“等效荷载”替代预应力筋的作用施加到结构上,该方法的优点是:建模简单,不必考虑力筋的具体位置,单元划分较灵活,其主要缺点是无法模拟张拉过程中引起的预应力损失,局部计算结果同实际情况相差较大;(2)实体力筋法:预应力筋和混凝土独立建模,力筋多采用LINK系列单元,混凝土采用SOLID系列实体单元,通过两种单元的节点耦合或者建立约束方程来模拟预应力效应,该方法可有效消除等效荷载法的缺点,可对预应力混凝土结构的应力分析进行精确模拟,但是该方法建模复杂,对计算机的系统配置要求高,且可能出现求解不收敛的情况,故该方法一般用于重要结构的局部分析,本文算例中,计算模型采用第二种方法建模,预应力效应通过初应变施加到结构上。
4 计算模型说明
本文算例中,桥轴线(箱梁中心线,不考虑横桥向坡度)半径R=45m,跨径30m,采用单箱双室截面,箱梁横截面尺寸详见图1。

图1 箱梁横截面
箱梁混凝土为C50,混凝土应力-应变关系采用《混凝土结构设计规范》(GB 50010-2002)中规定的曲线,即由抛物线上升段和水平线组成[2],上升段的数学表达式为:σc=fc[1-(1-εc/ε0)2],式中:fc为混凝土抗压强度设计值,文中取 fc=32.4 MPa,ε0=0.002。混凝土应力-应变关系曲线如图2所示。

图2 混凝土应力-应变关系
箱梁内预应力钢束规格为:15Φs15.2,内、中、外腹板各布置6束,钢束标准强度fpk=1 860 MPa,弹性模量:Ep=1.95×105MPa,锚下张拉控制应力:σcon=0.70 fpk=1 302 MPa。
文中预应力通过初应变施加于箱梁上,为简化建模,将内、中、外腹板的预应力钢束等效为三束,每束的初应变为:ε=σ/E=6.677×10-3,截面积为:A=15×139×10-6×6=1.251×10-2m2。钢束采用LINK8单元,混凝土采用SOLI65单元,钢束与混凝土之间的作用通过节点自由度耦合进行模拟,桥梁采用抗扭支座,0号墩为固结支座,1号墩为竖向、径向约束支座,模型求解时考虑材料非线性影响[4],全桥SOLID65单元共4 440个,LINK8单元共368个,全桥模型单元离散图如图3所示。

图3 模型单元离散图
5 数值分析结果及评价
5.1 内侧、外侧支座支反力分析
为了清楚反映预应力对支座支反力的影响程度,计算模型考虑两种工况,工况一:曲线箱梁仅承受预应力荷载;工况二:曲线箱梁承受预应力荷载与自重荷载。进行有限元模型求解,根据通用后处理器(post1)列出0号墩、1号墩内外侧支座在两种工况下的支反力如下表所示,表1为工况一下各支座反力,表2为工况二下各支座反力。表中竖向力方向以向上为正。
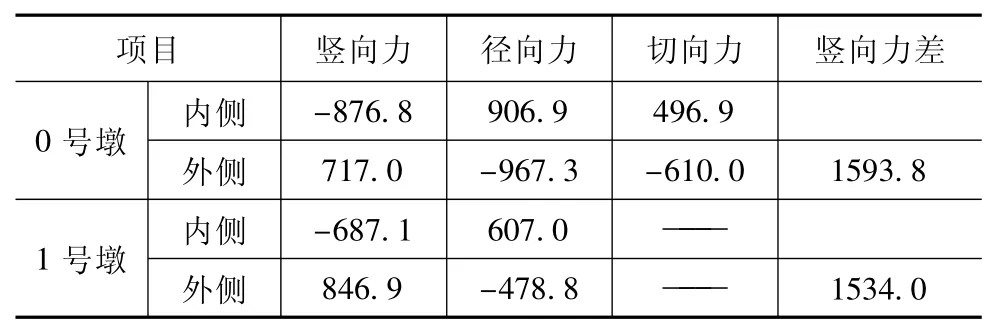
表1 预应力作用下的支反力(kN)

表2 预应力与自重共同作用下的支反力(kN)
通过上述两个表格可以看出:在预应力荷载单独作用下,曲线箱梁的外侧支座支反力值较大,内侧支反力为负,即支座处出现拉力(这与实际情况不符,其原因为在模型中支座处设置为竖向双向约束);在自重和预应力荷载共同作用下,内侧、外侧支座反力均向上,对比两种工况:预应力引起的竖向力差占总差值百分比为:η=1534/2599.7=59%,说明在恒荷载(模型中未考虑二期恒载和栏杆等附属设施的自重)作用下,预应力引起的内外侧支反力差值占总差值的主要部分。从表1和表2还可以看出,在预应力作用下,曲线箱梁桥支座处产生径向反力和切向反力,其中径向力远大于切向力,表明预应力引起的曲梁绷直的趋势较曲梁轴线压缩要强。
5.2 预应力荷载作用下曲线箱梁顶平面内缘、外缘位移分析
根据数值分析结果,绘制预应力荷载作用下曲线箱梁顶板内缘、外缘的竖向位移(u-z)、水平面内位移(u-xy)以及总位移向量(u-sum)图如图4、图5。
由图4、图5可以看出,在预应力作用下,曲线箱梁出现向上挠曲变形,外缘最大变形(竖向位移u-z)为9mm,内缘最大变形为13mm,梁体呈向外侧翻转趋势;曲线箱梁的变形以竖平面变形为主,外缘水平面位移叫内缘大,表明箱梁在预应力荷载作用下,横截面发生了畸变变形。

图4 外缘竖向位移

图5 内缘竖向位移
5.3 预应力与自重荷载作用下曲线箱梁顶平面内缘、外缘位移分析[5]
根据模型计算结果,绘制曲线箱梁在预应力与自重荷载共同作用下的位移如图6、图7所示。

图6 外缘竖向位移

图7 内缘竖向位移
从上图可以看出,在预应力和自重荷载共同作用下,曲线箱梁产生了水平面位移与竖平面位移,箱梁顶板内缘、外缘变形差值较小,对比5.2节中结论,可以看出自重荷载缓和了预应力荷载引起的箱梁翻转趋势。
5.4 结论及建议
(1)小半径曲线箱梁桥在预应力荷载作用下,内外侧支座均产生支反力,内侧为拉、外侧为压,且支反力差值为恒载产生支反力差值的主要部分;在水平面内,支座处产生径向约束和切向约束(径向、切向均约束的支座)。
(2)曲线箱梁桥在预应力作用下,梁体产生竖向和水平变形,其中竖向变形占主导部分,整个箱梁呈现向外侧翻转的趋势,自重荷载可在一定程度上消减箱梁内侧、外侧的竖向位移差值[6]。
(3)设有双支座曲线箱梁桥,外侧支座承受的竖向荷载较内侧支座大,设计时应考虑内、外侧支座采用不同型号,或者增大支座承载力储备值,以防止外侧支座已经被压坏而内侧支座的承载力尚未充分受力的情况[7]。
[1] 姚玲森.曲线梁[M].北京:人民交通出版社,1987:7-12
[2] 江见鲸.钢筋混凝土结构非线性有限元分析[M].西安:陕西科学技术出版社,1993
[3] 王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,1993
[4] 赵颖华,李秀文,徐进.两端简支超静定曲线梁横向位移解析分析[J].沈阳建筑大学学报,2005,21(3):189-191
[5] 程进,沈旭东.基于ANSYS预应力混凝土曲线梁桥三维施工仿真分析[J].公路交通科技,2007,24(4):108-112
[6] 金菊,王淑涛.中小跨径曲线梁桥半径变化对结构变形的影响分析[J].河北工业大学学报,2007,36(4):110-113
[7] 张蕊.曲线梁桥设计分析[J].公路工程与运输,2008,8(4):128-130

