基于改进免疫算法的有能力约束车辆路径问题
梁勤欧
(浙江师范大学地理与环境科学学院,浙江 金华 321004)
车辆路径问题(vehicle routing problem,VRP)是指为服务于需求已知的一组客户的车队,设计从中心仓库出发并返回的最小费用路径,约束条件包括客户只能被服务一次,且车辆的载重能力有限[1],或具有时间窗限制[2]等,并随约束条件的拓展可以衍生出许多新的问题。VRP自从1959年由 DANTZIG 和 RAMSER[3]提出以来,迅速成为运筹学、物流管理、交通规划管理、地理区位等领域的研究热点。VRP的研究属于组合优化中的NP难问题,即随着问题的规模增加,计算机求解所耗费的时间迅速增加。针对VRP的特点,国内外学者引入各种优化算法对其进行求解,其中应用较多的是各种智能算法,如遗传算法[4-5]、进化计算[6]等。
人工免疫系统(artificial immune system,AIS)是近年来兴起的一种新的智能计算方法[7]。免疫系统的记忆功能(疫苗)常被作为遗传算法种群更新中的一种机制而使用,以便改进遗传算法的性能[8]。传统的遗传算法在进行VRP求解时,常出现在局部最优解附近徘徊的问题[9-10]。应用免疫系统与遗传算法相结合的新算法进行VRP的研究,因其吸收了两种算法的优点,在研究效率上比传统的遗传算法有所提高。笔者在实验研究VRP初期,采用了免疫记忆功能与信息熵相结合的免疫遗传算法,结果出现计算量大且常早熟收敛的现象。基于以上问题,笔者提出了一种改进的免疫遗传算法,并通过有能力约束的VRP实验验证了该算法的有效性。
1 有能力约束VRP数学模型
有能力约束VRP一般描述为[11]:某一配送中心M(用i=0表示)有P辆车(p=1,2,…,P),需要配送的客户(或仓库)为 N(i=1,2,…,N)个,每辆车的载重能力为 Bp(p=1,2,…,P),客户的需求为qi(i=1,2,…,N),客户之间以及客户与配送中心的距离为 dij(i,j=1,2,…N)。VRP的优化目标是时间、距离和费用等运输成本最小。笔者以运输距离最短构造数学模型,首先定义变量如下:

则有能力约束的VRP数学模型如下:
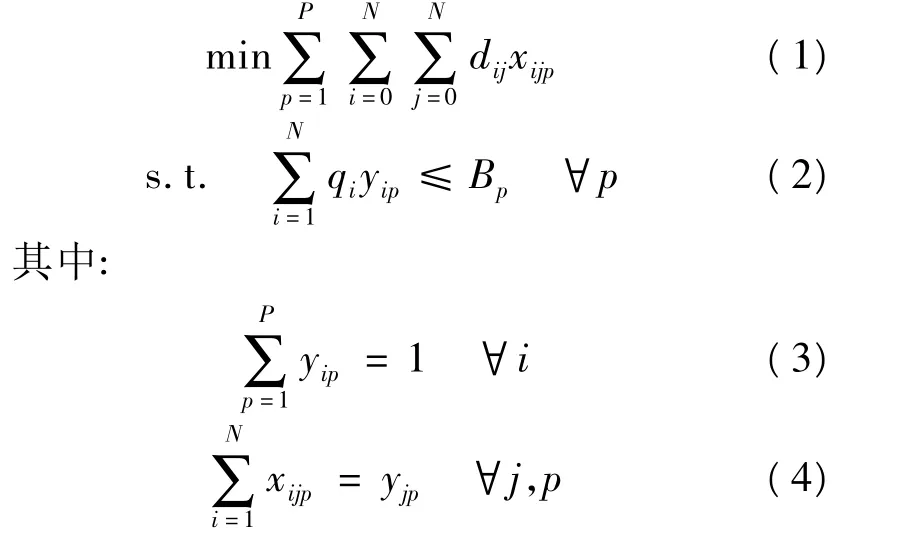
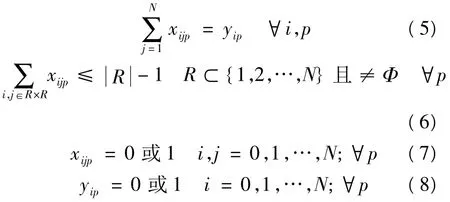
其中:式(1)为目标函数;式(2)为车辆载重能力约束;式(3)~式(5)保证了每个客户都被服务,且只有一辆车来完成任务;式(6)为消除子回路;式(7)和式(8)为变量取值约束。
2 免疫遗传算法的改进
基于信息熵的免疫遗传算法考虑了抗体浓度,并利用信息熵公式计算每个个体基因位置的信息熵大小,通过设定抗体浓度阈值来保证抗体的多样性。许多学者利用该算法进行了相关问题的研究,得到不错的结果。但该算法的缺陷是运行时间长,搜索速度较慢,且比较容易早熟收敛。为了克服这些缺点,笔者采用新的种群个体多样性保持策略,提出一种改进的免疫遗传算法[12]。
改进的免疫遗传算法的计算过程如下:
(1)初始化种群。系统初始化为一组随机解。
(2)计算所有个体的适应度,并选择出适应值最好的两个个体存入抗体记忆库。
(3)对种群进行遗传算法操作。该操作包括选择、交叉和变异等。
(4)更新抗体记忆库。如果抗体记忆库未满,选择最好的两个新个体更新补充记忆库;如果抗体记忆库已满,选择最好的两个新个体替换抗体记忆库中最差的两个个体。
(5)产生新种群。如果抗体记忆库未满,则抗体记忆库替换同等数量种群中最差个体组成新种群;如果抗体记忆库已满,优秀记忆抗体的数量越来越多,继续循环下去,抗体种群很容易达到局部最优,因此应该检查种群的多样性程度(第(6)步)。如果抗体多样性指数小于设定阈值,则随机生成新种群,然后让所有抗体记忆库的个体替换新种群中同样数量的最差个体,这样既大量保留了历代免疫遗传运算得到的优秀个体,又在传统优势个体中加入大批新生个体,新种群会在很大程度上避免局部最优解的出现;如果抗体多样性指数大于设定阈值,则按照记忆库未满时的方式产生新种群。
(6)检查所有个体的多样性程度,个体多样性程度用下式计算:
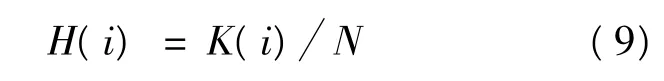
式中:H(i)为第i代种群的多样性指数;N为种群总个数;K(i)为第i代种群的一致性约简统计后的种群个数。具体计算方法为:在第i代种群中如果某个个体在种群中重复了多次,则该个体约简统计为1个,依此类推,种群中总共有K(i)个完全不同的个体。
从式(9)中可看出,所有个体都不相同时,H(i)最大为1。只有一种个体时,H(i)为1/N,达到最小。随着免疫遗传进化,优秀个体的数量重复率越来越高,H(i)也随着逐渐减小。这时设定H(i)的一个阈值,再对种群重新进行多样化操作。
(7)达到最大迭代次数则算法停止,最优秀的个体即为最优解;否则转回第(3)步。
改进的免疫遗传算法的最大特点是保留了免疫记忆机制,采用新的种群多样性程度的检测方法,减少了检测抗体之间亲和力的步骤。其计算量比传统的基于信息熵的免疫遗传算法大大减小。
3 能力约束VRP问题求解
根据上述改进的免疫遗传算法,给出了如图1所示的应用该算法解决有能力约束VRP问题的流程图。
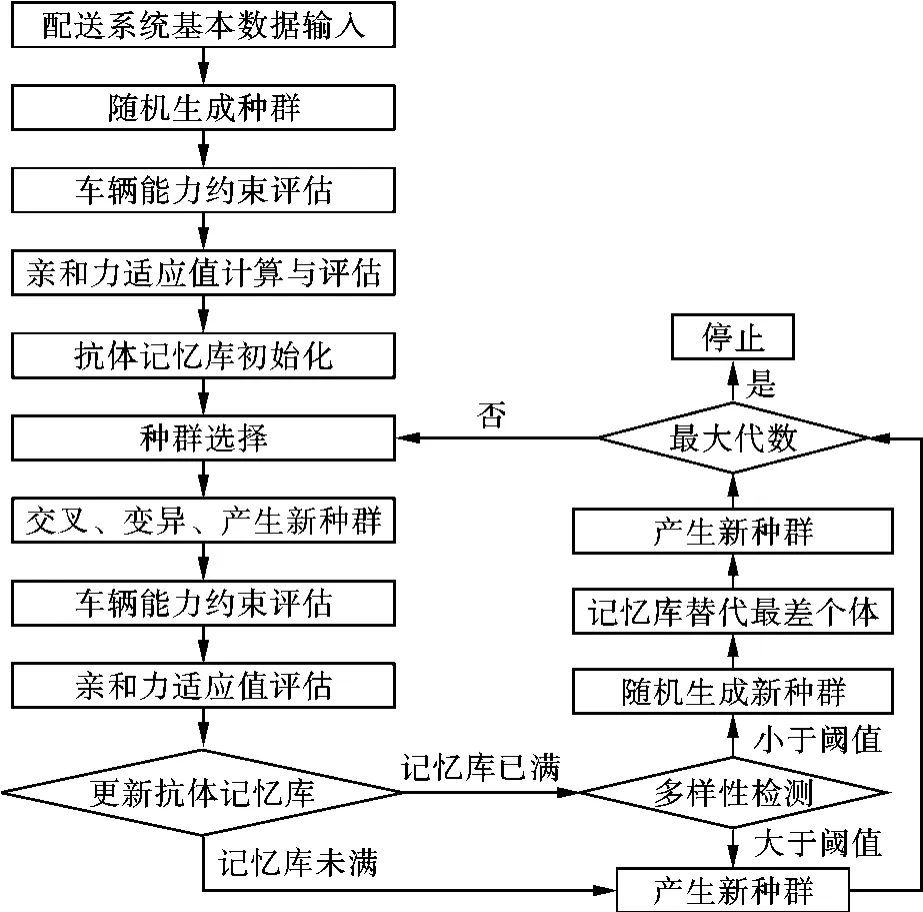
图1 改进免疫遗传算法求解VRP的算法流程图
(1)配送系统基本数据输入。基本数据包括配送系统客户与中心仓库的坐标或距离值、车辆载质量和客户运输需求量等,也包括改进免疫遗传算法的参数初始设置,如交叉率、变异率、记忆库容量参数、迭代次数和种群个数等。
(2)随机生成种群。针对VRP有不同的编码方式生成种群,笔者分别采取两种编码方案进行实验。第1种为客户随机排列方式,如有8个客户,则随机排列为1~8之间的整数;第2种为整数编码方式随机生成车辆分配方式,如两辆车8个客户,则整数随机排列为1~16之间的整数。每辆车最多可以服务的客户数就是总客户数。
(3)车辆能力约束评估。对随机生成的种群个体进行车辆能力的约束评估,对于第1种编码方式,依次判断排列车辆需求是否超出车辆载质量限制,如超出则换另外一辆车;不满足则为不可行解,通过惩罚的方式来尽快淘汰不可行个体。对于第2种编码,首先确定客户与路径的关系,然后判断客户需求是否满足,在车辆载重能力的约束下分配客户。如所有客户需求得到满足,则种群个体形成一个可行解;若不满足,则产生的个体是不可行解,通过惩罚的方式来尽快淘汰该个体。
(4)种群中抗体与抗原之间的亲和力适应值计算与评估。抗体与抗原之间的亲和力可以直接应用可行解的路径总和表示。由于有能力约束VRP是求总目标的最小值,为了程序设计方便,用总路径的倒数表示抗体与抗原之间的亲和力,即F=1/f,这样,程序的目标值就转化为求最大值问题,不可行解惩罚为最小实数。
(5)抗体记忆库初始化。抗体记忆库大小由种群个体的多少决定,一般设定为种群大小的20%~40%。记忆库每次从种群中选择最好的两个个体进行存储。抗体记忆库初始化是从初始化种群中选择抗体抗原亲和力适应值最好的两个个体进行存储。
(6)种群选择。按照抗原与抗体之间的亲和力选择进行遗传操作的个体一般采用轮盘赌的方式进行。
(7)交叉变异产生新种群。对选择出的个体采取循环交叉[13]的方法产生新的种群再以变异率为选择机制,对每个个体进行随机点变异,产生新的种群。
(8)车辆能力约束评估、亲和力适应值评估。对遗传操作后产生的种群再进行种群个体车辆能力的约束评估。对于不可行解,同样通过惩罚的方式将其淘汰。计算新种群的适应值和亲和力。
(9)更新抗体记忆库。如果抗体记忆库未满,更新补充记忆库;如果抗体记忆库已满,选择最好的两个新个体替换抗体记忆库中最差的两个个体。
(10)抗体记忆库未满,则抗体记忆库已有n个记忆抗体代替遗传操作后产生的新种群的前n个个体,从而组成新的种群。
(11)抗体记忆库已满时,首先,选择最好的两个新个体更新抗体记忆,然后进行多样性检测。如果抗体多样性指数小于设定阈值,则随机生成新种群,抗体记忆库和随机生成新种群重新组合成一个种群;如果抗体多样性指数大于设定阈值,则同步骤(10)。
(12)达到最大代数。如果达到设定的最大迭代次数则停止;否则,在新产生的种群中重新开始选择、遗传等操作。
4 实验研究
选用文献[5]中的配送系统,该配送系统中8个客户分别表示8个分仓库,另外有1个中心仓库。车辆限制为两辆,每辆车的载质量为8 t。表1中“0”代表中心仓库,其余表示中心仓库与客户之间的单位距离。
笔者分别应用两种编码方案进行实验研究。编码1为客户随机排列方式,编码2为车辆分配方式。
遗传算法的参数设定分别为:初始种群数量为50;交叉率pc=0.5;变异率pm=0.4;停止迭代次数为100。

表1 中心仓库、客户与客户之间的单位距离
客户运输需求量如表2所示。

表2 客户运输需求量
免疫遗传算法的参数设定分别为:初始种群数量为50;交叉率pc=0.5;变异率pm=0.4;抗体记忆库容量为RM=20;抗原抗体调节系数分别为a=0.7,b=0.2;停止迭代次数为100。
改进免疫遗传算法的参数设定分别为:初始种群个体为50;交叉率pc=0.5;变异率pm=0.4;抗体记忆库容量为RM=20;多样性阈值h=0.2;停止迭代次数为100。
实验最优解为67.5。路径排列次序为0—6—7—4—0;0—2—8—5—3—1—0。
图2为改进免疫遗传算法求解实验数据的一次结果。可以看出,到21代就达到了最优值,解的搜索也比较稳定。

图2 改进免疫遗传算法求解VRP适应值变化
表3列出了针对实例问题两种编码方案,采用3种不同算法进行50次随机试验的统计结果。从搜索成功率和最优解平均值可以看出,不管使用哪种编码方式,改进免疫遗传算法的计算效率都是最优的,特别是在采用第1种编码方案时,改进免疫遗传算法搜索最优解的成功率为100%。因此,笔者改进的免疫遗传算法在解决有能力约束VRP中是成功的。
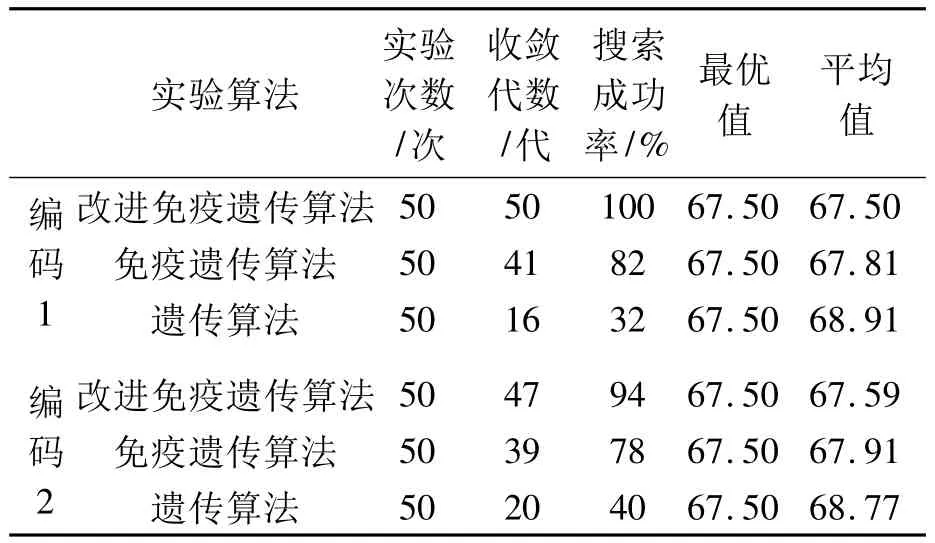
表3 几种算法结果比较
5 结论
人工免疫系统作为一种新兴算法,其应用领域需要进一步拓宽。选取VRP这个组合优化难题进行了实验研究,说明人工免疫系统算法的优势还是明显的。VRP随约束条件的拓展所产生的许多新问题也逐渐引起许多学者的重视,如大规模 VRP、有时间窗的 VRP[14]等,是下一步研究工作的重点。
[1]BODIN L,GOLDEN B,ASSAD A,et al.Routing and scheduling of vehicles and crew:the state of the art[J].Computers and Operations Researth,1983,10(2):63-212.
[2]KOLEN A W J,RINNOOY KAN A H G.Vehicle routing with time windows[J].Operations Research,1987,35(2):266-273.
[3]DANTZIG G B,RAMSER J H.The truck dispatching problem[J].Management Science,1959,4(6):80-91.
[4]CHENG R,GEN M.Fuzzy vehicle routing and scheduling problem using genetic algorithms[M].[S.l.]:Spinger-Verlag,1996:683-709.
[5]姜大立,杨西龙.车辆路径的遗传算法研究[J].系统工程理论与实践,1999(6):40-44.
[6]赵燕伟,彭典军.有能力约束车辆路径问题的量子进化算法[J].系统工程理论与实践,2009(2):159-166.
[7]DE CASTRO L N,VON ZUBEN F J.Artificial immune systems:basic theory and applications[R].Campinas:State University of Campinas,1999.
[8]焦李成,杜海峰.免疫优化计算、学习与识别[M].北京:科学出版社,2006:59-90.
[9]郎茂祥.配送车辆优化调度模型与算法[M].北京:电子工业出版社,2009:68-103.
[10]CHUN J,KIM M,JUN H.Shape optimization of electromagnetic devices using immune algorithm[J].IEEE Transactions on Magnetics,1997,33(2):1876-1879.
[11]梁勤欧.人工免疫系统与GIS空间分析应用[M].武汉:武汉大学出版社,2011:235-236.
[12]梁勤欧,周晓艳.基于免疫遗传算法的设备布局问题研究[J].武汉理工大学学报:信息与管理工程版,2011,33(4):643-646.
[13]OLIVER I M,SMITH D J,HOLLAND J R C.A study of permutation crossover operators on the traveling salesman problem[C]//Proceedings of the Second International Conference on Genetic Algorithm.New Jersey:[s.n.],1987:224-230.
[14]黄樟灿,蒋文霞,李书淦.有时间窗车辆路径问题的混合算法[J].武汉理工大学学报:信息与管理工程版,2008,30(1):48-51.

