一种轴扭转变形动态测量系统的设计及实现
丁珍红 吉小军 刘月华
上海交通大学,上海,200240
0 引言
轴扭转变形可以反映出轴的材料特性、负载特性及安全性等许多信息。在机械工程中,轴扭转变形的测量(包括静态和动态测量)是一项基础且极为关键的技术。静态测量主要对材料的扭转力学性能进行测试[1];动态测量主要测试能够间接表征旋转动力机械设备运行状况的扭矩、功率等信息,以对设备的动力特性、运行可靠性进行监测和故障诊断[2]。
实现轴扭转变形测量需要解决传感器、能量供给和信号传输三方面的问题。目前,国内外研制的传感器从原理上讲主要分为应变型、磁弹性型、转角型等[3]。其中,应变型使用最多,它采用在旋转轴表面贴应变片的传统方法,利用适当的电路取得信号,然后进行分析处理[4]。此种传感器因成本低、操作简便而被广泛使用在静态和低速旋转系统的扭转变形测量上,测量精度可达0.1%满量程,量程范围广,可满足多数应用需求,但该类扭矩传感器应用时需要妥善解决旋转条件下的可靠供电和信号传输问题。磁弹性型和转角型传感器因对制作、安装工艺要求高,目前在工业现场还很少获得应用。
在实际测量,尤其是动态实时测量过程中,一些特殊的条件,如工作环境恶劣(高温、高湿度、剧烈振动),安装空间有限,引线难度大,高转速等实际条件下,测量系统对传感器的性能会有更苛刻的要求[5]。光学测角法因具有非接触、高准确度和高灵敏度的特点而倍受人们的重视[6-7]。因此,笔者基于相位差测量原理提出并实现了一种扭转变形动态测量系统,可以解决恶劣条件下高速转轴的扭转变形的动态实时测量问题。
1 测量系统的工作原理与结构设计
长度为L的弹性轴在受到大小为N的扭矩作用时,轴将产生变形,任意两个横截面绕中心轴发生相对转动,从而产生一个扭转角θ:

式中,G为材料的剪切弹性模量;Ip为横截面对圆心的极惯性矩。
由式(1)可知,根据扭转角θ可以计算出扭矩N的值,但在实际应用中,由于扭转角非常小难于直接测量,一般都是通过一定的转换装置将其转化为脉冲信号的相位差来进行测量。目前常用的扭转式测量系统通过在轴上安装两个规格完全相同的齿轮和磁电式传感器实现[8-9]。扭矩作用时,两个与齿轮相对应的磁电式传感器将输出两路脉冲信号,通过测量这两路脉冲信号的相位差来实现扭转角的测量。这种系统结构复杂,体积与重量大,要求被测轴段有缩紧状结构,安装不便。笔者在测量轴上加工出色标带,利用反射式激光测头来得到包含转速与扭转角信息的脉冲信号,其结构原理如图1所示。

图1 测量原理示意图
在被测旋转轴上相隔一定间距的位置处平行粘贴、喷涂或加工反光与不反光的材料或结构,形成交替分布的反光与不反光的色标带,如图1所示。在与被测轴通过轴承相固连的套筒上A、B位置处安装2个反射式激光测头。当轴旋转且承受一定的扭矩载荷时,A、B处两个色标传感器(包括激光测头和色标带)的输出为频率相同但相位差一定的两路脉冲信号,脉冲信号的周期 T反映了轴的转速。在转速一定的情况下,色标条的数目决定了测量的动态特性。设色标条的数目为m,则脉冲信号的周期 T和转速n(r/min)的关系为

两路信号的相位差反映了扭矩载荷的大小,随着扭矩的增大,两路信号的相位差也增大,反之则变小,如图2所示。设 T1为两信号的相位差脉宽,由式(1)推导可以得到
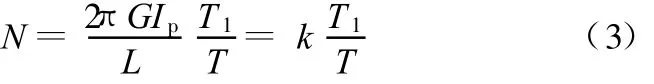
将式(3)代入式(1)得

由电工学原理可知
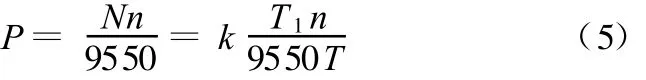
式中,k为由测量构件决定的比例系数;P为功率,kW。

图2 处理后的扭矩信号波形
由式(3)~式(5)可看出,只要测出脉冲信号的周期T和相位差脉宽T1,就可以得知一定扭矩载荷下扭转角的大小,通过测量扭转角便可得知轴变形并间接得到扭矩、功率的大小。
2 测量电路系统的方案设计
由上述测量原理可以看出,扭转角测量的关键在于对色标传感器输出的脉冲信号的周期和相位差脉宽的测量。本文以现场可编程门阵列(field-programmable gate array,FPGA)为核心,设计了专用的测量电路进行脉宽的测量和数据的存储及传输。
电路系统采取模块化的设计思想,包括电源电路、放大电路、精密整形电路、FPGA主控电路、FLASH存储电路、通信电路,其系统原理如图3所示。色标传感器将扭矩信号转化成电信号,经放大整形后送入精密整形电路得到两路同频方波,两路同频方波在FPGA内部经过异或运算得到表征相位差的脉冲信号,然后采用等精度测量技术测量其周期和脉宽,并将测量结果送到FLASH存储芯片AT45DB081中存储,需要时可将数据从存储器中读出,并经串口发送到上位机进行显示或后续处理。
FPGA采用硬件逻辑,具有功耗低、速度快、时钟频率高等特点,同时所有相关逻辑运算全部在芯片内部完成,从而简化了电路设计,并且高频信号全部在芯片内部,增强了系统的抗干扰能力[10]。系统中,周期和脉宽的测量主要通过FPGA中的计数器完成。采用等精度测量技术,可保证对任何频率的脉冲信号都能进行整周期记数,从而使因控制信号脉宽变化以及随机出现时间造成的误差,最多为标准频率信号的一个时钟周期。
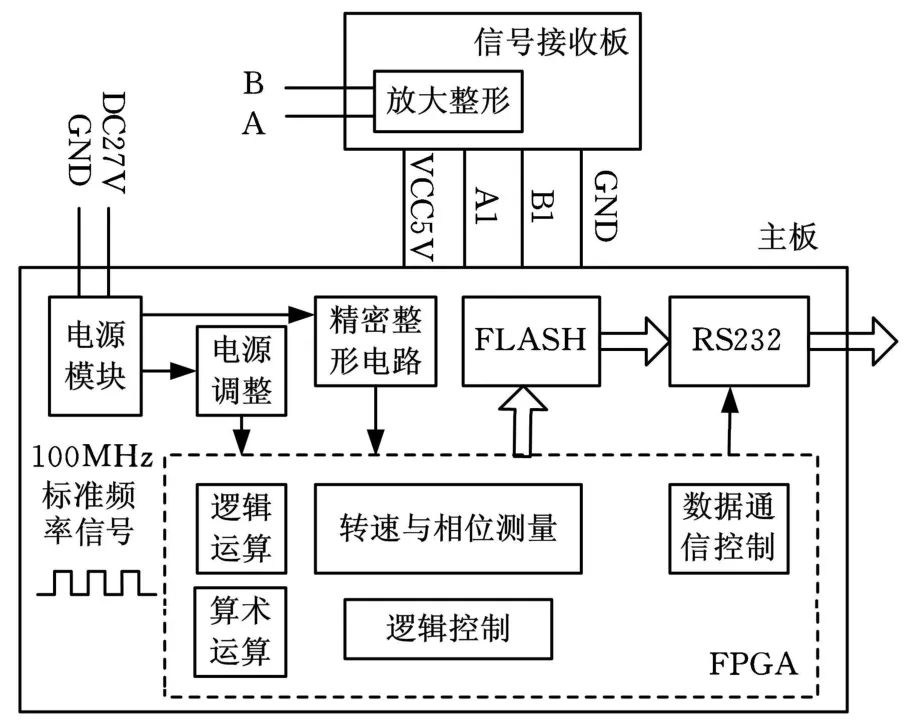
图3 系统原理框图
3 相位差的测定和仿真
式(4)给出了扭转角与相位差之间的换算公式,通过测量相位差便可进行扭转角的测量,如何对相位差进行准确测量是整个系统的关键。
前述两路信号的相位差与传感器安装的相对位置及旋转轴传递扭矩的大小有关。旋转轴在不受扭转载荷作用时,两路信号之间的相位差即初始相位差只与色标传感器的安装相对位置有关。空载情况下,使一端传感器固定,调整另一端传感器的位置。理论上讲,应保证两组光电接收装置输出波形的初相位差T0=0,但由于色标的加工误差、激光传感器的安装偏差等因素,故只能保证T0尽可能接近于0。当轴受扭转载荷作用时,两路信号(PA、PB)产生相位差,利用FPGA设计专门的鉴相模块(原理见图4)测量相位差。

图4 鉴相模块原理图
旋转轴在扭转过程中,输出的两路信号相位在理论上有两种情况:PA超前、PB超前。但由于振动、色标加工误差以及两个色标传感器的安装偏差等因素,故输出的两路信号之间还会出现相位不固定的情况。为了验证图4所示鉴相模块的适用性,对以上3种情况进行了仿真,如图5所示。
仿真结果表明,当PA、PB超前、滞后固定时,鉴相模块可以准确提取出PA、PB的相位差,而当PA、PB超前、滞后不固定时,鉴相模块无法准确获得两个信号间的相位差。为解决这一问题,本文中通过调整两端传感器的位置,改变PA、PB的初始相位差,使其理论值增大到π,以此保证轴旋转过程中,PA、PB超前、滞后固定,这样鉴相模块就能正确提取两信号间的相位差。
4 扭转变形动态实时测量的应用实现
根据上述扭转变形动态实时测量的工作原理和技术特征,拟在某一大型高精密高转速扭转角的应用系统中进行测试,该系统主要在恶劣条件下对高速转轴进行扭矩、功率的测量,由式(4)、式(5)可知,只要通过测量扭转角便可间接测量出旋转扭矩和旋转功率,在测试系统中,满载工况下的旋转速度控制为200r/min。
在测试系统(原理如图1所示)中,合金钢旋转轴的轴径D为120mm,综合考虑灵敏度及安装方便两个因素,反射式激光测头所在的A、B两点的轴向距离L取为600mm。考虑到测量的可靠性、加工与计算的方便,系统中采用30个色标条,即m=30。基于检测距离、响应时间、开关频率和延迟时间等因素的考虑,系统选用基恩士公司的激光测头FS-V30。
此外,电路控制系统中采用的晶体振荡器发出的信号频率为20MHz,利用FPGA内部的倍频模块PLL将标准时钟频率提高到100MHz,理论上的绝对测量误差只有10ns。
此相位差式扭转变形动态测量系统在某计量站进行了标定和验证,取得了满意的效果。表1所示为转速为200r/min、不同扭矩载荷工况下扭转角的测量数据,通过标准扭矩加载装置加载固定的扭矩载荷值,然后进行2~3min连续测量,对测量值取平均得到扭矩测量均值。表2为恒定扭矩(50N◦m)条件下的转速测量结果,同样,通过设置固定的转速,连续测量2~3min,对测量值取平均得到转速测量均值。测量过程中,进程、回程往返3次,分别对3次测量数据取平均得到一组进程数据、一组回程数据,用以验证重复性。图6所示为重复性测量效果。
从表1、表2和图 6可以看出,在2000N◦m的量程范围,对扭矩测量的精度小于0.5%满量程,完全能满足工程应用的需要。

表1 转速为200r/min工况下的相位差测量结果

表2 恒定扭矩(50N◦m)条件下的转速测量结果

图6 200r/min工况下扭转角测量的重复性
5 结语
本文以FPGA为核心设计并实现了一种轴扭转变形动态测量系统。该系统采用体积小、安装方便的色标传感器以及FPGA鉴相模块来测量相位差,并通过调整两路信号的初相位差,解决了实际测量中的相位差不固定的问题,从而实现了轴扭转变形的测定。由于是非接触式测量,因此大大提高了抗干扰能力和稳定性。最后通过仿真、现场标定和实际测试验证了该系统的性能。实验表明,在0~2000 N◦m量程范围内,扭矩和转速的测量精度均小于0.5%满量程,能有效地解决恶劣条件下高速转轴扭转角及转速的动态测量,从而解决动力传动中的扭矩及功率等测量问题。
[1]孙建军,杨南,方陆鹏.高精度大量程扭角测量仪的研制[J].实验室科学,2007,7(2):156-158.
[2]张晓玲,唐锡宽.转轴扭角及扭振测试技术研究[J].清华大学学报,1997,37(8):83-86.
[3]段国芳,苗岩松.国内扭矩测试方法综述[J].测试技术学报,1997,11(4):44-47.
[4]Turner J D.Development of a Rotating-shaft Torque Sensor for Automotive Applications[J].IEE Proceedings D,Control Theory and Applications,1988,135(5):334-338.
[5]张有,王家骐.扭转角动态实时监测系统[J].光学机械,1986(5):24-35.
[6]乔彦峰,王成龙,李向荣,等.莫尔条纹测量扭转变形角的方案研究[J].光学精密工程,2008,16(11):2133-2139.
[7]Pfister Pierre-Daniel,Perriard Yves.Torque Measurement Methods for Very High Speed Synchronous Motors[C]//Proceedings of the 2008 International Conference on Electrical Machines.Vilamoura,Portugal,2008:1-5.
[8]万德安,章阳宁.一种高精度扭矩测量系统的设计与实现[J].测控技术,2003,22(13):27-29.
[9]朱春梅,王朝霞,胡啸峰.扭矩测量系统的研究与设计[J].机械设计与制造,2009(5):30-32.
[10]赵威威,廖京川,余先伦,等.基于FPGA平均值原理相位差计的设计[J].电路设计,2009(6):18-20.

