非线性索单元等效多体动力学模型研究

杨志军 冯文贤 陈 新

广东工业大学，广州，510006

0 引言

缆索单元在工程领域有着广泛的应用，如桥梁拉索、起重拉索、运输索道等。缆索的运动方程为强非线性的偏微分方程，直接求解需要很大的计算量。很多文献用有限元法来求解绳索在外力作用下偏离平衡位置时的变形应力及动态响应[1－4]。应用有限元法时，必须有足够的约束条件，且不能发生刚体运动。绳索基本是柔性体，抗弯曲能力很小，在约束条件下绳索受外力时，沿绳索方向发生弹性变形，而沿法线方向运动却不受绳索的弹性限制，易出现大变形情况，必须考虑几何非线性。文献[3-4]从多体理论出发，提出计算绳索动力学的有限段模型，这种方法将绳索离散成为一系列铰接刚性绳段组成的多体系统，即用一系列具有不同几何物理参数的刚性绳段近似无限自由度的绳索，应用多体理论求解[5]。有限段方法的有效性在于它可以近似模拟绳索的轮廓形状，保持原有系统的质量分布特性，并可以采用多体系统中的刚体接触模型，求解起重和索道过程中绳索与驱动轮之间的接触关系。对于弹性索，李晓平等[6]在绳段间引入弹簧阻尼，并将多体运动力学和弹性力学相关理论结合起来，提出了采用铰接弹性段组成的多体模型，对弹性的处理效果类似于考虑了几何非线性的杆单元有限元法，可以处理绳索大范围的运动响应。对于预张紧桥梁拉索，文献[7]提出了非线性有限元模型，并在ABAQUS软件中进行了仿真。

客运索道中的拉索同样存在张力，由于工作过程中索道除了弹性变形，还需要做刚体运动，并与驱动轮进行接触，属于多体动力学范畴。ADAMS是多体动力学典型的仿真软件，但它不支持柔索单元。因此本文根据预张力非线性索单元模型，推导出绳索之间的连接力，将绳索离散成直径相等的圆柱小段，段之间用力连接。为了保证位移相容性，增加连接点扭矩和阻尼的联系，防止突变角位移的突变。将等效模型在ADAMS中进行了仿真，并通过计算得出了预张力钢丝绳的频率、振幅与张力的关系，验证了等效多体动力学模型的有效性。

胃切除术引起的体内神经-内分泌紊乱可导致继发性PEI[8]。胃切除患者体内碳酸氢盐和脂肪酶分泌显著降低。胃部分切除患者 PEI的发生率约70%，全胃切除患者PEI发生率高达100%[9]。

1 非线性索单元模型

设索单元是单向受力构件，随着应变的非线性增大，索力也呈非线性增大。在三维索单元计算中，坐标x、y、z和位移u、v、w 的变量表达式为[7]

式中，i、j均为节点编号。

应变公式为

结构运动方程为

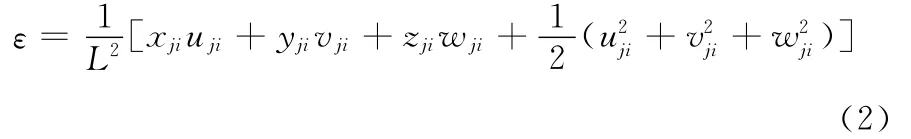
索单元的质量矩阵为

收获的薯块，运输前最好间隔一定时间使薯块表面干燥后、再及时装筐（一声），装筐时要轻拿轻放，避免薯皮大量擦伤或碰伤，不能及时运走的筐，应该用薯秧盖严压实，防止在阳光下暴晒而灼伤块茎。

式中，S为截面面积；E为弹性模量；F0为初始张力。

二十而南游江、淮，上会稽，探禹穴，闚九疑，浮于沅、湘；北涉汶、泗，讲业齐、鲁之都，观孔子之遗风，乡射邹、峄；戹困鄱、薛、彭城，过梁、楚以归。于是迁仕为郎中，奉使西征巴、蜀以南，南略邛、笮、昆明，还报命。

在总体坐标下，单元刚度阵为

通过引入弯曲刚度，建立的旋转自由度的受力联系，在线性（逐步加载）受载和运动范围内，可以保证位移的相容性。

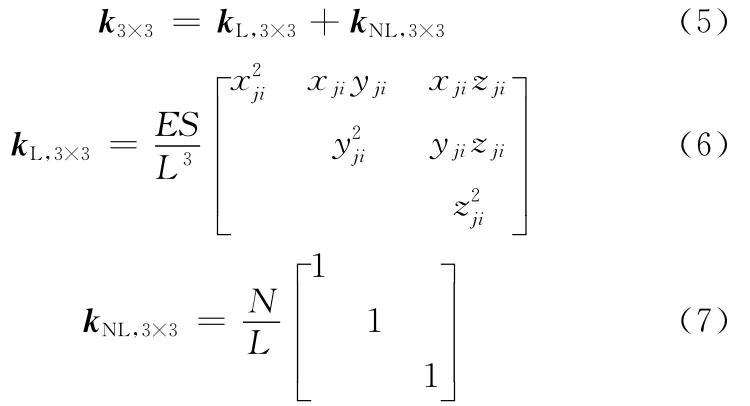
索单元的节点质量为

式中，L为索单元的长度。

法可依，有据可循。转移支付立法也要跟上，进一步科学界定专项转移支付和一般转移支付的内涵，真正发挥专项转移支付宏观调控的作用，同时发挥一般性转移支付弥补地方一般性公共支出的作用。推进转移支付的立法能够真正规范转移支付制度，也能真正在财政资金转移的过程中，将事权和支出责任下沉的渠道关闭。最后，还应及时探究并推进政府破产法，这是中央和地方财政关系重要的一环，地方财政发生重大危机，中央政府究竟怎么选择？如何把中央不救助原则落到实处？只有破除地方政府对中央政府的依赖性，才能够有效促进地方政府发债的合理性和规范性。■

式中，F为作用在结构上的外力；u为结构位移；M为总体刚度矩阵；K为总质量矩阵。

在不断变化的索道中求解该运动方程，得到节点的位移值。

组织相容性抗原在角膜上皮细胞、基质及内皮细胞均有表达。WHITSETT等[7]的研究结果表明，在年轻人的角膜中，这些抗原含量较年长人多。而PALAY等[8]的研究发现，来自年轻人的角膜植片在用于成年人的角膜移植术与发生排斥反应有很大的相关性，以此间接说明，移植排斥可能与供受体的年龄相关。然而在本次研究中，没有发现供受体年龄与角膜排斥概率有明显相关性。同时，也有一些文献认为供受体超过40岁，仍然是排斥发生的一个潜在危险因素[9]。

该单元模型已经被应用到有预紧力的荆州长江大桥斜拉桥的计算分析中，并证明了结果是可靠的[7]。在索道中，也存在有预紧力的钢丝绳，钢丝绳与绷轮、驱动轮、从动轮之间是通过摩擦进行传动的，属于多体动力学分析范畴。ADAMS是出色的多体动力学仿真软件，但它没有非线性索单元模型，因此需要根据非线性索单元模型进行等效多体动力学建模。

2 等效多体动力学模型

根据单元位移法，可以求出x、y、z三个方向的等效刚度。在ADAMS中，弹性连接是小位移假设，不适合于索单元等大变形问题。但ADAMS提供通用力连接，其中类轴衬选项可以模拟弹性连接，只需给出连接力的方程即可。索道离散刚体等效动力学模型如图1所示。

索的张力为

图1 预张力索多体动力学模型

根据非线性索单元的单元刚度矩阵，列出等效连接力如下：

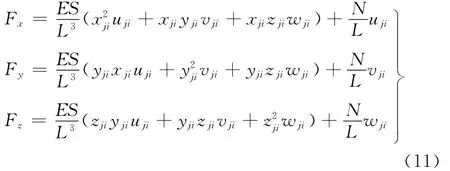
离散后的钢丝绳每一小段有12个自由度，总自由度数为12n（n为离散单元数）。与有限元法不同，单元的力连接并不减少自由度方程数，只是建立了相连节点的受力平衡关系，并不能保证位移（特别是角位移）的相容性。因此，需要增加连接点转矩T和扭转刚度KT与阻尼CT的联系：

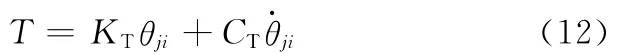
式中，θji为单元的j节点与另一个单元i节点的夹角为转动速度。

防止突变角位移的突变。

其中，单元刚度矩阵的子矩阵k3×3分别由线性和非线性矩阵项组成：

3 非线性索道张力下的振动分析

为了验证预张紧钢丝绳等效多体动力学模型的有效性，建立了长为20m、半径为8mm，且两端铰接的一段钢丝绳模型。每50mm离散成一段刚体，共有400个单元。所用材料为钢，钢丝绳拉伸时的弹性模量为110GPa。对不同张力下的运动情况进行分析，线性加载时间为1s，一共分析了5s内的受力情况（图2中示出了0～2.5s的情况）和运动情况（图3中示出了0～2.5s的情况），振动频率由2～5s内稳态响应曲线经过傅里叶变换后的频谱分析得到（图3b）。张力取不同的值，得到的分析结果列于表1。

FastEthernet0/0 128.1 128 19 FWD 0 4096 cc00.1ca0.0001 128.1

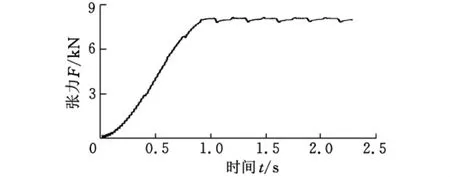
图2 张力为8kN下的拉力曲线

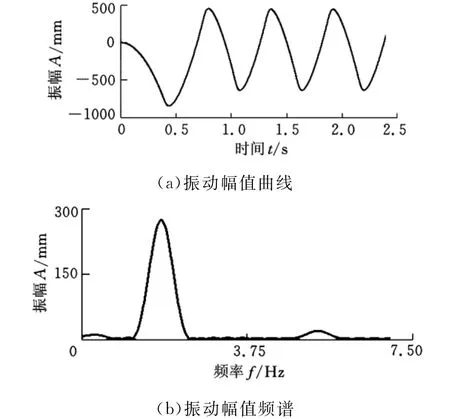
图3 张力为8kN下的振动幅值曲线和频谱

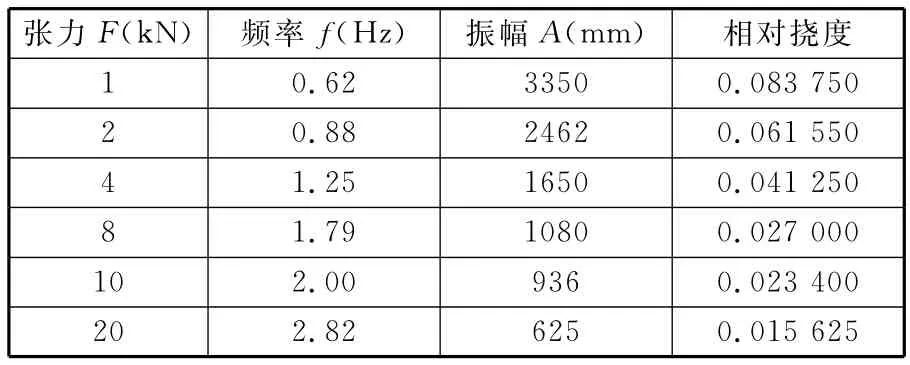
表1 钢丝绳在不同张力下的振动情况

3.1 频率与钢丝绳张力的关系

从表1数据中，绘出频率与张力的关系，并通过曲线拟合，得出拟合曲线，如图4所示。可以看到，半径为8mm、长为20m钢丝绳的振动频率与张力呈指数函数关系f＝0.6201F0.5072，与理论解y＝ax0.5（a为系数）相符。

综上所述，格鲁吉亚首都第比利斯爆发重大群体性突发事件的原因相当复杂，绝非单一原因。需要指出的是，许多人称与群体性事件都“是自发的”，“并没有什么事先的预谋。”[11](P132)事实并不像有人猜测的那样：“青年人是受比较年长的组织者操纵”。[4](P101)即使时隔45年之后，曾经自发参与当年游行示威的人在2001年春天俄罗斯的电视转播中还这样解释自己的行为：“我们不能不到广场去，大家都在那里！”[14]

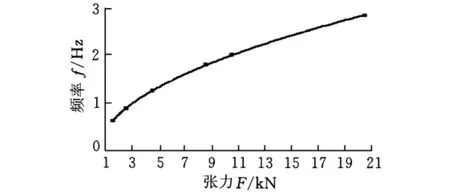
图4 频率与张力的关系（f＝0.6201F0.5072）

3.2 振幅与钢丝绳张力的关系

同样，绘出振幅与张力的关系，并通过曲线拟合，得出拟合曲线如图5所示。可以看到，半径为8mm，长为20m钢丝绳的振幅与张力呈指数函数关系A＝3513.1F－0.5697，符合实际情况。

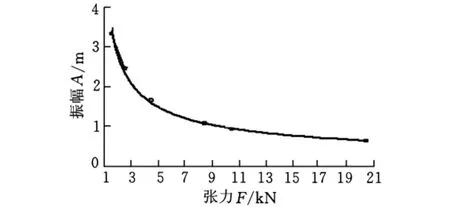
图5 振幅与张力的关系（A＝3513.1x－0.569 77）

将创建预张力索道等效动力学模型方法编写成程序，并生成ADAMS软件可执行的命令文件，再运用到本文所述的非线性索道单元等效动力学模型应用与试验索道多体动力学分析中，得到的动力学模型如图6所示。

图6 试验索道整体动力学模型

4 结语

本文建立了非线性索单元的多体动力学等效模型，为索道整体的多体动力学仿真提供了依据。在ADAMS中建立了20m预张力钢丝绳模型，通过多体动力学仿真，得到了不同张力下的钢丝绳振动频率和振幅，并分析了振动频率、振幅与张力的关系。本文结论为索道系统的多刚体动力学仿真提供了依据，也为ADAMS对带传动、链传动等非线性单元的仿真提供了参考。

[1]丁虎.轴向运动梁横向非线性振动建模、分析和仿真[D].上海：上海大学，2008.

[2]王连华.斜拉索的非线性动力学分析[D].长沙：湖南大学，2001.

[3]Kammen J W，Huston R L.Modeling of Variable Length Towed and Tethered Cable System [J].Journal of Guidance，Control，and Dynamics，1999，22（4）：602-608.

[4]Huston R L，Kammen J W.Validation of Finite Segment Cable Models[J].Computers and Structures，1982，15（6）：653－660.

[5]休斯顿，刘又午.多体系统动力学[M].天津：天津大学出版社，1991.

[6]李晓平，王树新，何曼丽.海洋缆索的动力学仿真研究[J].海洋技术，2005，24（1）：52-57.

[7]庄茁，由小川，廖剑晖，等.基于ABAQUS的有限元分析和应用[M].北京：清华大学出版社，2009.