饱和土二维固结试验在离心力场条件下的适用性分析

张莎莎，谢永利，刘保健

(长安大学公路学院，陕西 西安710064)

0 引言

随着城镇建设事业及交通行业的迅猛发展，工程用地已是寸土寸金，如何合理治理饱和土的工程病害早已成为工程治理中的重要课题之一.目前，离心模型试验技术是各类土工物理模型试验中相似性能最好的试验方法［1-3］，且已探索出了很多有益的试验经验［4］.然而，大量离心模型试验过程中，由于试验条件限制，通常认为其进行的都是一维单面排水固结试验［5］，对于在有侧限情况下的二维固结排水模拟试验基本未见到相关的报道.

实际工程中，地基的侧向排水会加速超静水压力的消散，对其固结沉降速率有较大影响.为了探索更接近于实际工况的土体固结特性及其在二维排水条件下饱和土的离心模型试验特点，研究饱和土样在离心力场下的适用条件，笔者针对典型区域饱和土样海相土、湖相土及河相土分别进行了在离心力场条件下的适用性条件分析，为今后采用离心模型试验研究土体的二维固结特性进行探索性研究.

1 典型区域土样的基本工程性质

为了使试验结果更具有代表性，所取试样分别为宁波海相土、洞庭湖地区湖相土及渭河二级阶地湿软黄土，对试验土样进行了基本工程性质的测试，所测项目均做了3组平行试验.土样的基本工程性质列于表1.

表1 土样的基本工程性质Tab.1 Physico-mechanical properties of soil samples

2 离心模型试验

2.1 试验装置设计

目前，研究土体固结压缩特性最基本的方法是室内侧限固结压缩试验，为了与常规固结试验结果进行对比分析，对离心机所配备的模型箱进行了加工改装.由于常规固结试验的容器是圆柱形，本次试验亦给模型箱中加工相似形状的有机玻璃筒［6］，其径高比以标准常规固结试验环刀的径高比为依据和参考，并依据离心试验模型箱的长宽高(700 mm×360 mm×500 mm)的限制来确定.试筒装置结构如图1所示.试筒装置与离心机自配模型箱之间的连接支架如图2所示.

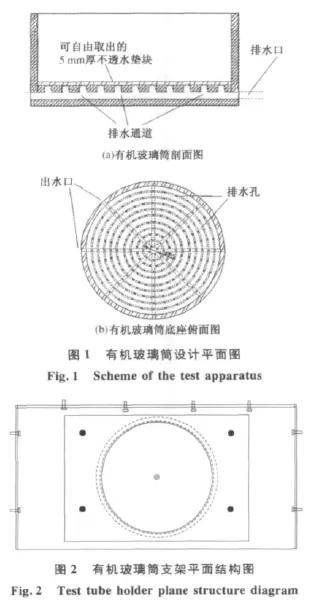
有机玻璃试筒底部有排水通道，双面排水试验时，可以取出有机玻璃底板;单面排水试验时，可以将有机玻璃底板放入筒内，并密封.设计两种试筒，一种试筒侧面为实体有机玻璃，一种试筒侧面的有机玻璃均匀密布排水小孔.

在使用有机玻璃试筒来模拟土体固结试验过程时，由于水自身重力的原因，土体上表面、底面和侧向固结排出的水可以直接排到外围的模型箱中，对固结试验过程的干扰减小.为使试筒在离心机转动过程中不产生侧面变形，随即也设计了有机玻璃试筒的卡箍装置及其在模型箱中的固定装置(图2).固定试筒装置的支架三面有定位螺丝，可有效调节钢支架在离心机自配模型箱中的位置.在钢支架中心安置试筒的四周也有4个定位螺丝，可直接帮助调节试筒处于模型箱的中心.安装测量仪器的支架为航空铝合金材质，在安装时选择了小跨度，试验证实在100 g的情况下其变形挠度非常微小可以忽略不计.

试验采用的离心机型号是TLJ-3型土工离心机，其有效半径为2.0 mg.土体固结沉降变形测量仪器为ILD1300-100型非接触式激光位移传感器，该传感器可直接对土样沉降变形进行测量，对土样无干扰.土压传感器和孔隙水压力传感器均为微型传感器，它们的型号分别为BW-0.6型和BWL-0.4型.

2.2 试验方案

为了减少其他因素的干扰，试验模型土样采用均质土体.因此，对土样进行了晾晒、过2 mm筛、浸水饱和的处理.浸水饱和时间不少于10 d，经检测土样的饱和度基本达到99%以上.

模拟二维固结排水的离心模型试验圆柱筒的周边及底层布设了滤纸，以使在试验过程中只有水被排出试筒外.模型试验安排如表2所示.

为了与二维固结试验进行对比分析，亦做了两组一维单面排水固结离心模型试验，方案见表3.

在试验过程中，部分试验加测了土压力及孔隙水压力，为了避免埋设于土中的传感器对土体的固结变形过程产生影响，在该种情况下的固结试验结束后，再做相应的只架设非接触式激光位移传感器来测试土体的变形.

表2 饱和土样二维固结离心模型试验Tab.2 Schemes of centrifugal modeling tests for two-dimensional consolidation

表3 饱和土样一维固结离心模型试验Tab.3 Schemes of centrifugal modeling tests for one-dimensional consolidation

2.3 离心模型试验结果及分析

2.3.1 固结沉降与时间的关系

在离心模型试验过程中，由于饱和软土的完全固结是个缓慢的过程［7］，为了节约试验时间，通过对测试仪器传输到电脑中的数据进行实时监控，然后通过数据模拟软件OriginPro7.5来对试验时间进行控制［7-8］，在固结沉降量基本超过70%的总沉降量时，试验停止.二维离心模型试验过程中，各土样固结沉降和试验时间的关系曲线如图3～6所示.

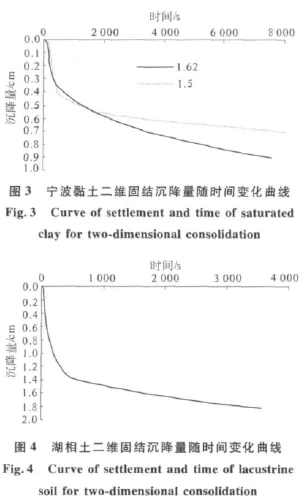
从图3～5可知，3种类型饱和土的沉降量随时间变化的规律基本相似.由于宁波饱和黏土的固结系数较小，其固结沉降主要分为斜率较陡的线性快速固结和斜率较缓的线性缓慢固结两个主要固结阶段，其中缓慢固结沉降量所占总沉降量的比例是比较大的，基本大于65%.洞庭湖地区饱和湖相土的固结系数相对较大，固结沉降随时间变化主要可以分为线性快速固结和缓慢固结，其线性快速固结阶段所完成的沉降量基本占到总沉降量的70%以上.饱和黄土快速固结和缓慢固结之间的衔接非常缓和，线性增长并不明显，整个固结阶段呈现曲线型增长.

从图3、图5可知，当初始孔隙比不一样时，同种类型饱和土的前期固结阶段沉降量随时间变化的趋势是基本重合的，沉降量增长速率基本一致.进入缓慢固结阶段以后，初始孔隙比较大的饱和土沉降量增长速率逐渐增大，与初始孔隙比较小的沉降量增长趋势分离.

为了与饱和土的离心模型二维固结试验进行对比分析，同时进行了离心模型一维固结试验.试验过程中，固结沉降量与时间的关系曲线如图6所示.

从图3、图5和图6中可以看出，离心模型一维固结沉降速率明显小于二维固结沉降速率.两种土的离心模型一维固结沉降量随时间变化规律基本是相似的，分为线性快速固结和曲线形缓慢固结两个主要阶段.两种土的一维固结试验中，曲线形缓慢固结沉降量占总沉降量的比例都很大.

利用模拟软件OriginPro7.5对试验所得固结沉降量随时间的变化曲线进行指数关系拟合，可以得到式(1)，其中拟合参数如表4所示.

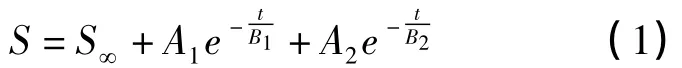
式中：S为土体的沉降量;S∞为土体最终沉降量;t为试验时间;Ai和Bi为试验常数，与试验条件和土性有关.

表4 二维固结拟和参数Tab.4 Fitting parameters

由于拟合曲线R2≥0.99，即式(1)对曲线可进行合理预测.对应的实际结果应乘以相应的n.

2.3.2 离心模型试验中土体的固结特性

为了研究离心模型二维固结试验过程中土体的固结特性随时间的变化规律，对土体的土压、孔压和试验结束后的含水率进行了测定，土压及孔隙水压力传感器设于土柱体底部，结果如图7～9所示.

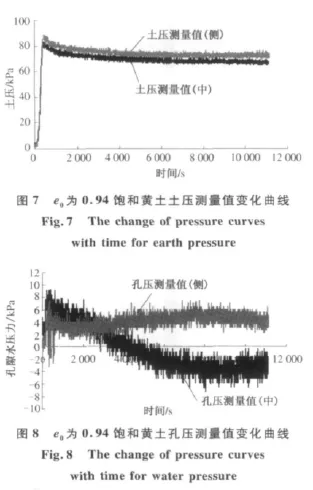
从图7的土压传感器测量值随离心时间的变化曲线中可以看出，两种土压力传感器的测量值都是随着离心时间的增大，先增大再减小而后趋于稳定.在试验初期离心加速度的增大过程即是土层厚度的增大过程，这一过程中土压力测量值就会随着土层厚度的增加而增大;加速度稳定以后，土层厚度不再增大，土体固结沉降变得明显，此时孔隙水压力的消散过程亦呈现比较明显的态势，很多水都被排出在试筒之外，土加水的总量减小，从而导致整个土体的压力减小，但是随着土体固结的逐渐稳定，水的消散量也减小，土压传感器的测量值趋于稳定.位于土体底部中心区域的土压测量值稍低于周围的土压测量值，可以看出离心模型试验过程中离心加速度分布并不完全均匀的特性.

从图8可以看出，孔隙水压力随着离心加速度的增大也有一定的起伏变化.但是，随着离心加速度稳定后，孔隙水压力传感器的测量值就开始迅速减小.孔压测量值(侧)在减小的过程中稍有起伏，但是随着时间的推移孔压传感器的测量值逐渐趋于零.孔压测量(中)值则是随着离心时间的增大而迅速减小，甚至出现负孔压，而后有趋向“零”孔压的趋势，即回到初始测量值.产生负孔压主要是因为在离心力作用下，由于是二维排水固结，在某些局部区域的土体还未来得及变形，但是水早已排出，因此产生了局部意义上的真空，孔压随即出现负值，但从长期来看，孔压有慢慢恢复到“零”的趋势，即初始值.

图9 含水率在土柱体的分布Fig.9 Profiles of water content

图9为离心试验结束后土柱体中含水率的分布曲线.从图中可以看出，两种土柱体中，底层含水率都较小，顶层含水率较大，土柱体中部的含水率随着土体的渗透系数不同呈现一定的差异.渗透系数较小(即固结系数较小)的海相土含水率分布更接近于理论.

3 结论

(1)固结系数较小的宁波饱和黏土，其离心模型二维固结沉降主要分为斜率较陡的线性快速固结和斜率较缓的线性缓慢固结两个主要固结阶段，其中缓慢固结沉降量所占总沉降量的比例较大，基本大于65%.

(2)固结系数相对较大的洞庭湖地区饱和湖相土的离心模型二维固结沉降随时间变化主要可以分为线性快速固结和缓慢固结，其线性快速固结阶段所完成的沉降量基本占到总沉降量的70%以上.

(3)饱和黄土离心模型二维固结试验中的快速固结和缓慢固结之间衔接非常缓和，线性增长并不明显，整个固结阶段呈现曲线型增长.

(4)在离心模型试验中，初始孔隙比不同的同种类型饱和土，其前期二维固结阶段沉降量随时间变化的趋势是基本重合的，沉降量增长速率基本一致.进入缓慢固结阶段以后，初始孔隙比较大的饱和土沉降量增长速率逐渐增大，与初始孔隙比较小的沉降量增长趋势分离.

(5)在离心模型试验中，土柱体的二维固结特性与理论基本相似，固结系数较小的宁波海相土试验结果更接近于理论，离心模型试验具有饱和土样二维固结模拟的基础。

［1］钱家欢，殷宗泽.土工原理与计算［M］.北京：中国水利水电出版社，1996.

［2］包承纲.我国离心模拟试验技术的现状和展望［J］.岩土工程学报，1991，13(6)：92-97.

［3］包承纲，饶锡保.土工离心模型的试验原理［J］.长江科学院院报，1998，15(2)：2-7.

［4］谢永利，潘秋元，曾国熙.应用离心模型试验研究软基变形性状［J］.岩土工程学报，1995，17(4)：45-50.

［5］REZZOUG A，KÖNIG D，TRIANTAFYLLIDIS T.Scaling laws for centrifuge modeling of capillary rise in sandy soils［J］.Journal of Geotechnlcal and Geoenvironmental Engineerling，2004，130(6)：615-620.

［6］POULOSE A，NAIR S R，SINGH D N.Centrifuge modeling of molsture migratlon in silty soils［J］.Journal of Geotechnical and Geoenvironmental Engineering，2000，26(8)：748-752.

［7］杨坪，唐益群，王建秀，等.基于大变形的冲填土自重固结分析及离心模型试验［J］.岩石力学与工程学报，2007，26(6)：1212-1219.

［8］张莎莎.基于离心模型试验的饱和土固结理论研究［D］.西安：长安大学公路学院，2011.