多尺度的灰值形态学在图像边缘检测中的应用

师惠萍，程耀瑜，刘永林，王诗琴

（中北大学信息与通信工程学院，山西太原 030051）

0 引言

图像边缘是指图像局部强度变化最显著的部分，往往是由图像中景物的物理特性发生变化而引起的。边缘检测就是检测图像局部特征值（如灰度等）不连续或变化较为剧烈的像素点，把这些点连接起来就形成物体的边缘。检测图像边缘信息的常用方法是判断某像素点是否为边缘点［1］。传统的边缘检测方法是利用边缘邻近的一阶导数或二阶导数变化规律来考察图像的每个像素的某个邻域内灰度的变化。典型的边缘检测算子有Robert算子、Sobel算子和Canny算子等［2］。这种方法对噪声比较敏感，常常在检测边缘的同时又加强了噪声。

近年来，数学形态学方法在图像分析中起着越来越重要的作用。它的基本思想是用具有一定形态的结构元素去量度、提取图像中对应的形状，以达到对图像分析和目标识别的目的［3］。形态学运算是物体形状集合与结构元素之间的相互作用，它对边缘方向不敏感，并能在很大程度上抑制噪声和探测真正的边缘。因此，将数学形态学应用于边缘检测，既能有效地滤除噪声，又能保留图像中原有的细节信息，具有较好的边缘检测效果［4］。初期的形态学图像处理，采用单一结构元素的比较多，这不太利于信息几何特征的保持，随着应用的不断深入，人们逐渐探索出采用多结构元素进行图像处理的方法［5，6］。

本文采用改进的灰值形态学边缘检测算子，利用大小不同的结构元素提取图像边缘特征，大尺寸的结构元素去除噪声能力强，但所检测的边缘较粗;小尺寸的结构元素去噪声能力弱，但能检测到好的边缘细节，因此将各种不同尺寸下的边缘图像结合起来就可提取出较理想的边缘。

1 灰值形态学

灰值形态学是数学形态学的一种，由二值形态学理论推广而来。它可以应用于各种灰度图像和彩色图像，其基本运算主要为灰度腐蚀、灰度膨胀、灰度开启和闭合四种。设f（x，y）是输入图像，b（x，y）是结构元素，且都定义在R2或Z2上，Df和Db分别是函数f（x，y）和b（x，y）的定义域。

1.1 灰度膨胀

灰度膨胀记为f⊕b，其定义如公式（1）所示:

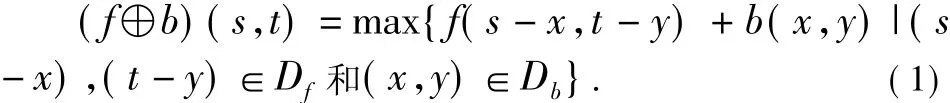
它是一个扩张的过程，能使目标扩张，孔洞收缩。该运算是在由结构元素确定的领域中选取的f⊕b最大值。如果结构元素的值都为正，则输出图像的灰度值会比输入图像高，与灰度值高的像素相邻的暗细节的灰度值会提高，输出图像就会表现为暗细节被削弱或去除，亮区域的范围得到膨胀。根据膨胀运算的特性，可用于暗细节的消除，亮区域边缘的增强。

1.2 灰度腐蚀

灰度腐蚀记为fΘb，其定义如公式（2）所示:

它是一个收缩的过程，能使目标收缩，孔洞扩张。该运算是在由结构元素确定的领域中选取fΘb的最小值。如果结构元素的值都为正，则输出图像的灰度值会比输入图像低。在输入图像中亮细节的尺寸比结构元素小的情况下，其影响会被减弱，减弱的程度取决于这些亮细节周围的灰度值和结构元素的形状和幅值。输出图像外观表现为边缘部位较亮细节的灰度值会降低，较亮区域边缘会收缩。

1.3 灰度开启

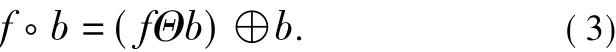
该运算是先对图像腐蚀再膨胀。该运算可以平滑图像轮廓，去除图像中的细小突出。

1.4 灰度闭合

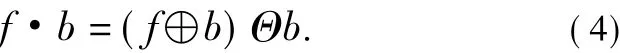
该运算是先对图像膨胀再腐蚀。该运算可以平滑图像轮廓，填平小沟，弥合孔洞和裂缝。

1.5 灰值形态学梯度

对于灰度图像，由于图像中边缘附近的灰度分布具有较大的梯度，我们可以利用图像的形态学梯度方法来检测图像的边缘。将灰度膨胀和灰度腐蚀运算相结合可用于计算灰度图像的形态学梯度。设灰度图像的形态学梯度用g表示，则形态学梯度算子可表示为:1.6 灰值形态学图像边缘检测基本思想

用灰值形态学进行图像边缘检测的基本思想是把结构元素作为“探针”收集图像信息。当探针在图像中不断移动时，便可完成对图像的处理［7］。运用各种基本运算的复合算法，构造边缘检测算子，从而了解图像的边缘结构特征。其基本过程如图1所示。

图1 灰值形态边缘检测过程

在上述过程中，结构元素的特点和边缘检测复合运算方式决定了图像处理结果。其中结构元素的形状、尺寸决定处理结果的效果和精度，复合运算方式反映了处理结果与原图像的关系。

2 多尺度灰值形态学在图像边缘检测中的应用

2.1 结构元素对边缘检测的影响

结构元素是数学形态学的基本要素，结构元素的不同直接决定分析和处理图像的几何信息的不同，同时也决定了运算使用数据量的不同。结构元素的形状和尺寸会影响图像边缘检测的效果:水平方向的结构元素对竖直方向的边缘比较敏感;竖直方向的结构元素对水平方向的边缘比较敏感;小尺寸的结构元素去噪声能力弱，但能检测到边缘细节;大尺寸的结构元素去噪声能力强，但检测的边缘较粗［8］。本文使用多尺度灰值形态学检测图像的边缘，结构元素选择方形结构，尺度分别为1×1，2×2，3×3，4×4四种结构元素。

2.2 多尺度形态学边缘检测算法

本文采用改进的形态学梯度检测算子，设Bi（0≤i≤n）

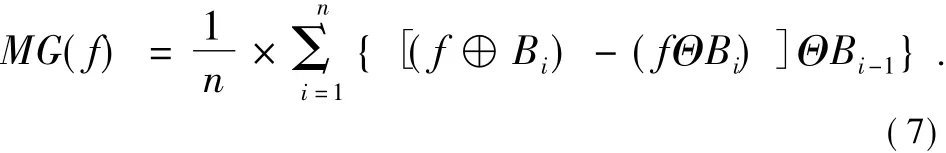
边缘检测算法具体步骤如下:先分别用尺度为1×1，2×2，3×3，4×4的结构元素检测出原始图像的边缘信息，然后用多尺度定义合成算法得到新的边缘图像。

2.3 传统算子比较结果

本文采用 Visual C++ 编程实现算法［9，10］，并将改进算子与传统边缘检测算子的检测结果进行比较。传统算子选取Robert算子、Sobel算子和Canny算子。实验中采用的灰度图像如图2所示，传统算子与本文算子检测结果如图3所示，由各图检测结果可以看出:Sobel和Robert算子在蚂蚁的四肢和腹部部分有漏检现象，检测的边缘连续性较差;Canny算子对蚂蚁检测边缘较完整，但是由于对噪声比较敏感，在蚂蚁的上方和下方产生了许多假边缘，影响了算法执行的效率;图3（d）是本文算子检测出的图像，该算子检测出较完整的边缘且没有假边缘产生。为一组正方形的结构元素，单尺度形态学检测算子定义为:

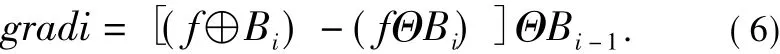
则多尺度定义为:

图2 实验源图像

图3 传统算子与文中算子比较结果

3 结论

通过与传统边缘检测算子的比较可以看出，将多尺度灰值形态学方法应用在图像边缘检测具有重要的理论价值和应用价值，该方法是可行的。在实际应用中，选取不同的结构元素，结合多尺度或多结构元素的特性，构造优良的边缘检测算子，可以较好地解决边缘检测精度与抗噪声性能的协调问题，取得较好的边缘检测结果。

［1］李依令.基于多尺度多结构元素的数学形态学边缘检测［J］.科学技术与工程，2006，10（6）:1417-1419.

［2］黄剑玲，邹辉.一种基于形态学的多结构元素多尺度图像边缘检测方法［J］.微电子学与计算机，2009，8（26）:76-79.

［3］章毓晋.图像处理和分析教程［M］.北京:人民邮电出版社，2009:286-306.

［4］夏平，刘馨琼，向学军，等.基于形态学多结构基元的含噪图像边缘检测［J］.计算机仿真，2010，7（27）:206-209.

［5］KANG Huai-qi，SHI Cai-cheng，ZHAO Bao-jun，et al.A Method of Edge Detection Based on Emended Mathematical Morphology［J］.Optical Technique，2006，32（4）:634-638.

［6］HOU Zhi-qiang，HAN Chong-zhao，ZHENG Lin，et al.Denoising Algorithm of Remote Sensing Image Based on Lacal Multiple Morphological Structure Elements［J］.Chinese Journal of Radio Science，2004，19（4）:427-430.

［7］陈宁，刘全玺.基于数学形态学的CT图像边缘检测方法［J］.天津科技大学学报，2006，3（21）:66-67.

［8］黄海龙，王宏，郭璠，等.一种基于数学形态学的多形状多尺度边缘检测算法［J］.东北大学学报（自然科学版），2010，10（31）:1483-1486.

［9］王占全，徐慧.精通Visual C++数字图像处理技术与工程案例［M］.北京:人民邮电出版社，2009:54-89.

［10］谢凤英，赵丹培.Visual C++数字图像处理［M］.北京:电子工业出版社，2008:397-411.