JPEG算法的研究及其在医学图像中的应用

阎 冲，孙运强，姚爱琴

（中北大学信息与通信工程学院，山西太原 030051）

0 引言

PACS（Picture Archiving and Communication Systems，医学影像存档与通信系统）是旨在全面解决医学图像获取、显示、存储、传输和管理的综合系统［2］。医学图像的数量增长速度非常快，为了减少存储空间，对其进行压缩是必须的［3］。医学图像自身的特殊性对压缩技术提出了更高的要求，图像压缩所解决的问题是尽量减少表示数字图像时所需要的数据量。减少数据量的基本原理是减少其中的冗余数据［4］。而JPEG算法研究及其在医学图像中的应用有着重要的意义，这就为PACS系统和远程医疗系统中的图像便捷存储和快速传输提供了有效的解决方法。

1 JPEG压缩编码算法的研究及实现

JPEG的目标是开发一种用于连续色调图像压缩的方法，这种方法必须满足以下4点要求:（1）应用当前的先进图像压缩技术。在保证压缩率的同时，图像质量要好，即失真程度要在一定的范围之内。（2）适用于所有的连续色调图像，不应对图像的尺寸、彩色空间和像素纵横比等特性进行限制，也不应对图像的场（如复杂度、彩色范围或统计特性等）有任何要求。（3）具有适中的计算复杂度，从而使得压缩算法既可以用软件实现，也可以用硬件实现，并具有较好的性能。（4）具有4种操作模式:顺序编码、累进编码、无失真编码、层次编码［5］。

JPEG压缩编码算法的主要计算步骤如下:

（1）颜色模式转换及采样

RGB色彩系统是我们最常用的表示颜色的方式。JPEG采用的是YCbCr色彩系统。想要用JPEG基本压缩法处理全彩色图像，得先把RGB颜色模式图像数据，转换为YCbCr颜色模式的数据。

（2）DCT变换

变换编码是利用正交变换来实现图像压缩编码的方法。通常把图像在水平方向和垂直方向上分为若干子区，每个子区有4×4，8×8或16×16点，以子区为单位进行变换，每个子区的全部像素值构成一个空间域矩阵。当图像数据分成一个8×8矩阵后，还必须将每个数值减去128，然后一一代入DCT变换公式中，即可达到DCT变换的目的。图像数据值必须减去128，是因为DCT转换公式所接受的数字范围是在 -128 ～ +127之间［6］。

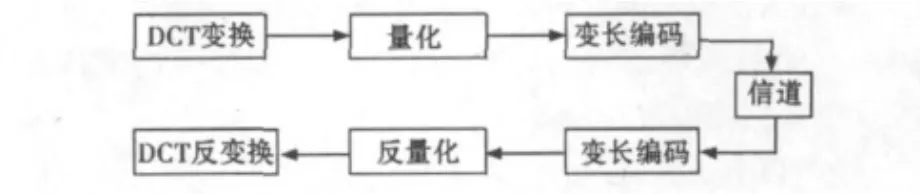
图1 DCT变换编码框图

（3）量化

在JPEG算法中，DCT变换结束后，就要进行DCT系数量化，即对二维频率系数G（u，v）进行量化。为了达到压缩数据的目的，对DCT系数需作量化处理。量化处理是一个多到一的映射，它是造成DCT编解码信息损失的根源。在JPEG中采用线形均匀量化器，量化定义为对64个DCT系数除以量化步长，四舍五入取整。同时在JPEG图像压缩中也可以采用非均匀量化。

量化后的系数要重新编排，目的是为了增加连续的“0”系数的个数，就是“0”的游程长度，方法是按照Z字形的式样编排。

DCT变换后低频分量多呈圆形辐射状向高频率衰减，故可以看成按Z字形衰减。因此，量化系数按Z字形扫描读数，这样就把一个8×8的矩阵变成一个1×64的矢量，频率较低的系数放在矢量的顶部。

（4）DC系数的编码

8×8子块的64个变换系数经量化后，按直流系数DC和交流系数AC分成两类处理。坐标u=v=0的直流系数DC实质上就是空域图像中64个像素的平均值［7］。抽样值和预测值非常接近（因为相关性强），预测误差的可能取值范围比抽样值变化范围小。所以可用少几位编码比特来对预测误差编码，从而降低其比特率，这是利用减小冗余度的办法，降低了编码比特率。

因此，对DC系数编码进行差分脉冲编码就是对相邻图像块之间量化DC系数的差值（Delta）进行编码，即对相邻块之间的DC系数的差值DIFF=DCi-DCi-1编码。

（5）AC系数的编码

量化AC系数的特点是1×64矢量中包含有许多“0”系数，并且许多“0”是连续的，因此使用非常简单和直观的游程长度编码（RLE）对它们进行编码。

63个AC系数采用行程编码的方式进行编码的格式如图2所示:

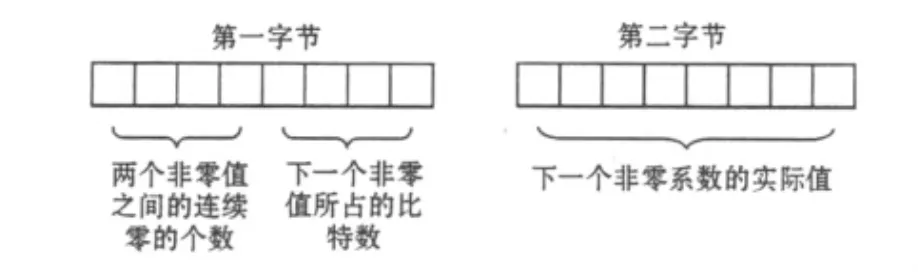
图2 AC编码格式

（6）组成位数据流

JPEG编码的最后一个步骤是把各种标记代码和编码后的图像数据组成一帧一帧的数据，这样做的目的是为了便于传输、存储和译码器进行译码，这样组织的数据通常称为JPEG位数据流（JPEG bit stream）。

经过以上过程，原始图像得到很大程度的压缩。压缩以后的数据，对于图像数据的存储来说，节省了存储空间，使得原有的存储设备，能够用来存储更多的信息。而对图像的传输而言，则减少了传输率，节省了传输时间，解决了数据量大和带宽有限的问题。

2 图像质量的评价

图像质量的正确评价是图像信息工程领域内一项很有意义的研究课题，目前常用的评价方法主要有两种，即主观质量评价和客观质量评价。主观评价方法就是让观察者对同一幅图像按视觉效果的好坏进行打分，并对其进行加权平均。这种评价结果符合人的视觉感受，相对于客观评价方法是可靠的，但它使用起来不方便，所以大多数情况下还是以客观评价方法对图像质量进行评价。

客观评价方法是用恢复图像偏离原始图像的误差，来衡量图像恢复的质量，最常用的有均方误差（MSE）和峰值信噪比（PSNR），其中MSE的表达式为:

式中{fy}{10lg分别表示原始图像和恢复图像。

而PSNR本质上与MSE相同，其表达式为:

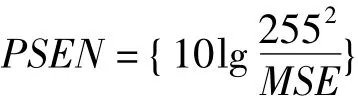
3 JPEG基本算法结果及分析

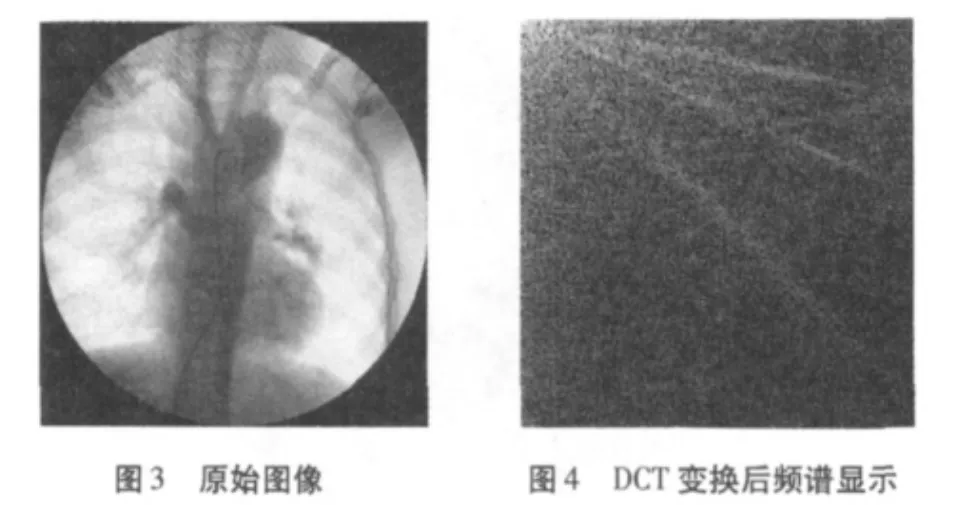
经过变换之后，变换域中总能量不变，但能量将会重新分布，在空间域中，能量分布具有一定的随机性。同时由于能量集中于零空间频率和低空间频率所对应的变换域矩阵元素中，我们对这些元素分配较多的比特数，而对能量较少的元素分配较少的比特数或不分配比特数，由于相关性的减少，变换域中分配的总比特数可以比原图像的总比特数少，这样就可以使图像所需传送的比特数减少，达到压缩的目的。

由图4图像可知，DCT变换具有能量集中的性质，数据集中在左上角。因此进行图像压缩时离散余弦变换矩阵可以舍弃右下角的高频数据。

图5 原始图像

图6 解压图像

图6是经过标准量化表后的复原图像，达到了图像压缩的一定效果。标准量化表中高频部分对应的量化值大，目的就是将高频部分编程接近于0，以便以后处理。同时经过实验表明JPEG可以在压缩比和图像质量间作取舍。方法就是改变量化值。如果量化值放大一倍，则有更多的系数量化为0，提高了压缩比。

4 基于小波变换的图像压缩

尽管基于分块DCT变换编码的JPEG图像压缩技术已得到了广泛的应用，然而在低比特率压缩时，这种编码的一个主要缺点是产生方块效应，严重影响解码图像的视觉效果。经过实验表明基于小波变换的低比特率压缩图像的后处理技术能有效地减少方块效应和保留图像的重要边缘，并且具有计算复杂性较小的优点。图像小波变换具有多分辨率的特性和时频局部化特性，它在兼顾图像噪声平滑和图像边缘检测方面表现出良好的性能，因此十分适合解决JPEG压缩图像的去方块化问题。

实验表明JPEG图像的高频量化噪声主要表现在第一级小波分解的高频分量，并且有明显的结构性质，即在第一级小波分解的高频分量显现明显的块状效应，而在第二级小波分解的高频部分和低频部分中则几乎没有表现，因此对第一级小波分解的高频分量方块边缘及其领域的像素进行平滑，可以有效减少表现为高频噪声的块状效应。

5 总结

本论文所做的主要工作是研究JPEG压缩算法以及对JPEG压缩算法进行改进，用MATLAB对其仿真，并对结果进行分析。利用医学图像实现了基本的JPEG图像压缩。由于经过JPEG基本算法压缩的图像有严重的方块效应，严重影响解码图像的视觉效果。所以对JPEG算法进行了改进。通过图像增强的方法可以使压缩后的图像的方块效应得到改善，但是图像比较模糊。通过小波变换代替JPEG算法中的DCT变换不仅使图像的方块效应得到改善，而且具有比较好的视觉效果。

［1］于晓宇，傅志中.JPEG标准下图像压缩算法的研究与实现［G］.2008年中国西部青年通信学术会议论文集，2008:336-340.

［2］贾克斌，沈波.实现医学影像存档和传输系统中的若十关键技术［J］.中国图象图形学报，2000，5（7）:539-544.

［3］Rafael C.Gonzalez，Richard E.Woods.Digital Image Processing［M］.北京:电子工业出版社，2007:326-412.

［4］余秋菊.基于DCT变换的JPEG图像压缩及其MATLAB 实现［J］.科技信息（学术研究），2008（36）:557.

［5］暴晋飞.一种抗JPEG压缩的数字图像水印算法［J］.重庆邮电大学学报，2009，21（6）:55-59.

［6］Singh S，Kumar V，Verma HK.DWT-DCT Hybrid Scheme for Medical Image Compression［J］.Journal of Medical Engineering ＆ Technology，2007，31（2）358-371.

［7］Sukhwinder Singh，Vinod Kumar，H.K.Verma.Reduction of Blocking Artifacts in JPEG Compressed Images［J］.Digital Signal Processing，2007.