线性移位寄存器在图像加密中的应用
荆 锐,朱 平,杨恒欢,冯 涛
(1. 上海中新科技管理学院计算机系,上海200023;2. 上海第二工业大学成人与继续教育学院,上海200041)
线性移位寄存器在图像加密中的应用
荆 锐1,朱 平2,杨恒欢1,冯 涛2
(1. 上海中新科技管理学院计算机系,上海200023;2. 上海第二工业大学成人与继续教育学院,上海200041)
图像加密技术作为数字信息保护的一种有效手段,随着信息技术的发展,人们对其安全性的要求越来越高。讨论了关于线性移位寄存器(LFSR)在图像加密中的应用。本算法先采用LFSR算法产生伪混沌比特密钥流,将该密钥流作为随机值映射算法和加密算法的初始参数。随机值映射算法取其中较高位的密钥流,生成置乱序列用于图像像素的位置置乱。另一组密钥流作为加密序列可对图像的像素值进行加密。实验结果表明该方法运算速度快,通过随机值映射算法产生的伪随机置乱和加密序列具有很强的可操作性、保密性,而且截取伪混沌比特密钥流的位数也可作为密钥存在。
线性移位寄存器;比特密钥流;随机值映射算法
0 引言
随着数字技术和电子商务的迅猛发展,信息传输的安全性变得越发重要,其中数字图像的信息安全引起了人们的密切关注。据美国科研人员的研究成果,图像和电子邮件为隐藏和传送信息提供了更多的机会,数字图像保密技术作为数字图像信息保护的有效手段,人们对其安全性的要求也越来越高。目前,主要有三种数字图像的安全保护技术。
0.1 空间置乱技术
数字图像空间置乱技术是数字图像加密的一种方法。图像置乱的功能是将图像中像素的空间位置打乱,将原始图像变成一个杂乱无序、不可见的新图像。基于置乱技术的图像加密技术一般可以认为是对图像矩阵进行有限步长的初等矩阵转换,以此打乱图像像素的排列位置,达到图像加密的目的。
目前流行的置乱方法有:
(1) Arnold变换。它是一种常用方法,基本上是连接和裁剪矩阵的过程,将数字图像矩阵中的像素位置重新排列。根据图像矩阵是有限点集的特点,这种不断排列的结果由于动力系统固有的特性,在迭代到一定步数时会恢复到原来的图像矩阵,即变换具有庞加莱回复性或周期性。随着图像的增大,周期变大,然而单次置乱所需的计算量急剧增大,导致同样置乱效果所需的迭代次数增加,而且,使用穷举法迭代即可轻易破解,所以该方法不能满足现代加密、解密的要求,通常仅用做预处理[1],或者与其他方法混合加密[2]。
(2) Hilbert曲线变换。这是由德国数学家Hilbert给出的填满一个单位正方形的FASS曲线[3]。影响其置乱效果的因素主要有置乱路径和置乱周期。
如图1所示,在一张3×3的图像中各像素按图中曲线走向作位移,遍历所有点就可生成一副置乱后的图像。每个方阵图像(大于等于2×2)都有多种FASS曲线,所获得的结果都是不同的,因此可通过多周期的不同曲线来组合置乱图像以提高安全性。此外,空间置乱技术还有Fibonacci变换和骑士巡游变换等方法。
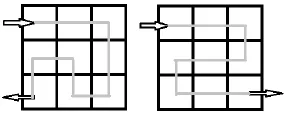
图1 (a) Hilbert曲线1 (b) Hilbert曲线2Fig.1 (a) Hilbert line 1 (b) Hilbert line 2
0.2 像素变换技术
数字图像像素变换技术是通过将图像各像素的灰度值改变,来达到隐藏图像的目的。现有的像素变换方法大多基于混沌理论,其中应用最为广泛的是Logistic映射。如文献[4]提出了一种基于离散数字混沌序列的图像加密方法。文献[5]在Logistic映射的基础上,采用3个由离散数字混沌序列进行异或运算获得长周期的离散数字混沌序列,将产生的混沌序列用于图像的加、解密。混沌加密方法的安全性主要取决于密钥流产生器所产生的信号与随机数的近似程度,密钥流越接近随机数则安全性越高,但由于现今的混沌技术只能产生伪随机数,故安全性较低。
0.3 数字水印技术
目前针对图像数据的水印算法繁多,现有的数字水印嵌入方法主要有:空域算法、变换域算法等。文献[6]中采用的空域算法是通过用密钥的方式控制水印嵌入,以保证水印分布在图像中多处不同位置,由此来提高水印的鲁棒性,但对于图像的抗旋转、抗裁剪能力较弱。基于二维离散余弦变换的变换域方法的主要思想是在图像的DCT2变换域上选择中低频系数叠加水印信息。数字水印技术存在水印的鲁棒性与不可见性的矛盾,目前没有更好的方法使这对矛盾得到完美的平衡。
1 背景技术介绍
1948年香农(Shannon)从理论上证明:如果密钥流序列是一真正的随机序列,那么相应的流密码就是绝对安全的,即实现了完善保密性。但是一个随机序列是无法完全得到的,只能用伪随机序列来代替随机序列以达到相对安全的目的。在信息安全的许多应用领域,都需要伪随机数发生器产生长周期的随机整数序列,这些整数或者作为隐藏秘密信息的位置索引,或者作为加(解)密运算的密钥。一般可认为伪随机序列的随机性越高,其加密信息在对抗如剪裁、噪声等攻击后的还原效果越好。
在保密通信中,为了提高流密码的抗攻击能力,密钥流通常需满足以下三个要求:大的线性复杂度、不可预测性和长周期[7]。传统的信息加密方法可分为分组密码和序列密码。序列密码的安全性要高于分组密码。LFSR是产生序列密码的方法之一,其反馈函数是寄存器中某些位的简单异或所得,这些位也称之为抽头序列。由于其反馈函数为线性,因此称为线性反馈移位寄存器(LFSR∶line feedback shift register)。一个n位的LFSR能够产生2n-1位长的伪随机序列。一个n级线性反馈移位寄存器(FLSR)由一个n位寄存器r = r0,…, rn-1和一个n位的抽头序列t = t0,…, tn-1组成。为了得到密钥的一个位,要利用rn-1,使寄存器向右移动一位,并且插入新的比特(位)(r0t0⊕ … ⊕rn–1tn–1)。假设四级FLSR的抽头序列为1001,寄存器的初始值是0010,抽取密钥流和寄存器的值做异或,第一次生成的值为0001(寄存器向右移1位得0001),密钥为1,循环重复,第二次的密钥为01,一直到一个周期结束。下表通过LFSR产生的是周期为15的密钥流,010001111010100是最终产生的密钥流。LFSR方法可以通过使用少量信息来产生较长的密钥序列,以模拟一次一密,其生成的密钥流满足流密码的三个要求。密钥生成过程如表1所示。
本文先采用LFSR算法产生伪混沌比特密钥流,将该密钥流作为随机值映射算法的初始参数。随机值映射算法分别按不同位数截取伪混沌比特密钥流并产生两种数据序列,将其中一个作为置乱序列可用于图像像素的位置置乱,其二作为加密序列可对图像的像素值进行加密。实验结果表明,本文算法所生成的置乱结合加密的图像加密程度高,还原损耗低,在运算量和安全性上达到了很好的平衡。

表1 LFSR密钥流生成表Tab. 1 The table of LFSR key generation
2 基于混沌加密和移位寄存器的图像加密算法
本文算法通过线性反馈移位寄存器(LFSR)生成两种不同位数的伪随机密钥流,作为随机值映射算法的初始参数,其中生成的10 bit密钥流作为置乱序列用于图像位置置乱;同时,其中生成的8 bit密钥流作为加密密钥,与置乱后的图像做异或运算,得到混合加密图像,在解密时只需要将加密后图像重新代入上述算法即可得到原始图像。算法包括四部分:1) 载入初始数据并归一化;2) 生成LFSR密钥流;3) 随机值映射置乱;4) 图像像素加密。流程图见图(3)所示:

图3 加密流程图Fig. 3 Flow diagram of encryption
2.1 载入初始数据并归一化
需要载入的数据有原始图像和用户密钥。由于图像信息的数据格式与系统做运算时的数据格式不符,须进行归一化操作才能够再加密。初始读入的灰度图像数为二维矩阵,是数值范围为0~255的整型数据。将图像格式转为一维向量M,其像素数值以1/256为阶,范围在0~1之间的Double型数据与本文中加密时密钥的范围相同。图像归一化使得图像像素之间的差异性降低,对数据加密所需变化的要求更小。
2.2 生成LFSR密钥流
在本文算法中的图像置乱和图像像素加密算法,都需要定义初始条件参数初始条件参数直接关系到最终图像的加密效果。在本文算法中,与图像进行置乱或加密的伪随机密钥流的长度至少要长于原始图像一维向量M。本文通过用户输入初始密钥,确定LFSR的初始参数(寄存器级数),可生成所需长度的密钥。
传统LFSR算法的抽头序列和寄存器初始值是由密钥发生器生成的随机数确定,其密钥长度由寄存器级数确定。在传统LFSR的加密算法中,需要记录运行移位寄存器和密钥算法发生器的时钟,即在不同时间所得的随机值是不同的,数据恢复所需时钟应与其同步。由于需要严格同步,因此计算复杂、运算量大且速度慢。本文通过用户控制初始参数确定时钟,同时增加寄存器级数,以获得较长的密钥流,该方法计算简单、速度快。其具体流程如下:
1) 判断用户输入密钥(Lkey)大小,如果密钥Lkey数值过低则采用系统默认值(Lkey= 32);
2) 将Lkey数值输入至时钟,生成伪随机数列R1(数值范围0~1的double型)和抽头序列R2(序列中各数值为0或1);
3) 将R1转为二进制,生成二值序列R1’,以Lkey数值作为循环数,将R1与抽头序列R2做异或循环,得到足够长的二值LFSR密钥流;
4) 将所得的二值LFSR密钥流以n(n ≥2)位截段转为密钥流K(double型数据),n为可控参数。
为了取得更高的安全性,在步骤4) 中根据截断位数不同可产生不同的密钥流,在本文算法中,生成的第一个密钥流K1是以n =10,即10位截断所得,第二个密钥流K2,则是以8位截断所得。K1与K2密钥流有很大的差异性,可极大地提高安全性。
本方法将随机值的确定和用户密钥联系起来,可相应扩大密钥的循环范围以及密钥复杂度。如果将此处生成的伪混沌二值密钥流直接用于加密图像,虽能取得一定的加密效果,但其安全性较低。因此,本文仅将其用作后续算法的初始条件,通过后续算法更加接近混沌的密钥流。这样加密的图像安全性更高,几乎不可能被强制破解。
2.3 随机值映射置乱与图像像素加密
本文提出一种简单解决上述安全性问题的方法,以2.2中截断位数为10位所产生的十进制密钥流K1作为初始条件,将其重新排序(由大到小)并记录其元素排序位置变化。按K1的排序位置将原始图像像素的空间位置映射到对应位置,得到置乱的图像。最后将置乱后的图像与另一个8 bit的十进制密钥流K2异或加密,取得混合加密效果,其流程如下:
1) 建立与所需加密图像M等长的图像空间序列S,记录S的原始空间位置;
2) 由系统将2.2中生成的10bit伪混沌密钥流K1作循环运算;寻找K1中的最大值并将其赋值为−1,将找到的最大值的位置对应记录到向量S中;重复循环,直至K1中均为−1;
3) 将图像向量M像素的空间位置按变换矩阵S映射,得到图像向量M1,置乱完成;4) 将图像向量M1与8 bit十进制密钥流K2异或加密,得到加密图像M2,加密完成。本文置乱算法采用的是8 bit密钥流和10 bit密钥流复合加密置乱图像,安全性高,相对传统LFSR计算机的计算量小。如果还需要提高安全性,可增加置乱所需密钥的比特位数。
3 试验结果与结论
本算法采用测试图像为“世博会中国馆”图像,像素数大小为128×128,计算机硬件为CPU 2.6GHz;内存512MB;软件环境为WINDOWS-XP, MATLAB 7。输入的用户密钥为默认值32。所需时间包括绘图时间,结果取小数点后3个有效位。试验中分别对图像做了两种测试。
1) 进行先置乱后加密及先加密后置乱两种测试,测试结果见表2。从表2可得:先置乱后加密与先加密后置乱得到的混合加密图像虽然不同,但是加密效果是几乎一样,都有着较高的不可见性,并且两者所需的运行时间几乎相等。

表2 测试表1Tab. 2 Test table 1
2) 在不同位数密钥的初始条件(K1分别为6bit、8bit、10bit; K2为8bit)下置乱加密图像,与Arnold置乱效果作对比,测试结果见表3。由表3可得:传统Arnold加密对本图像的Arnold变换次数至少需要140次(变换次数对运算时间影响很大),才能取得与本文算法相近的加密效果,此时运算时间略多于本文算法,如果需要较好的置乱效果,效率较差。 本文算法只需要很短的密钥就可取得良好的加密效果,密钥比特位越长,置乱加密效果越好,并且增加置乱算法密钥位数对计算量的增加不明显。

表3 测试表2Tab. 3 Test table 2
[1] SUJATHA S S, MOHAMED SATHIK M. Feature based warermarking algorithm by adopting arnold transform[J].ICT,CCIS, 2010, 101: 78-82.
[2] 冯茂岩, 冯波, 沈春林. 基于分块DCT变换和Anrold置乱的自适应图像水印算法[J]. 计算机应用, 2008, 28(1): 171-173.
[3] 齐东旭. 分形及计算机生成[M]. 北京: 北京科学出版社, 1997.
[4] 陈帅, 钟先信, 石军锋,等. 基于离散数字混沌序列的图像加密[J]. 电子与信息学报, 2007, 29(4): 898-900.
[5] 黄晓生, 顾景文. 基于复合混沌序列与小波变换的图像加密算法[J]. 计算机工程, 2007, 33(14): 128-135.
[6] 陈灏. 空域数字图像水印算法研究与实现[J]. 现代电子技术, 2007, 30(10): 149-165.
[7] BETH T, PIPER F C, The Stop-and-Go Generator[C]//Proc of the EUROCRYPT 84 Workshop on Advances in Cryptology Theory and Application of Cryptographic Techniques, Paris France, 1984: 88-92.
The Application in Image Encryption by Line Feedback Shift Register
JING Rui1, ZHU Ping2, YANG Heng-huan1, FENG Tao2
(1. Department of Computer, Shanghai Science and Technology Management College, Shanghai 200233, P. R. China; 2. School of Adult and Continuing Education, Shanghai Second Polytechnic University, Shanghai 200041, P.R.China)
For digital information protection, image encryption is an effective technology. As the development of information technology, people also need more and more security on image encryption. This thesis discussed the application in image encryption by line feedback shift register. At first the system generated the initial pseudo-chaos bit key stream by LSFR. The key stream becomed the initial parameter of the random value mapped scrambling algorithm and chaos encryption algorithm. Mapping the image with the mapped stream which was generated by the random value mapped scrambling algorithm with the higher digital key stream, then encrypted the image with the encrypted stream which was generated by another key stream. The result shows this system runs fastly. The pseudo-random mapped stream and pseudo-encrypted stream that were generated by the random value scrambling algorithm both had a strong operational, confidentiality. Also the chosen pseudo-chaos bit key stream can become the keywords.
Line Feedback Shift Register; bit key stream; random value scrambling algorithm
TP391.41
A
1001-4543(2011)04-0293-05
2011-04-06;
2011-10-05
荆锐(1987-),男,吉林省吉林市人,学士,主要研究方向为图像图形学应用与信息系统安全,电子邮箱jingrui110@hotmail.com

