一种黑洞数和Logistic混沌序列的图像加密应用
杨恒欢,冯 涛,荆 锐
(1. 上海中新科技管理学院计算机系,上海 200023;2. 上海第二工业大学成人与继续教育学院,上海 200041)
一种黑洞数和Logistic混沌序列的图像加密应用
杨恒欢1,冯 涛2,荆 锐1
(1. 上海中新科技管理学院计算机系,上海 200023;2. 上海第二工业大学成人与继续教育学院,上海 200041)
图像加密技术是数字信息保护的一种有效手段。在信息技术的发展下,人们对图像信息安全性的要求越来越高。本文提出了一种基于黑洞数和Logistic混沌序列的图像加密算法。本算法通过对黑洞数的研究,利用黑洞数发生器产生伪混沌序列,将该序列作为初始参数代入logistic算法,产生混沌密钥流对图像进行加密。实验结果表明该方法运算速度快,产生的置乱和加密序列的安全性很高。
黑洞数;logistic算法;图像加密
0 引言
随着互联网技术与多媒体技术的飞速发展,越来越多的信息通过网络来进行传输。数字图像已经成为人们进行信息交流的一种重要的信息载体。图像加密技术是多媒体信息安全的核心技术,是数学、密码学、计算机视觉等多学科交叉的研究课题。其中密码学主要是研究通信安全保密的学科,是保护信息在信息的传递过程中不被敌手窃取、解读和利用的主要方法。数学中有很多公式和方法被应用于其中,凡是具有混沌特征的算法都可应用在加密领域。
混沌现象最早由美国气象学家Lorenz E T 发现。他在1963年进行数值实验时,利用计算机模拟天气变化,发现了系统变化的非周期性和不可预测性之间的关系,给出了一个三变量自治方程(Lorenz方程)来描述混沌现象,并提出了用蝴蝶效应来表达系统长期行为对初值的敏感依赖性。混沌系统还有遍历性和内随机性[1]。初值的敏感依赖性体现为:混沌算法产生的序列,随着初始值的微小变化,将具有非常大的差异性。遍历性和内随机性体现为混沌系统生成的序列分布是离散的。混沌系统的性质十分适合加密领域,并且具有很好的适用性和安全性。因此,现今的加密技术主要以混沌系统作为主要研究方向之一。目前数字图像加密所用的混沌系统主要有:
(1) Logistic映射,是实际系统中存在的最简单的非线性差分方程之一。这是一个动态系统,由于系统在运行过程中表现出混沌行为,因此在许多领域中都被研究和应用,其公式如下:

其中λ称为分枝参数,当λ=2.8时,系统表现出存在两个周期点;当,出现四个周期点。随着λ的逐渐增大,存在的周期点数也越来越多,并且频率越来越高,直到达到极限值3.569 945 6…。当3.569 945 6…<λ≤4时,映射处于混沌状态,其产生的序列{xi}是非周期不收敛,随着初始值的不同有着非常大的差异性。该系统初始状态x1在(0, 1)中随机取值作为迭代初值,通过公式(1)对这个初始值进行迭代,当λ>3.569 945 672…时,系统进入混沌状态。Logistic映射所构建的密钥序列具有良好的随机性和初值敏感性。
(2) Chebychev混沌序列,以K为映射基数的Chebychev公式如下:

当K= 6时,方程处于混沌状态,所产生的序列{xn}为混沌序列。系统在空间的相邻轨道间收敛或发散的平均指数率(Lyapunov)为1.791 733…。文献[2]通过Chebychev多项式的混沌映射构建了加密质量控制模型,并进一步构造了图像小波域加密算法。该方法简单易行,兼容性高,但在透明性与运算时间上难以取得较好的平衡点。
(3)正弦映射,Sin方程在某种条件下亦可生成混沌序列,公式如下:

当λ= 0.99时,系统处于混沌状态,将初始值x1带入,可获得序列{xn}。序列{xn}中的元素值呈混沌分布且离散。由于正弦方程较为简单,其运算速度很快,但易被破解,往往需要与其他算法相结合才能达到一定的安全性。如文献[3-4]都是利用正弦混沌映射和Logistic映射相结合对图像进行加密的方法,但在传输及还原过程中容易造成一定的图像损失。
本文算法通过引入数论中的黑洞数,根据其数学特征产生具有一定混沌特性的短序列,结合Logistic映射将图像进行加密。实验结果表明该方法简单有效,加密后的图像具有很好的混沌特征,而且计算速度快、安全性高。
2 黑洞数以及其性质
黑洞数问题是近几十年内出现的有趣数学问题,引起了国内外数学界的广泛注意和研究[5-7]。数论中对于黑洞数定义为:在含有未知数变量x的代数式y = f (x)中,当变量x任意取值时,其应变量y都不改变,此时称应变量y为黑洞数(数组)。本文主要在重排求差黑洞数的基础上介绍产生伪混沌序列的方法,并应用于图像加密。
重排求差方法:任意数字不完全重复的整数x(像33, 555, 777 7等都应该排除),经有限“重排求差”操作,总会得某一个或一组黑洞数y。重排x得到的最大数减去重排x得到的最小数,不断循环此过程,直到落入循环,此循环内的数称为黑洞数(数组)。下表中列出部分数字重排求差流程及结果。

表1 重排求差流程及结果Tab. 1 The Process and results for number with potentiometer
文献[8]通过数学论证,证明了黑洞数具有3个性质:1) 黑洞数一定能被9整除;2) 奇数黑洞数(位数≥3)定能被99整除,且中间位数字为9;3) 任意黑洞数,其首末位的数字和为10,或者和为9且中间的所有位数皆为9。
本文作者在此基础上作了大量的数据分析研究,发现了更多的规律。
规律1
1) 任意位数为偶数(大于2)的黑洞数定能被9整除,首末位数字的和为10,如:表1中x =851 742和x=860 832的黑洞数组;
2) 任意位数为奇数(大于2)的黑洞数定能被99整除,且中间数字为9。如:表1中x =82 962和x =8 429 652黑洞数组;
3) 对于任意黑洞数必定首末位和为10或者9,和为9时所有中间位数必定都为9。如:黑洞数495。
为了叙述简便,本文加入了边的概念:
定义 当一个数满足规律1中黑洞数性质时,则认为此数字在落入黑洞数的边上或者黑洞数中。
规律2 当一个数落入黑洞数的边上或者黑洞数中,通过对此数字的重排求差运算,很快能得到此数字产生的所有黑洞数。如:表中6 619 974为首末位为10的非黑洞数,符合规律1条件,只需2次重排求差计算就落入黑洞数。
规律3 对于任意数字x,在重排求差运算至第二次落入黑洞数前,运算过程中所得到的数字序列中所有数字都只出现一次。不同的数字间,在落入黑洞数的边之前,所得数字集合必定不同。如:表1中的所有初始数字,其取落入黑洞数的边之前的数字均不相同。
黑洞数的性质与规律,表明了对任意数字,其重排求差运算过程中直到第二次落入黑洞数前,得到的数字是无序、离散、无重复项的混沌序列。随着不同的初始值,运算所得的数据具有很大的差异性。对于位数较低的x,其黑洞数相对较少,长度较短,无法取得足够长度的混沌序列,并且黑洞数边上的数字具有快速落入黑洞数的特性。因此,本文算法为提高安全性,由随机数发生器生成长度超过10位的初始值x,然后将x代入黑洞数发生器取得伪混沌的运算轨迹序列,最后将伪混沌序列递入logistic算法产生足够长的混沌序列对图像置乱加密。
3 基于黑洞数序列和Logistic的图像加密算法
本文算法通过黑洞数发生器生成具有混沌性质的短密钥流,将其作为Logistic算法的初始值,生成混沌密钥流,截取与图像相同长度的加密密钥流。最后将归一化的加密密钥流与置乱后图像做异或,得到混合加密图像。算法包括3部分:1) 黑洞数发生器生成短混沌序列;2) Logistic混沌加密;3) 图像解密。流程图如图1所示:
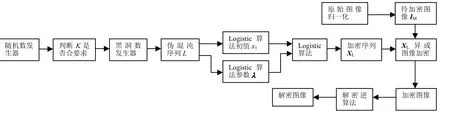
图1 程序流程图Fig.1 Program flow diagram
3.1 黑洞数发生器生成伪混沌序列
由于图像信息的数据储存格式与系统做运算的格式不符,须先对图像进行归一化操作才能再加密。将灰度图像读入后可得到一个M*N大小的二维矩阵I,其中各元素是范围为0~255的整型数据。将I降维为一维图像矩阵IM,其元素数值是以1/256为阶,范围为[0, 1]的Double型数据。图像归一化使得图像像素之间的差异性降低,对加密的要求降低。
通过实验发现,对于初始值K,如果其位数越短,黑洞数发生器可计算的步骤越少,不足以产生足够长的密钥流,并且K直接在黑洞数边或黑洞数上的几率较大;当K超过8位,大多随机数可产生足够长度的密钥流,即使不同的K皆落在同一黑洞数(组)上,不同数字落入的黑洞数组的位置也极有可能不同,甚至落入不同的黑洞数(组)中。所以K的位数越高,安全性越高。本文认为K位数超过10时最佳,在长度超过10的情况下,只要不是黑洞数中的数值,即使K与某个黑洞数的边相邻,发生器产生的序列也是非常安全的。
由随机数发生器产生一个位数大于10的初始数K,K中每个位的数字不能完全相同。为保证黑洞数发生器能取得尽可能长的伪混沌序列,先检测K是否在黑洞数和黑洞数边上。对于不符合要求的K,则由随机数发生器重新生成K。符合要求的K将作为提取密钥反馈给用户,然后将K作为黑洞数发生器的初始值代入,运行黑洞数发生器并记录每次运算结果,直到运算落入第二次循环时跳出。所记录的数值即为伪混沌序列L,黑洞数发生器生成伪混沌序列操作完成。判断黑洞数边的公式流程如下:

步骤1 将密钥K看作由n (n ≥10)个一位数组成的数组K ={a1, a2,…, an}。
步骤2 判断K是否在黑洞数或者黑洞数边上:
(1)将K的首末位a1, an代入公式(4),求首末位数字和,如果1dA值为0(1)则表示首末位和为10(9);(2)当n为偶数时,将{a1, a2,…, an}代入公式(5),判断所得2dA是否为整数;
(3)当n为奇数时,将{a1, a2,…, an}代入公式(6),判断2'dA为是否为整数且Mi为0。
如果将K代入后并不满足步骤2中的(1)和(2)或者(1),(3)时,说明K为远离黑洞数的数字。此时K代入黑洞数发生器中得到的伪混沌序列更长,不同K得到的伪混沌序列间的差异性更大。
黑洞数发生器取得序列的程序段如下:
for j =1∶30 % 运行黑洞数发生器30次
if length(K(j))~=length(K(1)) % 判断位数,如果发生器前一次取得数值如098等,则变为980后参与运算
adkey(j)=adkey(j)*10^(length(adkey(j))-length(K(1)));
end
key(1)=K(j); % 赋值给中间变量
for i=1∶len % 将变量中各位数分离,如Kn={a}转换为K ={a1, a2,…, an}
A(i)=fix(key(i)*10^(i-len));
key(i+1)=key(i)-A(i)*10^(len-i);
end
B=sort(A,'descend'); % 重新排序 降序
B1(1)=0;
for i=1∶len % 重新转换,如{a1, a2,…, an}->{a}
B1(1)=B1(1)+B(i)*10^(len-i);
end
C=sort(A); % 重新排序 升序
C1(1)=0;
for i=1∶len % 重新转换
C1(1)=C1(1)+C(i)*10^(len-i);
end
K(j+1)=B1-C1; % 将升序和降序排列做差,并记录数值给下一级Kn+1
end
初值K1通过时钟密钥key控制的随机数发生器取得,运行黑洞数发生器,从记录得到的K ={K1, K2,…, K30}中,去除循环数部分,得到的K ={K1, K2,…, Kn}即为所求的伪混沌序列。
3.2 Logistic混沌加密
本文将伪混沌序列L中元素进行归一化,使序列L中的每一个数据都符合logistic混沌算法的要求,然后将所有数据分别代入logistic公式,取得多组混沌序列,将其相连并根据图像IM的大小截取相同长度,得到加密序列XL,将图像像素加密。此方法的实现较为简单,加密流程如下:
步骤1 将L = (L1, L2,…, Ln)中数据进行归一化操作,先全部转为0 ~ 1之间的double型数据,取8位有效数字,如3 847 243 8370.384 724 4,得到L'= {L'1, L'2,…, L'n}。然后将L'n代入公式(7)变换,得到一组logistic参数λ,λ={λ1,λ2,…,λn}。

步骤2 将L'和λ的元素按组(如L'1和λ1)代入logistic公式(1)并做迭代。迭代次数i由公式(8)取得:ceil为截尾取整,如果有小数则在取整后加1。将公式(1)迭代i次,记录每次结果,去除前30个数据。代入所有的L'和λ可得到n组混沌密钥流,根据图像大小截取相同长度的密钥流,合并为图像加密矩阵XL。

步骤3 将混沌加密矩阵XL与图像像素值做异或运算生成加密图像。异或公式见公式(9):

步骤4 将所得的置乱图像I 'M由一维矩阵转换成二维矩阵,至此图像IM经过混合加密得到加密图像I 'M,加密算法结束。
3.3 图像解密
图像解密的步骤与加密步骤类似,先将提取密钥key带入随机数发生器取得K,将K和加密后的图像I 'M代入加密逆过程,把K作为初始值代入黑洞数发生器,产生伪混沌序列L',然后将伪混沌序列L'代入Logistic加密算法取得解密序列XL,将XL与图像I 'M做异或,提取解密图像。
4 试验结果与结论
本文系统测试选择的图像为“上海SSPU”,像素数大小为256×256,硬件测试环境为CPU 2.6GHz;内存512MB;软件环境为WINDOWS-XP, MATLAB 7.9.0。测试结果见表2。

表2 测试结果Tab. 2 The results for test
选择输入的时钟密钥为20,分别对图像进行了加密及置乱,解密效果显示:无论是先加密后置乱,还是先置乱后加密,加密后的图像都有着较高的安全性。仿真结果表明,该算法运算速度较快,具有较高的抗攻击和抗干扰能力,有一定的实用性。
测试结果表明,黑洞数发生器足以产生一定长度的密钥流,结合Logistic进行混沌加密的图像能够达到很好的加密效果,具有很高的安全性,随机数发生器产生的随机数x的位数对系统运行时间的影响较小,总体的运算时间极少。
[1] 唐巍, 李殿璞, 陈学允. 混沌理论及其应用研究[J]. 电力系统自动化, 2000, 24(7): 67-70.
[2] 何希平, 朱庆生. 基于混沌的图像小波域加密算法[J]. 计算机应用, 2007, 27(8): 1895-1897, 1900.
[3] 陆秋琴, 马亮. 基于logistic映射和正弦混沌映射的交替混沌加密算法[J]. 科技信息: 学术版, 2008(12): 106-108.
[4] 许小勇, 樊继秋, 熊思灿. 一种基于双混沌序列的数字图像加密算法[J]. 科学技术与工程, 2010, 10(29): 7307-7309, 7333.
[5] KRAUSE R M, MILLER N, TRIGG C W. Solutions of elemientary problems(Kaprekar's Constant)[J]. American Mathematical Monthly, 1971(78): 197-198.
[6] ELDRIDGE K E, SAGONG S. The determination of Kaprekar convergence and loop convergece of all three-digit numbers[J]. American Mathematical Monthly, 1988(95): 105-112.
[7] 杨之, 张忠辅. 角谷猜想和黑洞数问题的图论表示[J]. 自然杂志, 1988(6): 453-456, 480.
[8] 黄振国. 黑洞数的性质与它神奇的衍生法[J]. 广西大学梧州分校学报, 2004(1): 62-64.
An Application in Image Encryption Algorithm By Black-Hole Numbers and Logistic Chaos Sequence
YANG Heng-huan1, FENG Tao2, JING Rui1
(1. Department of Computer, Shanghai Science and Technology Management College, Shanghai 200233, P. R. China; 2. School of Adult and Continuing Education, Shanghai Second Polytechnic University, Shanghai 200041, P. R. China)
As the development of information technology, people need more security on image safety. Image encryption is an effective technology for the digital information protection. This thesis introduces a new image encryption algorithm based on Black-hole numbers and Logistic chaos sequence. By research the Black-hole number, it can have a chaos sequence and the chaos sequence which will be sent into Logistic algorithm as the initial parameters. Then the algorithm can generate chaotic key stream for image encryption. The result shows that the system runs fastly and security of the image encryption is very high.
Black-hole; Logistic algorithm; Image encryption
TP391.41
A
1001-4543(2011)04-0287-06
2011-04-06;
2011-10-08
杨恒欢(1988-),男,江苏无锡人,学士,主要研究方向为图像图形学应用与信息系统安全,电子邮箱yanghenghuan@hotmail.com。

