基于非结构网格的分蓄洪区水沙演进数学模型研究
张细兵,欧治华,崔占峰,孙 先
基于非结构网格的分蓄洪区水沙演进数学模型研究
张细兵1,2,欧治华3,崔占峰1,孙 先1
(1.长江科学院河流研究所,武汉 430010;2.武汉大学水利水电学院,武汉 430072;3.荆州市长江河道管理局洪湖分局,湖北洪湖 433200)
基于非结构三角形网格,采用有限体积算法,建立了分蓄洪区水沙演进数学模型。模型网格能很好适应分蓄洪区复杂的边界条件,应用了DEM数字模型插值技术,能快速获取计算域的地形数据,实现了洪水演进过程中泥沙输移和河床冲淤变形的同步模拟。模型中还对网格划分、数值离散、动边界及干河床处理等关键技术进行了研究,并提供了相应的处理方法。该模型在荆江分洪区得到成功运用,较好地复演了1954年分洪过程。洪水计算成果可为分蓄洪区防洪决策与抢险提供参考,分洪闸后最大冲刷深度计算成果可为工程设计提供参考。
非结构网格;分蓄洪区;洪水演进;泥沙冲淤;数值模拟
1 概 述
河流在自然或人工溃堤情况下,常常会有水沙的急变运动发生,洪水在洪泛区内的演进将给洪泛区内人民生命财产安全构成巨大威胁。因此,正确模拟溃坝洪水在洪泛区内的演进过程,将给防洪抢险和防洪决策提供重要的依据。由于问题的复杂性,国内外许多学者开展了分蓄洪区洪水演进的研究。如武汉大学的余明辉、张小峰[1]采用矩形网格和有限体积算法,建立了分蓄洪区洪水演进数学模型;王嘉松[2]、王志刚[3]基于矩形网格,分别采用有限差分算法和有限体积算法,对局部溃坝水流演进问题进行了研究;Macchione和Morelli[4]提出了用于求解溃坝水流的MacComack格式。国外许多商业化的软件也具备了分蓄洪区洪水演进功能,如丹麦DHI水环境研究所研制的MIKE-Flood模型能进行分蓄洪区洪水演进的一、二维嵌套模拟;美国密西西比大学研制的CCHE-Flood能进行溃坝洪水演进的模拟等。但以上模型大都采用结构化网格,一般未考虑河床冲淤变形问题。
为此,笔者在前人研究基础上,建立了分蓄洪区的水沙演进模型。其特点为,采用非结构三角形网格,能很好拟合复杂的水域边界,并能自由对重点区域进行加密处理;在模拟洪水演进的同时,还能模拟泥沙输移和河床冲淤变形,从而为分蓄洪区的洪水调度及防洪抢险提供更为丰富和准确的数据。
2 非结构网格生成技术
复杂流动问题数值计算中采用的网格,根据拓扑结构大致分为结构化网格和非结构化网格2大类。非结构化网格是一种无规则随机的网格结构,其优点为:复杂区域的网格生成自动化程度高、贴体性好;流动方程直接在物理空间上的非结构化控制体上离散和求解,不需要坐标变换和方程变换,物理空间即为计算空间;能够较方便地求解复杂边界的流动且更容易实现网格自适应处理。
非结构化网格生成方法主要有2种:Delaunay三角形化方法和阵面推进法。这2种方法均能实现网格生成的自动化;能够实现局部加密;能够加以推广生成三维非结构化网格。笔者基于阵面推进法,引入了背景网格(Background Mesh)概念,提出了河道有限元网格自动剖分方法[5]。
3 非结构网格上的数值求解方法
3.1 基本方程及其离散
非结构化网格的方法不需要进行坐标转换,物理空间即为计算空间,因此可采用单一物理坐标系描述流动方程和计算方法。
3.1.1 基本方程
建立在静水压强假定下的平面二维笛卡尔坐标系中的水沙运动方程可写为:
连续性方程
水流运动方程

悬沙运动方程
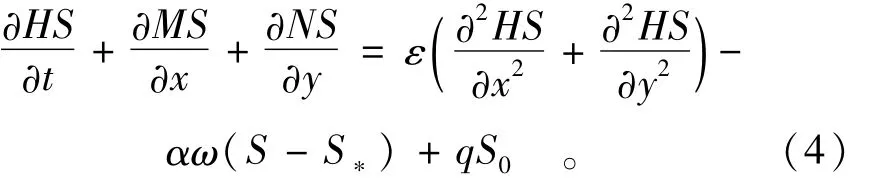
河床变形方程
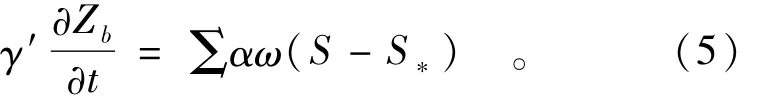
式中:H为水深(m);u和v分别为x和y方向的流速(m/s),M=uh,N=vh;Z为水位(m);u0,v0,S0分别为源项流速分量和含沙量;n为Manning糙率系数;vt为紊动粘性系数;q为单位面积上水流的源汇强度(m/s);ρ为水体密度(kg/m3);S为含沙量;S*为挟沙力;ω为泥沙颗粒沉速(m/s);γ′为泥沙干密度(kg/m3);α为恢复饱和系数;ε为泥沙扩散系数。
方程(1)-(4)可写成以下统一形式,

式中:φ={H,M,N,HS};xi={x,y};Γφ为广义扩散系数;Sφ为源项。
3.1.2 方程离散
为保证满足动量方程守恒,基矢量一般采用总体直角坐标(即对整个计算区域设定直角坐标系)中的速度分量。本文的节点布置方法采用单元中心法,网格为同位网格。对于任意形状的控制体,方程(6)的控制体积法的积分形式如下,
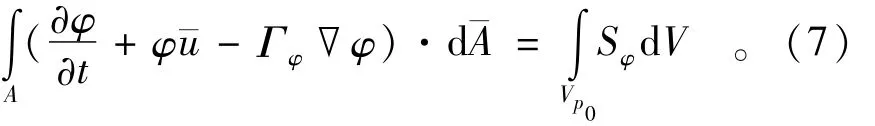
式中:V为控制体的体积(单元面积);A为控制体的表面积(单元边长度);A为控制容积界面的面积矢量(边矢量);其正向与外法线单位矢量一致(图1);u为速度矢量。
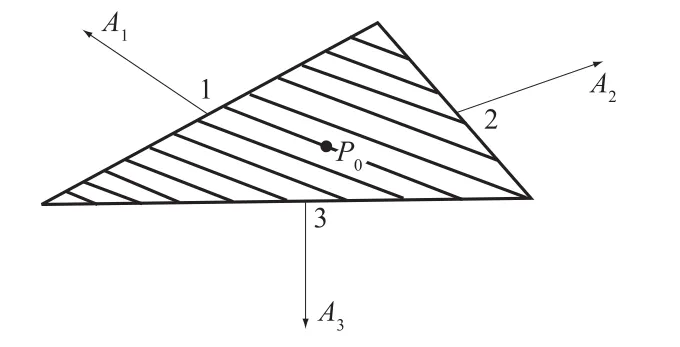
图1 单元矢量布置示意Fig.1 Sketch of unit vector
将式(7)应用与图2所示的控制体,可得

这里,j为控制体中界面(边)的角标。
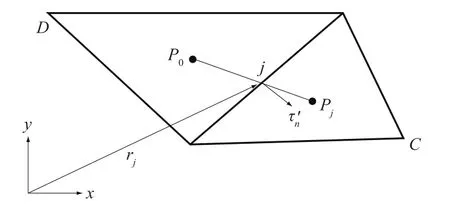
图2 界面上平均值的确定Fig.2 Determ ination of the average value on the interface
当对流项界面插值采用混合方案,混合因子取[0,1]之间值,并采用延迟修正求解;用中心差分计算节点上的梯度;源项采用线性化处理方案时,可得到如下的离散结果

悬沙运动方程(4)的离散与此完全一致,这里就不单独写出其离散表达式。
3.2 离散方程的求解步骤
非结构化同位网格SIMPLE算法的计算步骤如下:
(1)给定初始速度场和水位(压力)场;
(2)由给定的速度场和水位场计算离散动量方程组的系数和源项;
(3)求解动量方程组,得出速度场;
(4)计算水位校正方程中的系数和源项;(5)求解水位校正方程,得到校止水位;(6)修正水位和速度,获得本层次上满足连续方程的速度和水位场;
(7)反复迭代,直至收敛。
由以上可见,在非结构化网格上实施SIMPLE算法的步骤与结构化网格上一致,只不过各个步骤的具体实施方式有较大差别。另外,所有公式及说明都是对速度矢量而言的,实际计算时还需要分别对其直角坐标的分量一一进行。
4 模型在荆江分洪区的应用
荆江分洪区位于荆江南岸,是荆江地区防洪系统的主要组成部分,分洪区面积921 km2,1995年全区共有人口48.25万,有效蓄洪容量54亿m3。荆江分洪工程包括进洪闸、节制闸和分洪区围堤。进洪闸位于太平口东岸,设计进洪流量8 000 m3/s。
荆江河段的安全泄量约为68 000 m3/s(包括向洞庭湖分流),其中沙市河段只能通过50 000 m3/s。超过这个标准,则需要考虑运用荆江分洪区。荆江分蓄洪区的主要功能在于分泄荆江河段的超承洪水流量,降低荆江的洪水位,使洪水能够安全通过,而不致超过荆江大堤的防御能力,以确保荆江两岸广大农田和人民生命财产安全。同时由于分洪后荆江水位降低,四口分泄入湖的流量减少,并且由于荆江下泄量减少,岳阳出湖流量也可能相对增加,因而也就间接地减轻了洞庭湖的负担,在1954年的洪水情况下,这项工程曾发挥了“江湖两利”的重大作用。
采用以上建立的模型,对1954年荆江分洪区分洪过程进行了复演计算。
4.1 模型的建立及相关问题处理
4.1.1 基于DEM模型的地形自动剖分技术
计算网格地形根据美国SRTM 90 m DEM数字模型插值得到。计算区域为整个荆江分蓄洪区,以北闸为进流边界,南闸为出流边界,分蓄洪区的围堤为其不过水边界。计算网格采用三角网格,节点总数2 964个,单元总数5 614个,最长边长1 396 m,最短边长119 m,如图3所示。

图3 荆江分洪区网格划分Fig.3 Grid partition of Jingjiang flood-division area
4.1.2 动边界模拟
溃坝水流计算关键在于如何进行干河床与动边界的处理。笔者在前人研究基础上,提出了能适应溃坝水流动边界的处理方法[6]。其主要思路是:首先给定一很小水深hmin,根据计算得到的节点水深来判断节点的“干湿”情况,当h>hmin时为湿节点;否则为干节点,并令干节点h=hmin。对于干节点,还需根据相邻节点水位来判断是否进行“冻结”处理,若其周围均为干节点,或其周围有湿节点但其水位低于该干节点河床高程时,则对该干节点进行冻结处理,即糙率取为极大值(如1010);否则“不冻结”,节点糙率为正常值。
4.1.3 参系数取值
由于荆江分蓄洪区内缺乏实测的洪水资料,因此,糙率参考相关资料确定:树林0.070,旱地0.065,水田0.050,水面0.025。如果某网格内含有多种地形,则按照各种地形糙率的加权平均值确定该网格的糙率。此外,经验表明,糙率随水深增加而减小,并趋于稳定,据此规律确定洪水演进计算中网格节点的糙率。
紊动粘性系数采用υt=αu*h公式计算,α为常数,取为0.5,u*为摩阻流速。
4.2 计算条件
1954年洪水具有流量大、历时长的特点,荆江工程曾先后3次开闸运用:第1次分洪从7月22日2时20分至27日13时10分,分洪总量达23.5亿m3;第2次分洪从7月29日6时15分至8月1日15时55分,分洪量约17.2亿m3;第3次分洪从8月1日21时40分至22日7时50分,分洪量约81.9亿m3(包括腊林洲扒口分洪在内)。以上3次分洪总量为122.6亿m3(8月22日7时50分以后开闸及腊林洲扒口流量未计在内)。
模拟计算时假定闸门瞬间开启,忽略闸门的开启过程。闸门上游水位保持不变直至蓄满为止。
4.3 洪水演进计算成果分析
计算结果表明,分洪闸下泄流量先缓慢增大,后快速减小,最大下泄流量可达8 000 m3/s,分洪区蓄满所需时间为11 d左右,分洪量约为60亿m3。
图4给出了荆江分蓄洪区分洪后3 h和24 h时流速矢量和淹没水深套绘图,由图中可见在缩窄部位流速增大,水流首先占据低洼部位,然后水位逐步抬升。
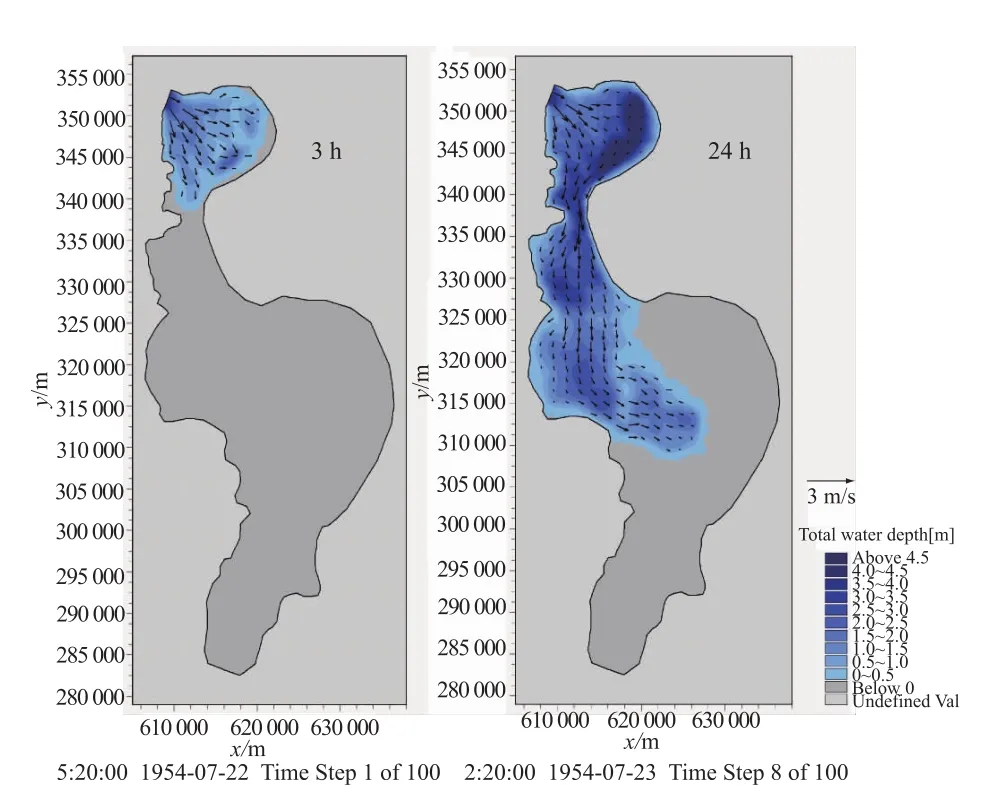
图4 不同时刻流速与水深套绘图Fig.4 Flow velocity and water depth at different times
图5 为各采样点流速过程线图。由图可见,在整个分洪过程中,溃口处的P1采样点流速呈逐渐减少趋势,其它采样点流速在分洪初期增大,后随着水位的抬高流速逐渐减少,最大流速为1.2 m/s。同一时刻,离溃口越近的采样点流速一般越大。
4.4 泥沙冲淤计算成果分析
图6为各采样点冲淤幅度过程线(图中负值表示冲刷)。由于P1采样点位于分洪口门附近,故此处河床处于强烈冲刷状态,冲刷初期含沙量最大,为2.0 kg/m3,冲刷深度在分洪后3h内增加最快,最大冲深为1.8 m;P2采样点位于分蓄洪区内束窄段的进口处,流速较大,除了初期略有淤积外,其它时间河床一直处于冲刷状态,其最大冲刷深度为1.2 m;采样点P3和P4由于距离分洪口门较远,大部分泥沙在其前面河床已经落淤,因此这些位置河床淤积幅度很小。

图5 各采样点流速过程线Fig.5 Velocity process curves at each monitoring point
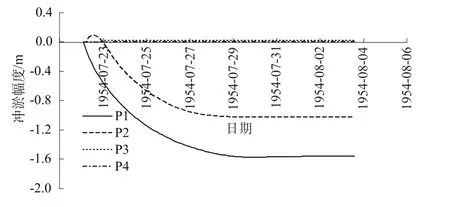
图6 各采样点冲淤幅度过程线Fig.6 Erosion and deposition height process curves at each monitoring point
5 结 论
(1)本文建立的分蓄洪区水沙演进数学模型采用了无结构网格,能很好适应分蓄洪区复杂的边界条件;应用DEM数字模型插值技术,能快速获取计算域的地形高程;模型可同时模拟干河床的洪水演进和河床的冲淤变形。
(2)模型在荆江分洪区得到初步应用,复演了1954年分洪过程,得到主要成果为:最大分洪流量约为8 000 m3/s,蓄满时分洪量约为60亿m3,所需时间为11 d左右;分洪闸后最大流速、含沙量和冲深分别为1.2 m/s、2.0 kg/m3和1.8 m。计算结果表明模型能适应荆江分洪区复杂的地形边界条件,模拟效果较好,成果可为分蓄洪区洪水调度及防洪抢险提供参考。
[1] 余明辉,张小峰.平面二维溃堤水流泥沙数值模拟[J].水科学进展,2001,12(3):286-290.(YU Ming-hui,ZHANG Xiao-feng.Horizontal 2-D Uneven Sedi-mentMathematicalModel in Dike Burst[J].Advances in Water Science,2001,12(3):286-290.(in Chinese))
[2] 王嘉松,何友生.浅水流动与污染物扩散的高分辨率计算模型[J].应用数学和力学,2002,23(7):661-666.(WANG Jia-song,HE You-sheng.High-Resolution Numerical Model for Shallow Water Flows and Pollutant Diffusions[J].Applied Mathematics and Mechanics,2002,23(7):661-666.(in Chinese))
[3] 王志刚,汪德爟,赖锡军,等.下游为干河床的溃坝水流数值模拟[J].水利水运工程学报,2003,(2):18-23.(WANG Zhi-gang,WANG De-guan,LAIXi-jun,et al.Numerical Simulation of Dam-Break Current Flowing in Dry Bed[J].Hydro-science and Engineering,2003,(2):18-23.(in Chinese))
[4] Macchione F,Morelli M A.Practical Aspects in Compa- ring Shock-Capturing Schemes for Dam-break Problems[J].J.Hydraul.Eng.,2002,129:187-195.
[5] 张细兵.河道有限元网格自动剖分方法研究[J].长江科学院院报,2002,(3):19-21.(ZHANG Xi-bing.Au-to-Generating Method of Triangulation Grids for River Reach[J].Journal of Yangtze River Scientific Research Institute,2002,(3):19-21.(in Chinese))
[6] 张细兵,范北林.溃坝洪水演进平面二维数学模型初步研究[J].长江科学院院报,2006,(6):19-21.(ZHANG Xi-bing,FAN Bei-lin.Numerical Simulation for Two-Dimensional Dam-Break Flood Flow[J].Journal of Yangtze River Scientific Research Institute,2006,(6):19-21.(in Chinese) )
(编辑:周晓雁)
Unstructured Grid M odel of Flow and Sediment Evolution in Flood Diversion and Storage Area
ZHANG Xi-bing1,2,OU Zhi-hua3,CUIZhan-feng1,SUN Xian1
(1.River Research Institute,Yangtze River Scientific Research Institute,Wuhan 430010 China;2.College ofWater Resources and Hydroelectric Engineering,Wuhan University,Wuhan 430072 China;3.Honghu Sub-bureau,Jingzhou River Management Bureau of Yangtze River,Honghu 433200 China)
Based on unstructured triangular grid and Finite Volume Method,a flow and sedimentevolutionmodel in flood diversion and storage area is founded in this paper.One advantage is that themodel grids can adapt to compli-cated boundary conditions well,and the terrain data of the computational domain are obtained quickly by using DEM numericalmodel interpolation technology.Another advantage is that the sediment transport and riverbed de-formation can be simulated synchronously.Key techniques including grid partition,numerical separation,treat-ments ofmovable boundary and dry riverbed are studied and the corresponding processingmethods are introduced.Furthermore,themodel has been applied successfully to the simulation of flood diversion in 1954 in Jingjiang flood diversion and storage area.The calculated flood results can serve as reference for flood control policy-making and flood rescue,and themaximum erosion depth behind the flood diversion gate can provide reference for engineering design.
unstructured grid;flood diversion and storage area;flood evolution;sediment erosion and deposition;nu- merical simulation
TV143
A
1001-5485(2011)04-0075-05
2011-02-17
水利部公益性行业专项经费项目(200901003);公益院所基金项目(CKSF2011001)
张细兵(1976-),湖北鄂州人,高级工程师,博士研究生,主要从事河流数值模拟研究,(电话)027-82829871(电子信箱)jss9871@vip.163.com。

