弹性固支平板钢闸门主梁的可靠度分析

王 羿，王正中，，孙丹霞，赵延风

弹性固支平板钢闸门主梁的可靠度分析

王 羿1，王正中1，2，孙丹霞3，赵延风2

（1．西北农林科技大学水利与工程建筑学院，陕西杨凌 712100；2．西北农林科技大学水工程安全与病害防治研究中心，陕西杨凌 712100；3．中国水电顾问集团西北勘测设计研究院，西安 710065）

针对目前平板钢闸门结构形式存在的内力分布不均，主梁跨中弯矩大的问题，根据超静定结构承载力高于静定结构的原理，提出了弹性固定支座平板钢闸门主梁新型结构形式。以跨中截面与支座截面等安全度为原则，确定弹性固定支座截面合理转角；根据结构可靠度理论评价该结构主梁的可靠度指标，并与现行结构形式主梁的可靠度进行比较。结果表明：该新型结构可以在主梁截面不变情况下提高可靠度指标1．44，在可靠度指标不变情况下减少材料30%，可靠度沿跨长的分布均匀，为一种经济合理、安全可靠的结构形式。

平板钢闸门；主梁；弹性固支；合理转角；可靠度分析

1 问题提出

目前，工程中所用的平板钢闸门的结构形式多为两侧门槽对闸门仅提供铰支约束，无法限制主梁端截面（边梁）转角，主梁的力学模型是简支梁，造成跨中弯矩较大，而支座处弯矩为零，内力分布极不均匀，材料强度不能充分发挥，工程上通过变截面和局部加固等方法解决。在结构力学中，将简支梁支座处加上约束弯矩后，可以使跨中弯矩变小，并使梁内弯矩分布较为均匀，如图1所示（其中L为梁跨度）。如果将闸门主梁支座处的简支结构改为固定端支座成为3次超静定结构，工程上难以实现，从定性的角度看，支座处的负弯矩和剪力产生的折算应力将会显著增大，使内力分布及应力分布也不均匀，支座的安全性最低，这是得不偿失的。本文给出2种新的闸门门槽及主梁形式。第1种如图2（a），即梁在端部变高，铰支固定于门槽上，支座处的滚轮既可以起到限制主梁端截面转角位移，又可以代替侧轮的作用，起到增加约束的作用。第2种如图2（b），在上、下翼缘处加约束，上翼缘的行走支承受拉，下翼缘行走支承受压。允许主梁支座截面发生一个合理的角位移，以便跨中截面与梁端截面达到相同安全度的目的。这样既能减少支座的弯矩值，使得折算应力减小，并且弹性固定支座也较容易在实际工程中实现。以跨中截面与梁端截面达到相同安全度为原则，以结构承载力最大为目标，进行定量的计算以确定合理的角位移量及相应的结构可靠度指标。

图1 不同支座约束的梁弯矩图Fig．1 Bendingmoment diagrams of girder of different constraint bearing

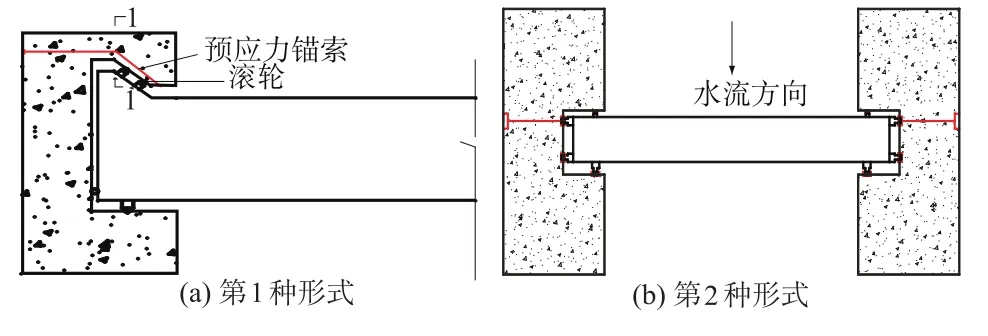
图2 弹性支座梁Fig．2 Beam on elastic bearing

为防止门槽1-1截面处拉裂，可以参照文献［1］，［2］的弧形钢闸门支墩预应力锚索技术，在门槽内侧埋置预应力锚索预加压力形成偏心受压，且受压面在内侧。实践证明，预应力锚索技术能确保深孔弧形闸门受集中力作用时2个支墩安全可靠，同理采用预应力锚索技术，能保证分布荷载作用下的门槽安全，并避免内侧拉裂，因此，这种门槽是安全可行的。该门槽向主梁施加的约束为弹性的，只允许主梁支座微小变形。与简支约束不能限制支座变形相比，其正常工作的可靠性更高。

2 内力计算

根据结构力学方法求解超静定结构内力，计算简图为超静定结构，又因为对称，所以基本结构取一半，如图3。

图3 弹性固定梁半边结构计算简图Fig．3 The internal force calculation diagram of half-structure of the beam fixed by elastic bearing

力法方程为

由图乘法解得

支座处

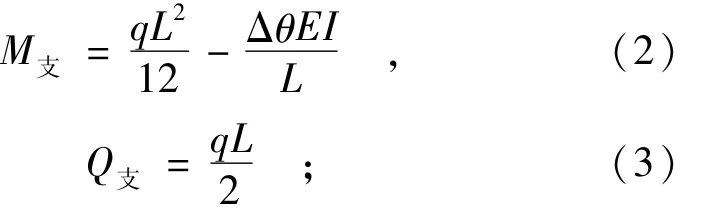
跨中

式中：X1为未知弯矩；δ11为X1＝1作用时基本体系支座处位移（rad）；Δ1p为单独荷载作用时基本体系支座位移（rad）；M支为支座弯矩（N·m）；Q支为支座剪力（N）；M中为跨中弯矩，（N·m）；Δθ为弹性支座合理转角（rad）；E为材料弹性模量（MPa）；I为截面惯性矩（m4）；q为均布荷载（kN／m）；L为梁跨度（m）。

上式为通式，当Δθ＝0时，为两端固支情况下的内力；当Δθ＝ql3／（12EI）时，为简支情况下的内力。

3 应力计算

为计算方便，以沿跨度等截面梁为例进行计算，如图3，典型断面如图4。b1，b2，h0，t0，t1，tw分别为上翼缘宽度、下翼缘宽度、腹板高度、上下翼缘厚度、面板厚度和腹板厚度。

式中：M为截面弯矩（N·m）；Q为剪力（N）；σ为截面弯曲正应力（MPa）；τ为剪应力（MPa）；σzh为弯剪折算应力（MPa）；I0为截面中性轴惯性矩；Wmin为下翼缘底部抗弯截面模量为验算点面积距。

图4 主梁典型截面图Fig．4 Typical section of themain girder

将跨中弯矩、支座负弯矩、支座剪力分别代入式（5）、式（6），得跨中弯曲正应力（σ1）、支座弯曲正应力和剪应力；再将翼缘和腹板相接处的正应力和剪应力代入（7）式求得支座处折算应力（σzh）。

4 弹性固定支座合理转角的确定

弹性固定支座合理转角的确定原则为在荷载作用下跨中和支座同时破坏。先确定跨中和支座处的控制应力，再令二者相等求得合理转角。

4．1 控制应力

因跨中只有弯曲正应力，故控制应力为正应力σ1。

支座处应力有弯曲正应力、剪应力和弯剪复合应力；经分析表明：非双轴对称工字型梁下翼缘正应力，腹板最大应力，下翼缘与腹板相接处正应力及剪应力的复合应力三者中复合应力为最大控制应力，

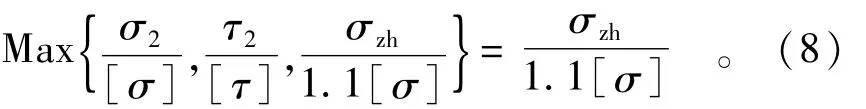
4．2 合理转角

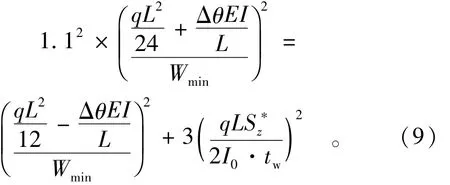
由于Δθ很小，故略去二阶微量Δθ2项得

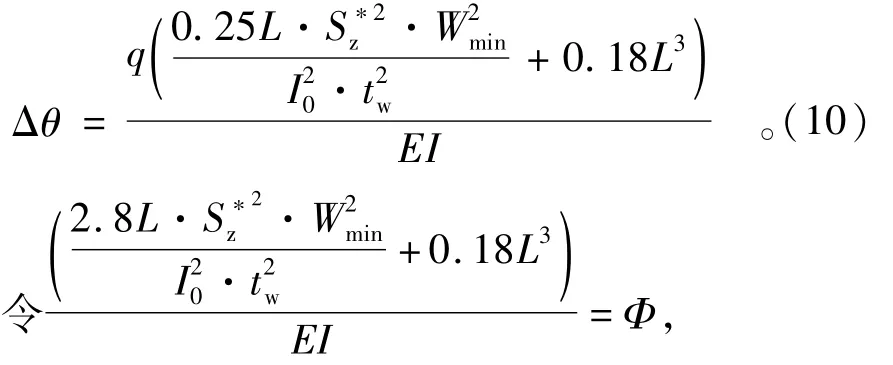
合理转角为

利用式（11）计算的Δθ为理论最合理转角，在实际中可以使合理转角为一个范围，即令其中δ表示跨中与支座的可靠度相差的程度，根据工程需要取值。

5 可靠度分析

5．1 功能函数与计算公式的确定

根据文献［4］闸门简支主梁破坏形式有3种，分别是主梁弯曲破坏、剪切破坏及弯剪复合破坏。对于本文的弹性固定支座梁，根据以上分析，在支座处剪切破坏，弯曲破坏不起控制作用，而弯剪复合破坏是控制状态；在跨中处剪切破坏，弯剪复合破坏不起控制作用，而弯曲破坏是控制状态。功能函数为：

跨中弯曲破坏

支座复合破坏

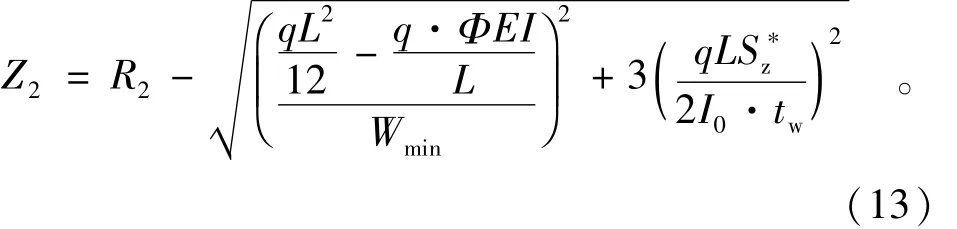
因为R2＝1．1R1，将式（12）、（13）化为同水平比较

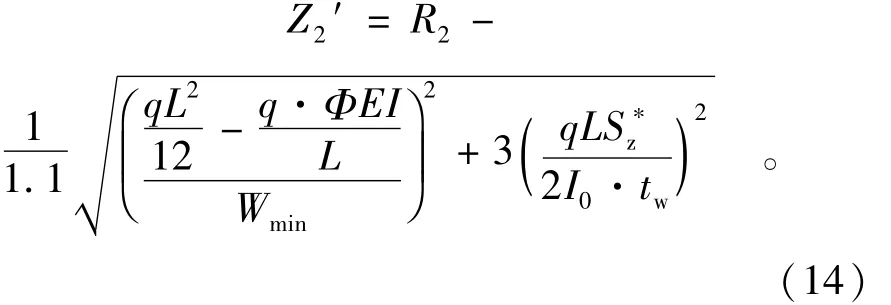
对Z1，Z2荷载函数S1，S2中随机变量只有q，故

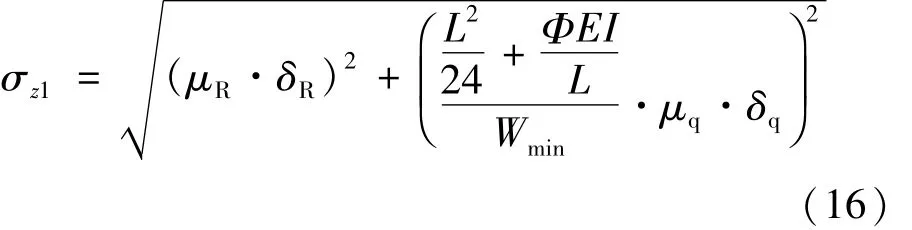
Z2原函数为非线性，对其进行泰勒级数展开变为线性，在均值点处泰勒展开为线性函数，对其求均值与标准差

故：

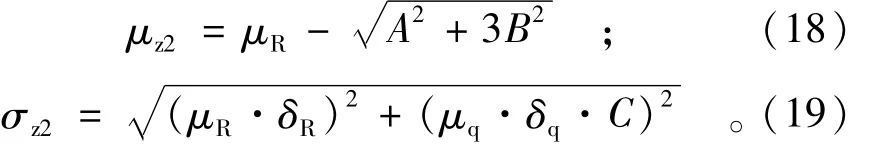
式中：μR为抗力均值（MPa）；μq为荷载均值（kN／m）；R1，R2为跨中截面和支座截面材料抗力（MPa）；σR为抗力标准差（MPa）；σq为荷载标准差（kN／m）。

5．2 荷载分析

主梁可靠度指标只与其偏差系数和变异系数有关。本文以文献［5］中的主梁为例进行分析，该闸门主梁的跨中截面如图3所示，表1为各变量及跨度L、参数γ的设计值、偏差系数和变异系数，表中α为主梁支承端截面腹板高度折减系数，L为跨度，γ为截面高度改变处至跨中距离与主梁跨度L的比值，q为主梁分布荷载。b1，b2，h0和L的变异系数小于0．01，视为确定量，并且为计算简便，将t0，tw，t1也按确定量计算。本文对在计算弹性固定支座主梁时取等截面，所以对表1的数据如α和γ并不采用。采用截尾正态分布，避免概率分布函数尾部对可靠指标的影响［5］。

5．3 抗力分析

主梁抗力只包含材料性能和计算模式的不确定性［4］，其表达式如下：

式中：Rn为抗力标准值；M为材料性能的不确定性统计参数；P为抗力计算模式的不确定性统计参数。

材料性能的统计参数可取钢结构设计规范校准时的参数［6］。钢闸门主梁在荷载的作用下，受弯和受剪破坏计算模式不确定性的统计参数，取钢结构设计规范校准时的参数；对于弯剪复合破坏来说，将其计算模式不确定性近似按受弯破坏来考虑，这是因为剪力对弯曲正应力的影响很小［7］。根据式（16）可得3种失效模式下抗力的统计参数［5］，结果见表2。此外，由文献［4］，［5］可知，钢闸门抗力一般为对数正态分布。

表1 荷载基本变量的统计参数Table 1 Statistical parameters of load variable

表2 主梁抗力偏差系数与变异系数Table 2 Deviation coefficients and variation coefficients ofmain beam’s resistance

5．4 可靠度指标计算

根据表1与表2数据，以Q235钢为例计算。已知在由简支结构变为弹性支座后梁跨中弯矩必减小，在截面不变的情况下可靠度指标必增大，不必再验证，而只须比较变化前后支座处可靠度指标的变化。计算结果如下：

当Δθ＝0．003 8弧度时（为简支梁控制转角的0．5），弹性梁支座与跨中同时破坏，此时2种情况下可靠度指标如表3所示，此外为了更加突出弹性固定梁优势，本文令2种梁可靠度相等求得弹性固定支座梁只需0．7 m，并在表3给出了其跨中与支座可靠度指标。

简支主梁在跨中和支座处可靠度指标不同，这时因为文献［5］仅在支座附近降低梁高却没有加厚腹板厚度，其选取的主梁截面是不科学的，实际支座可靠度指标也应达到4．01左右，经计算需要加厚腹板为1．2 cm。这也说明简支梁在设计时很复杂，而采用弹性固定支座主梁按等截面设计，非常简单。

表3 计算结果Table 3 Calculation results

下面比较原简支梁与采用弹性固定支座并降低梁高为0．7 m后的主梁沿梁跨长可靠度和钢材用量，由于主梁关于跨中对称，以左支座为坐标原点绘左半跨，结果如图5。

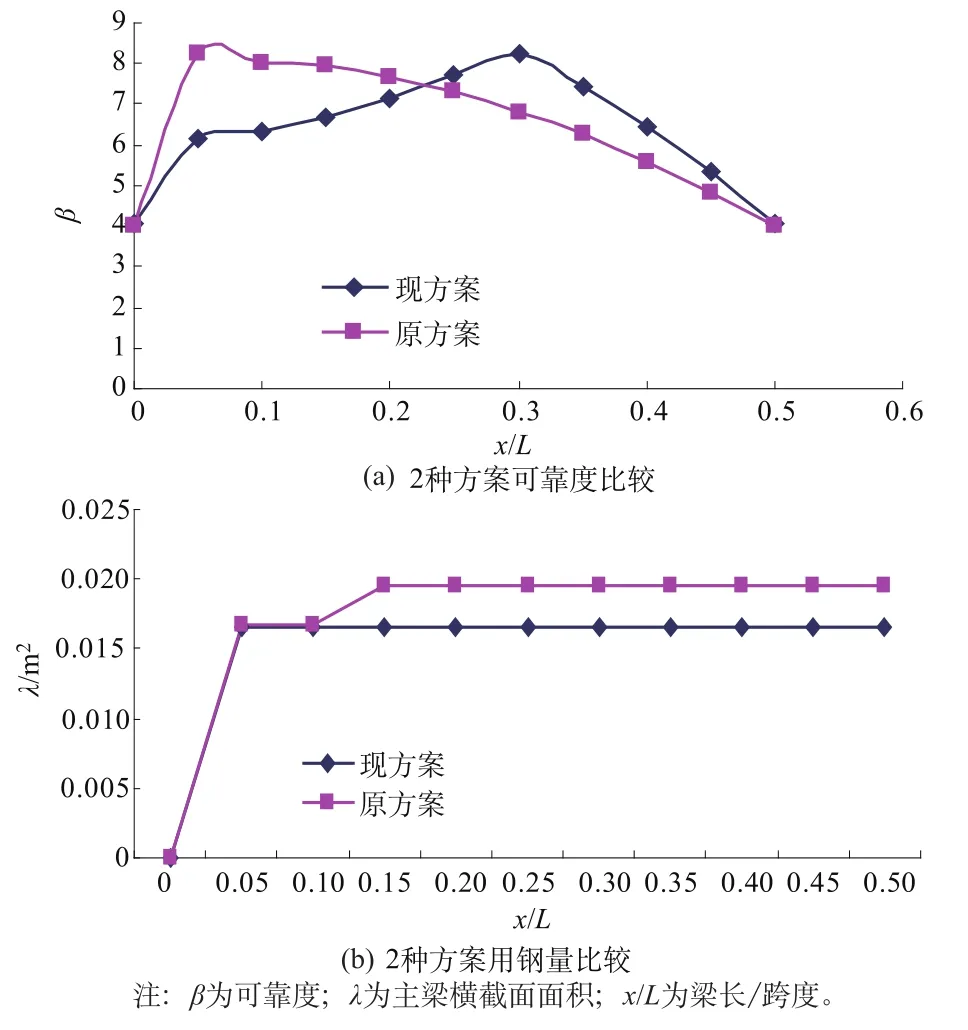
图5 可靠度和截面面积沿梁跨长分布图Fig．5 Scattergram of reliability and cross sectional area along span length

由图5可以看出，在保持与原结构相同可靠度的前提下，本文提出方案不仅节省材料接近30%，同时横向隔板材料用量也有相应的减少；而且主梁便于焊接。表明降低梁高并采用等截面设计的弹性固定梁沿梁长的可靠度分布和钢材用量都优于原先的简支梁。

6 结 论

（1）通过以上计算证明改变梁两端的约束形式确实可以提高结构的安全性，而且应力分布也比较均匀，就本文例题而言可靠度指标提高了1．44；或者在可靠度不变的情况下，将闸门主梁变为弹性支座可以减小断面，从而节省钢材减轻闸门自重，降低安装难度，就本文例题而言钢材节省近30%。

（2）根据本文给出的允许转角Δθ的计算公式可以确定，允许转角Δθ在理论合理值附近一个范围内变化而不会显著降低可靠度。

（3）结构的超静定次数和约束的位置对结构可靠度影响较大，这应该在极限状态设计的功能函数中体现，建立这样的功能函数可以使基于可靠度的结构设计的优化具有更加量化的手段。本文进行这种功能函数关系的探索，可以看出结构的超静定次数和约束形式是通过荷载函数中的Δθ来影响可靠度的。

（4）支座处增加约束成为超静定后，对结构的改变表现在门槽节点处增加弯应力，与原先的剪应力叠加产生折算应力，使该点的受力状态变得复杂。经过可靠度指标的计算并参考工程实际中对门槽的预应力处理技术，可以保证该点的安全可靠性满足要求。

［1］ 范崇仁．水工钢结构设计［M］．北京：中国水利水电出版社，1990．（FAN Chong-ren．Hydraulic Steel Structure Design［M］．Bejing：China Water Power Press，1990．（in Chinese））

［2］ 贺采旭，李传才，何亚伯．大推力预应力闸墩的设计方法［J］．水利水电技术，1997，31（6）：24－29．（HE Cai-xu，LIChuan-cai，HE Ya-bo．Study on the Design Meth-od of Prestressed Concrete Sluice Bearing Large Pressure［J］．Water Resources and Hydropower Engineering，1997，31（6）：24－29．（in Chinese））

［3］ 王正中，赵延风．刘家峡水电站深孔弧门按双向平面主框架分析计算的探讨［J］．水力发电，1992，（7）：41－44．（WANG Zheng-zhong，ZHAO Yan-feng．Dis-cuss on Analysis and Calculation of Deep-Hole Radial Gate by Bidirectional Plane Main Frame in Liujiaxia Hy-dropower Station［J］．Water Power，1992，（7）：41－44．（in Chinese））

［4］ 李宗利．平面钢闸门主梁可靠度校准分析［J］．水力发电，1998，（2）：52－57．（LIZong-li．Analysis on the Re-liability Standard of Primary Beam of Plane Steel Gate［J］．Water Power，1998，（2）：52－57．（in Chinese））

［5］ 李典庆，吴帅兵．水工平面钢闸门主梁多失效模式相关的系统可靠度分析［J］．水利学报，2009，（7）：870－877．（LIDian-qing，WU Shuai-bing．System Reli-ability Analysis on Main Girder of Plane Gates Consider-ing Multiple Correlated Failure Modes［J］．Journal of Hy-draulic Engineering，2009，（7）：870－877．（in Chi-nese））

［6］ 李典庆，张圣坤．平面钢闸门主梁可靠度评估［J］．中国农村水利水电，2003，（3）：19－22．（LI Dian-qing，ZHANG Sheng-kun．Reliability Assessmentof Plane Steel Gate Main Beam［J］．China RuralWater and Hydropow-er，2003，（3）：19－22．（in Chinese））

［7］ 王正中，沙际德．深孔钢闸门主梁横力穹曲正应力与挠度计算［J］．水利学报，1995，（9）：40－46．（WANG Zheng-zhong，SHA Ji-de．Calculation of Normal Stress and Deflection in Transverse Bending of Main Beam in OutletGate［J］．Journalof Hydraulic Engineering，1995，（9）：40－46．（in Chinese））

［8］ ISO2394—1998，General Principles of Reliability for Structures［S］．

［9］ 曹双寅，舒赣平．工程结构设计原理［M］．南京：东南大学出版社，2002．（CAO Shuang-yin，SHU Gan-ping．Engineering Structural Design Principle［M］．Nanjing：Southeast University Press，2002．（in Chinese））

［10］解 伟，李昆良．水工结构可靠度设计［M］．郑州：河南科学技术出版社，1997．（XIE Wei，LI Kun-liang．Hydraulic Structure Reliability Design［M］．Zhengzhou：Henan Science and Technology Press，1997．（in Chi- nese） ）

（编辑：刘运飞）

M ain Girder Reliability of Plane Gate Fixed by Elastic Bearing

WANG Yi1，WANG Zheng-zhong1，2，SUN Dan-xia3，ZHAO Yan-feng2
（1．College ofWater Conservancy and Architectural Engineering，Northwest Sci-tech University of Agriculture and Forestry，Yangling，Shaanxi 712100，China；2．Research Center ofWater Engineering Safety and Disaster Prevention，Northwest A＆F University，Yangling Shaanxi 712100，China；3．Hydrochina Xibei Engineering Corporation，Xi’an Shaanxi 710065，China）

To solve the problems in current plane gate structures such as uneven distribution of internal forces and large bendingmoment inmain girdermid-span，a new main girder structure of plane steel gate fixed by elastic bear-ing is proposed according to the theory that the bearing capacity of statically indeterminate structure is higher than

that of statically determinate structure．Taking the equal safety degree betweenmid-span section and bearing section as a principle，the reasonable corner of the elastic fixed bearing section is determined；and based on structural reli-ability theory，the reliability index of the main girder is evaluated and is compared with the reliability of existing structure girder．The results show that the new structure can improve the reliability index by 1．44 under a constant main beam section；or reduce thematerial consumption by 30%under a constant reliability index；and the distribu-tion of reliability along the span length is uniform．Therefore，it is an economical，safe and reliable structure．

plane steel gate，main girder，elastic fixed bearing，reasonable corner，reliability analysis

TV131．4

A

1001－5485（2011）04－0054－05

2010-04-15

国家“863”高技术研究与发展计划项目（2002AA62Z3191）；陕西省水利科技专项计划项目（2006－01）

王 羿（1987-），男，山西长治人，本科生，主要从事农业水利工程专业，（电话）15991774721（电子信箱）wangyimutou＠126．com。

王正中（1963-），男，陕西郴县人，教授，博士生导师，从事水工水力学研究，（电话）13319210121（电子信箱）wangzz0910＠yahoo．com．cn。