SIFT算法图像自适应优化
汪丽华,汪道寅,王泽梁
(1.黄山学院信息工程学院,安徽 黄山245041;2.中国科学技术大学电子工程与信息科学系,安徽 合肥,230027;3.合肥工业大学计算机与信息学院,安徽合肥230009)
0 引言
尺度不变特征变换(Scale-Invariant Feature Transform,SIFT)算法具有尺度、旋转、仿射和光照等不变性的特征[1]。该算法主要包含两个阶段:一是SIFT特征生成,即从待配准图像中提取对尺度缩放、旋转、亮度变化无关的特征向量;二是SIFT特征向量的匹配。通过对比SIFT,PCA-SIFT,steerable filter,moment invariants等数10种特征描述后指出[2],SIFT是目前最为有效地特征检测算子。SIFT算法因其性能的优异,得到广泛关注,陆续出现了一些变种算法,PCA-SIFT 算法[3]、GLOH 算法[2]、SURF 算法[4]、ASIFT算法[5]等。本文通过对SIFT算法配准过程进行研究,针对其未根据图像调整配准区间的不足实现了图像自适应的配准区间参数优化方法,实验表明优化更有效的实现了图像配准。
1 SIFT算法简介
二维图像在计算机中可以表示为二维灰度矩阵,从不同的距离观察同一场景则得到该场景的不同尺度下的图像,构成了图像金字塔,即该场景的尺度空间表示。
1.1 图像特征点确定
图像金字塔可以用图像和可变高斯核函数的卷积表示。Lowe利用归一化拉普拉斯近似,对图像金字塔相邻层求差,构造出差分高斯金字塔,其表示如下:
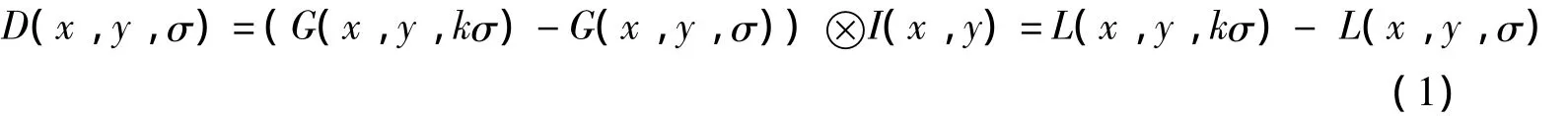
用梯度方向直方图来统计邻域象素的梯度方向。在0~360°的梯度方向中,每10°表示为一个柱,直方图的峰值便是该特征点主方向。
1.2 特征描述符形成
在以特征点为中心的16×16的象素区域中(不含特征点所在行、列),利用高斯加权法统计每个4×4的小块的8个方向的梯度方向直方图的累加值,构成16×16/4×4=16个种子点。特征描述符由所有小块的梯度方向直方图构成。因此,最终形成8×16=128维的SIFT特征向量。
1.3 特征点匹配
当最近邻和次近邻之间的欧氏距离的比值|DA-DB|/|DA-DC|满足一定区间范围要求时,此时的最近邻欧氏距离所对应的特征点是匹配特征点。因此可通过计算特征描述符之间的欧氏距离大小来确定2个特征点的匹配度。当2个特征描述符的欧氏距离最小且与次最小欧氏距离的比值属于区间[0,0.8],则这2个特征点为匹配点。
2 算法优化思路
Lowe根据大量图像统计的欧氏距离比概率密度分布[1]将距离比区间固定为[0,0.8],此方法未必恰当,因其不能体现具体图像的欧氏距离比概率密度分布。具体图像匹配时,该区间并不总能适应。为使区间参数具有尽可能高的适应性以满足不同情况需要,该区间参数应能根据图像自适应调整。
对于同一场景的两幅图像,定义其中都出现的特征点占所有特征点的比例为重复率,重复率反映了整个算法检测到的特征点的几何稳定性,它可以作为图像配准算法评价的一个标准。通过在算法中加入自适应过程来找到与具体图像相适应的欧氏距离比区间参数,用重复率来衡量参数是否已适应。重复率大,则表明匹配程度高,区间选取合理;反之则区间选取越不合理。目前尚无研究成果表明重复率与欧氏距离比区间设定的关系,通过大量实验,得出欧氏距离比区间上界在[0.4,0.8]之间较为恰当。匹配区间上界太大,则要求太宽泛,错配点将增多;匹配区间上界太小,则要求太严,正配点将减少。目前已有很多智能优化方法,如遗传算法、蚁群算法等。由于仅需对欧氏距离比区间参数在已明确的大致范围内进行调整,为减少不必要的时间消耗可不采用上述智能方法。从欧氏距离比概率密度分布曲线可知,正配点的概率密度在距离比0.45左右时达到极值,而后开始减小,因而距离比设定在前端的可能性更大些,故按照斐波那契数列将区间分块,块内随机摆动探测。具体思路为:(1)设待找寻区间为[l,h],以斐波那契数列前n项为长度将区间划分为n块;(2)在每块中随机产生一点c1~cn,计算其重复率R(ci);(3)令nm=max(R(ci)),选取nm所在的区间作为新的待找寻区间,划分为n块,重复步骤(2)直至前后两次的nm相差小于0.01或找寻次数大于50或nm=1。
较之于二分查找的方法,斐波那契分块充分考虑了正配点在距离比设定变化时的概率密度分布趋势,在正配点高密度处查找更多,同时一次划分更多块,整个算法循环次数减少。由于匹配环节占SIFT算法中的整个运算比例很小,故以上过程不会给SIFT算法带来太大的运算负担。
3 实验结果及分析
3.1 实验图像
实验以湖边教学楼图像为例,如图1所示,图1(a)为大小131×131的参考图像,图1(b)为图1(a)逆时针旋转30°后形成的大小为179×179的待配准图像。
3.2 特征产生与表示
参考图像共检测到148个特征点,待配准图像共检测到164个特征点,检测结果如图2所示。对检测到的特征点生成特征描述算子时,描述子的位置和特征点的位置一致。

图1 参考图像和待配准图像

图2 参考图像和待配准图像的特征点分布
3.3 距离比区间优化过程
实验中欧氏距离比区间参数寻优过程如图3所示。通过分块查找的算法,距离比区间参数不断寻优,直到最大重复率与相应距离比区间。图1的实验图像的配准算法共进行了15轮分块,重复率取得0.982 6,距离比区间上界取得0.689 2。由图3可以看到,距离比区间参数通过不断分块、摆动、接近并最后取得适合的取值。
距离比区间参数对不同的图像其值的选取是不同的,并且具有不同的分布,所以应该针对不同的图像进行选择。本文图像的距离比区间与重复率的关系如图4所示,可知图像距离比上界设定在0.72后重复率下降,因而其最优距离比上界约为0.72,由此亦论证固定距离比区间上界为0.8是不恰当的。由于算法利用斐波那契数列分块寻优思想,能够较快的找到此最优参数。
4 结束语
因SIFT算法具有尺度、旋转、仿射和光照等不变性等优点,因而普遍应用于各类图像配准领域。本文在该算法的特征匹配阶段分块随机摆动调整距离比区间,通过实验验证,这一优化能在增加可接受的运算量下找到更优的距离比区间,更适应具体图像配准。后续工作将对不同类型的图像进行更多实验和比较以分析距离比范围的取值规律。
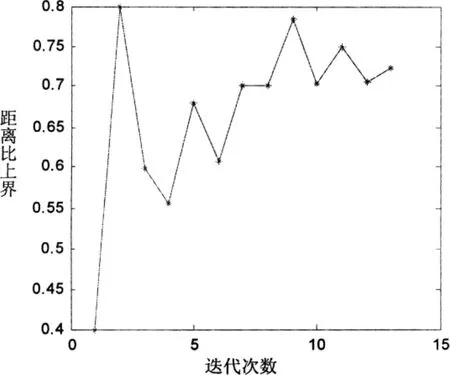
图3 距离比区间迭代过程
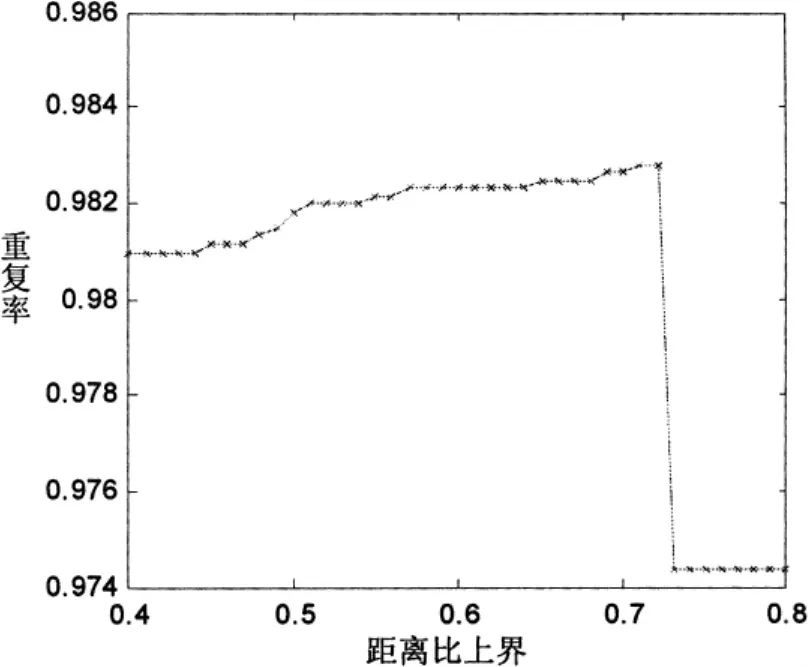
图4 距离比区间与重复率的关系
[1] David L G.Distinctive Image Features from Scale-invariant Keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.
[2] Mikolajczyk k,Schmid C.A Performance Evaluation of Local Descriptors[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(10):1 615-1 630.
[3] Ke Y,Sukthankar R.PCA-SIFT:A more distinctive representation for local image descriptors[C].Washington,DC:Proceedings of IEEE International Conference on Computer Vision and Pattern Recognition,2004:511-517.
[4] Bay H,Tuytelaars T,Gool L V.SURF:Speeded up robust features[C].Berlin:Springer-Verlag,2006:404 -417.
[5] Morel J M,Yu G S.ASIFT:A New Framework for Fully Affine Invariant Image Comparison[J].Society for Industrial and Applied Mathematics Journal on Image Sciences,2009,2(2):438 -469.
[6] Mikolajczyk K,Schmid C.Scale and Affine invariant interest point detectors[J].International Journal of Computer Vision,2004,60(1):63-86.

