颗粒群在平面湍射流中输运弥散的大涡模拟
吴迪冲
(浙江财经学院工商管理学院,浙江杭州310018)
0 引言
射流喷涂技术是机械、化工、纺织、材料工业中一项重要方法。在射流喷涂技术中,涂料悬浮于射流场形成气粒两相流动,颗粒输运及弥散对整个系统的效率有着重要的影响。不少研究者分别用统计方法[1,2]、矩方法[3,4],以及实验方法[5],对其进行研究,取得了一定成果。平面湍射流场作为一个典型的剪切流场,其中的漩涡结构对整个流场及其中的颗粒影响显著,因此不能采用相对简单的雷诺时均方法。另一方面,直接数值模拟,由于对资源的需求过大,也不可作为日常研究而使用。介于上述两者之间,大涡模拟作为一种有效的计算方法,正在被研究学者所广泛采用[6]。从前面的叙述也大概发现,目前学者对颗粒相的研究,也多集中在射流场Re数和颗粒Stk数等几个参数的讨论,而针对不同射流入口颗粒的质量流率的分析,还仅限于实验研究,由于实验研究本身的一些局限性,本文采用大涡模拟的数值方法,拟对这一问题再进行更为全面的讨论和分析。
1 数学模型及控制方程
1.1 流场及大涡模拟
本文的研究对象是如图1所示的射流场及悬浮其中的细小颗粒。x和y定义在流动方向和流动垂直方向,喷嘴宽度D为5mm,喷嘴入口处的进口速度U0=m/s,湍流脉动强度为5%。计算区域是x×y=20D×20D,右端和上下边界可以假定为充分发展的边界条件。对非稳态流场,取每个时间步长Δt=2×10-5s,则无量纲时间 T=t/Δt。
平面射流作为湍流,采用大涡模拟方法,N-S方程经过空间尺度和时间尺度滤波,得到质量和动量方程:
1.2 颗粒轨道方法
对悬浮于气流场中的颗粒离散相,采用拉格朗日观点下的颗粒运动微分方程来求解追踪其轨道。则两个方向(i取1,2)的颗粒作用力平衡微分方程为:

式中,FD(ui-upi)是颗粒单位质量曳力,Fi为对应方向使颗粒周围流体加速而引起的附加质量力。
由于本文数值模拟的颗粒粒径为1 μm,相对于单位质量曳力和附加质量力,其它力可以忽略,但需要考虑颗粒所受曳力的Cunningham修正:

式中,Cunningham 修正因子为 Cc=1+2λ/dp[1.257+0.4exp(-1.1dp/2λ)],其中 λ 为气体分子平均自由程。
2 结果及讨论
2.1 流场涡量分布
流场中的漩涡分布位置及强度大小,可以用速度旋度的绝对值大小来定量体现,对于二维平面流动有:

T=2 000时的流场涡量分布图如图2所示。观察图片可以发现,从喷嘴入口处流入流场的运动气体和原流场中的静止流体在分界层上不断的互相剪切,从而累积涡量到最大值,随着流动的发展,漩涡尺寸不断的增长并脱落。脱落后的漩涡在随流场向下游运动的过程中保持着逐渐增大,到一定尺寸后,与下游的漩涡互相配对、互相影响,共同向下游发展而去,从而形成相对稳定的漩涡分布。

图1 流场及坐标系示意图

图2 T=2 000时的流场涡量图
2.2 颗粒滞留时间
为了分析不同质量流率的粒子群在平面湍射流场中的不同动力学行为,给出了1 μm粒径颗粒在不同质量流率下的浓度及滞留时间分布图,如图3、4所示,其无量纲时间分别为T=1 000,2 000。
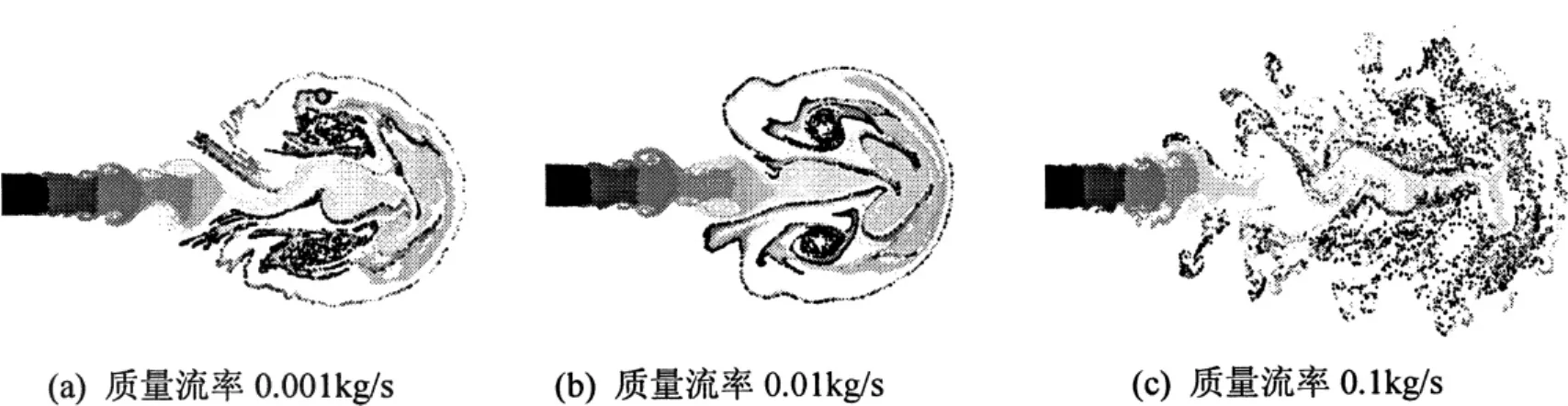
图3 颗粒群在流场中的滞留时间分布图,T=1 000

图4 颗粒群在流场中的滞留时间分布图,T=2 000
观察图3发现,不同质量流率颗粒群在流场中的分布,有相当明显的区别。由于此时T=1 000,流场尚处于发展阶段,漩涡,其尺度和强度都还在持续增加。图3(a)中,当流率在0.001kg/s时,由于粒径较小,颗粒的惯性占据其动力学性能的主导,而且颗粒浓度较低,颗粒间互相影响较小,从而使得颗粒相在流场中的分布,基本和气流场的流场结构相类似。
图3(b)中,当质量流率为0.01kg/s时,其分布模式整体和0.001kg/s的相似,但由于此时颗粒质量流率相对增加了一些,颗粒间的碰撞机会增多,有少部分颗粒从流动区域逃逸到原先静止的流体区域。当颗粒质量流率增加到0.1kg/s时,颗粒的分布基本和流场形态关系不大,在整个射流外围区域,都相对均匀的分布着被漩涡带出或由碰撞反弹出来的颗粒。
图4给出的是不同质量流率在射流场已经基本发展完成时(T=2 000)的颗粒分布及对应的滞留时间分布图。在这里,同样看到了类似于图3的分布模式。在图4(a)、(b)中,流场的后半程区域内,颗粒滞留时间普遍较大,相对的,质量流率为0.001kg/s时,颗粒分布与流场漩涡结构的模式更为相关,而流率在0.01kg/s时,在漩涡结构的边缘处有少量零星分布的颗粒,并且漩涡外围的颗粒分布也相对0.001kg/s流率时有较多毛刺,可见,如果要将颗粒作为流场的示踪粒子的话,0.001kg/s的质量流率是相对比较理想的。图4(c)中,当质量流率为0.1kg/s时,颗粒在流动的中下游阶段射流区域外都有分布,浓度相对均匀,滞留时间也相对均匀。
2.3 流场平均浓度
不同垂直流向(即y方向)位置的颗粒平均浓度折线如图5、6所示,可以看出颗粒从射流中心区域在卷起大涡的作用下向静止流体区域输运的整体趋势。在T=200流场漩涡结构尚处于建立阶段时,图5(a)中,此时射流中心区域的颗粒浓度远大于射流区域以外,并且质量流率越大,颗粒的浓度值越高。如果把颗粒的平均浓度值用入口质量流量进行归一化,图5(b)中,发现不同的质量流率在颗粒平均浓度的整体分布模式上,影响不大。

图5 T=200时颗粒平均浓度分布
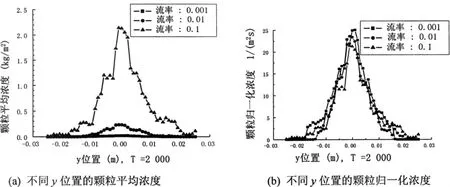
图6 T=2 000时颗粒平均浓度分布
图6 中,当T=2 000,流场充分发展时的颗粒平均浓度,此时流场内不断产生并发展的漩涡和不断互相配对、影响至破碎的小漩涡同时存在,射流对颗粒的搅混作用愈加显著。此时的颗粒浓度最大值依旧在射流中心区域,但从中心区域到射流外围区域的浓度变化相对较缓慢,如果把平均浓度用入口流率归一化,能看到不同流率的分布模式都类似于高斯分布。
3 结束语
本文通过对不同质量流率的粒径为1 μm的颗粒群在平面湍射流场中的输运及弥散进行了大涡模拟,结果显示:
(1)当流率较小时,颗粒相在漩涡外围聚集较多,整体分布模式基本和气流场的流场结构相类似;流率逐渐增加时,会有少部分颗粒从流动区域逃逸到原先静止的流体区域;流率达到0.1kg/s时,在整个射流区域,都相对均匀的分布着颗粒;
(2)质量流率对颗粒相在y方向上的平均浓度分布,仅能影响到其最大值,对分布模式影响相对较小,在流场发展充分时,归一化后不同流率的颗粒平均浓度呈现类似高斯分布。
[1] 刘小云,罗坤,金军,等.气固两相湍流射流中颗粒的统计特性[J].中国电机工程学报,2005,25(9):108-113.
[2] 郑水华,罗坤,樊建人,等.大涡模拟气固两相三维湍流射流[J].浙江大学学报(工学版),2005,39(4):574-578.
[3] Yu Mingzhou,Lin Jianzhong,Chen Lihua,et al.Large eddy simulation of a planar jet flow with nanoparticle coagulation[J].Acta Mechanica Sinica,2006,22(4):293 -300.
[4] Yu Mingzhou,Lin Jianzhong,Chen Lihua,et al.Nanoparticle coagulation in a planar jet via moment method[J].Applied Mathematics and Mechanics,2007,28(11):1 445 -1 453.
[5] 白建基,郑水华,樊建人,等.雷诺数对气固两相圆湍射流影响的实验研究[J].浙江大学学报(工学版),2006,40(3):433-437.
[6] 王玲玲.大涡模拟理论及其应用综述[J].河海大学学报(自然科学版),2004,32(3):261-265.

