灰色模型在西北电网风电发电量预测中的应用

张小奇，白昕，万筱钟，彭明侨，王鹏，向异

（1.西北电网有限公司，陕西 西安710048；2.重庆大学，重庆 400044）

随着国家《可再生能源法》及一系列节能减排政策、法规的陆续出台，西北地区风电进入快速发展阶段，预计2010年底酒泉千万kW级风电基地将投产风电约500万kW，而“十二五”末，西北地区风电规划总装机将达到2 814万kW，约占全网总装机的12%[1]。风电的随机性和波动性给全网的电量平衡和计划管理带来严峻的挑战，科学地预测风电月度发电量对制定全网月度电量平衡计划、优化全网运行方式意义重大[2]。

风电发电量与风电场所处地区气候环境、地形地貌及风电装机容量等多种因素有关，这些因素中有些是已知的，有些是未知的，具有不确立性和灰色性，因此风电电量与其影响因素是一个典型的灰色系统[3-4]。

本文采用灰色预测理论进行西北电网风电发电量预测，并从强随机性序列建模、背景值改造等方面对传统模型进行了改造，同时给出了预测值的置信区间。实例证明，该方法可以为风电发电量预测提供有效的途径。

1 灰色预测模型

灰色预测模型中最基本的是一次拟合参数模型,即GM(1,1)模型[3-8]，它是通过对原始数据进行累加生成得到规律性较强的序列,再用指数曲线拟合得到预测值,即指数增长型，灰色GM(1,1)模型的预测步骤如下：

1）假定原始数据为n元序列

5）白化微分方程求解

上式即为GM(1,1)模型的预测公式。

2 灰色预测模型的改进

2.1 强随机性序列的平滑处理

由于风电出力及发电量呈现强随机性，如果直接用原始数据建模，预测精度往往会很低。因此我们把时间序列1次指数平滑公式S（t）=αY（t）+（1-α）S（t-1）,α∈[0,1]引入到普通的灰色模型中来，对原始数据重新生成，构成一个新的序列，这样就可以把已有的起伏性的原始序列变为规律性增强的指数序列，可以大大提高精度和灰色预测的适用范围。

对于任意随机序列{X（t）},t∈[0,+∞],令S（t）=αY（t）+（1-α）S（t-1）,α∈[0,1],令随机序列{X（t）}的数学期望（均值）为E[X（t）]=e,e代表数学期望的常数，只要证明新序列{S（t）}的随机性弱于原始序列的随机性就可以用新序列做进一步更精确的预测。根据方差和标准差的定义知，它们描述了随机变量的可取值与均值偏差的疏密程度，也就反映了随机性的强弱，所以只要证明序列{S（）t}的方差小于{X（t）}的方差即可。经过严密的推理证明得知[9-11],新序列方差小于原始序列方差，则新序列的随机性弱于原始序列的随机性。

2.2 背景值的改造

在灰色预测模型中，一般取x(1)（k）、x(1)（k-1）的均值作为背景值Z（k），即Z（k）=（x(1)（k）+x（1）（k-1））/2,其出发点是出于某种平均的考虑，从严格的数学意义上来讲并不成立，当序列变化平稳且间隔小时模型偏差较小，但当序列变化急剧时往往产生较大的误差，如图1所示。从图1可以看出，传统背景值Z（k）=（x(1)（k）+x(1)（k-1））/2正是梯形abcd的面积，它与实际曲线所构成的曲边梯形的面积相差ΔS，序列变化越急剧，ΔS越大，模型误差也就越大。

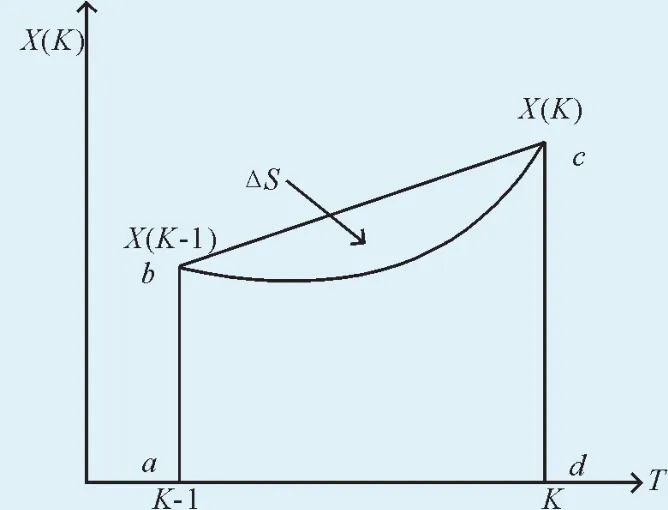
图1 背景值的几何图

基于这种情况，背景值的求解思路为：将区间[K-1,K]进行N等分，将这N个小区间的面积之和近似当作实际曲边梯形的面积。当N较小时，N个小区间面积之和小于实际面积；当较大时，N个小区间面积之和大于实际面积。因此理论上存在一个N值(可以不是整数)，使得N个小区间面积和等于实际面积，如图2所示。

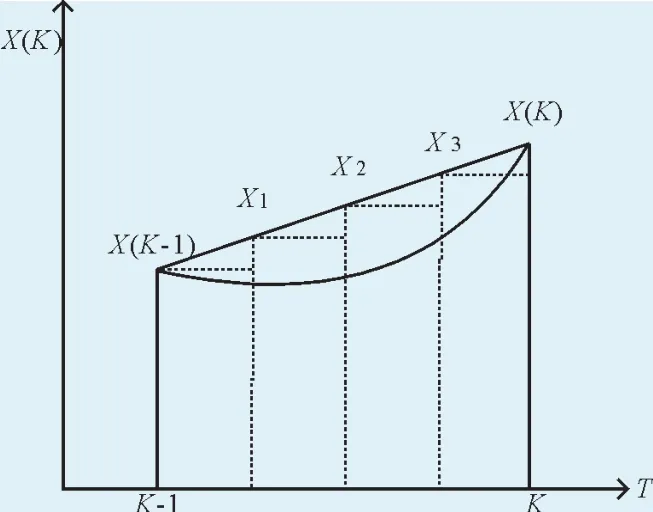
图2 背景值的构思图

容易推导出N个小区间面积之和

β为背景值算子,需要寻找一个β使计算出的背景值建模有最好的精度。本文采用一维搜索的方法，平均相对误差最小的模型所对应的β就是最佳的背景值算子。

3 基于灰色模型的风电发电量预测

3.1 数据维度选择

针对强随机性序列做拟合预测，应尽量利用较新的数据进行预测，数据维度不易过长，否则过于久远的历史数据会干扰预测结果。统计2009年1月至2010年7月西北地区甘肃、宁夏、新疆风电月发电平均负荷率发现，各省风力资源分布具有季节性特点，且每一类大风况基本上维持3～4个月。而灰色预测只要具备4组历史数据就可以建立模型，具有原始数据少、不考虑分布规律、不考虑变化趋势、预算方便、短期预测精度高、易于检验等优点。综上本文采用4维数据建模，同时不断补充新的数据，冲减陈旧历史数据，进行灰色等维滚动预测。

3.2 误差标准

本文采用平均相对百分误差来评价模型的预测能力

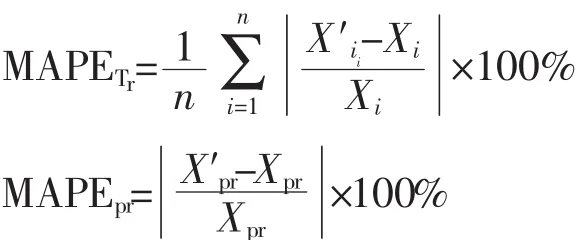
式中,Xii为第i个月的风电实际发电量；X′ii为第i个月的风电拟合发电量；n为建模序列的维度，本文取n=4；MAPETr为预测模型的平均相对拟合误差；Xpr为预测月的实际风电发电量；X′pr为测月的预测风电发电量；MAPEpr为预测模型的平均外推误差。MAPETr可以反映出模型的拟合精度，MAPEpr可以反映出模型的外推精度。

3.3 置信区间

后验差方法虽然可以衡量灰色模型的拟合精度,但不能用来评估模型的预测外推精度,预测值的准确度同原始数列本身的随机性以及与传递误差的系统特性有关[12-15]。因此,对它的估计应以误差在系统内的传播方式与程度来进行。本文用预测值的均方差作为评定预测值准确度的方法，预测值的误差估计为

式中，e（i）为第i个点的拟合绝对误差；e为预测模型的拟合绝对误差向量。

3.3 预测流程

本文利用MATLAB语言开发了基于灰色模型的西北电网风电月度发电量预测程序，具体流程如图3。

图3 预测算法流程图

4 预测实例

我们以西北地区甘肃、宁夏、新疆3省的月风电发电量数据为基础，采用等维滚动预测，检验模型的拟合精度及预测精度。即分别用2010年1~4月、2~5月、3~6月各省的实际风电发电量为历史数据，预测2010年5月、6月、7月的风电发电量，并与预测月份的实际值进行对比分析。2010年1~7月西北各省风电发电量数据见表1，利用灰色模型得到的预测值与实际值的对比如表2所示。

表1 2010年1~4月西北各省风电月发电量108 kW·h

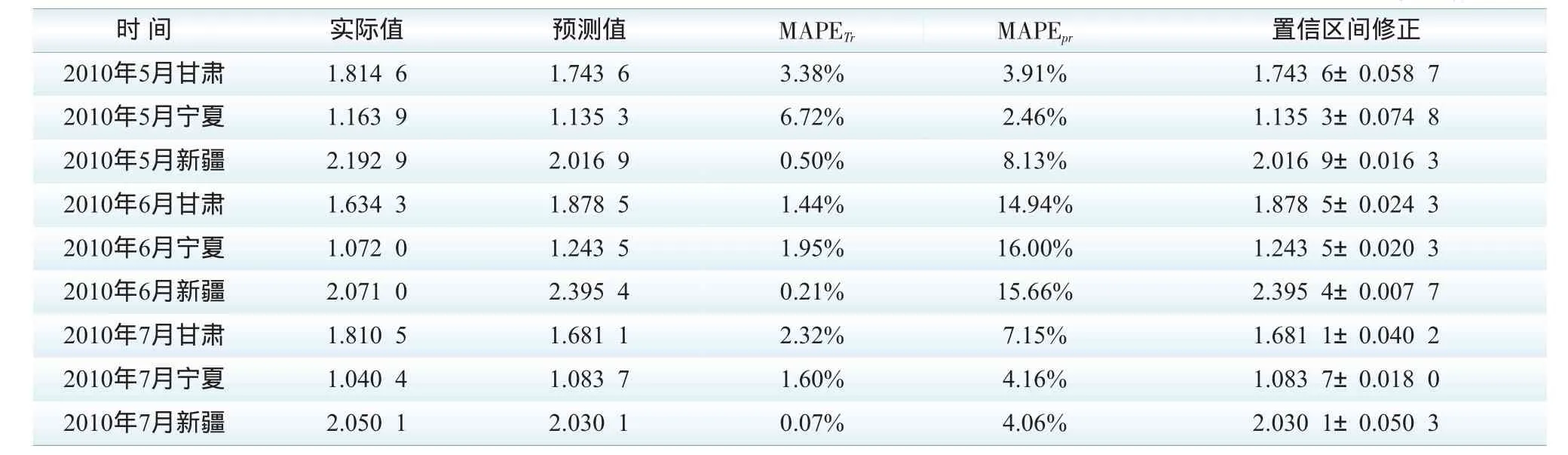
表2 2010年5~7月西北各省风电月发电量预测值对比 108 kW·h

由表2的预测结果可见，本文提出的灰色预测模型拟合误差在7%以内，而外推误差大多在10%以内，基本满足预测要求。从预测范围(置信区间)来看,通过置信区间修正后，预测精度会往往会有所提高。此外，各省在2010年6月份的外推误差达到了15%，主要是因为相应历史数据的离散度较大，导致预测误差增大，但通过更新预测模型的历史数据，模型在7月份的预测取得了较好的效果。可见等维滚动灰色预测模型可以避免预测误差的滚动累加[16-17]，从而提高预测精度。

以2010年7月份的预测为例，给出各省预测结果的对比曲线，及预测结果累加序列的对比曲线，如图4、图5、图6所示。可以看出风电发电量的累加序列与其预测序列拟合度极高，具有很强的指数增长特性，进一步说明灰色模型适用于做短期风电电量预测。

图4 甘肃7月预测曲线对比图

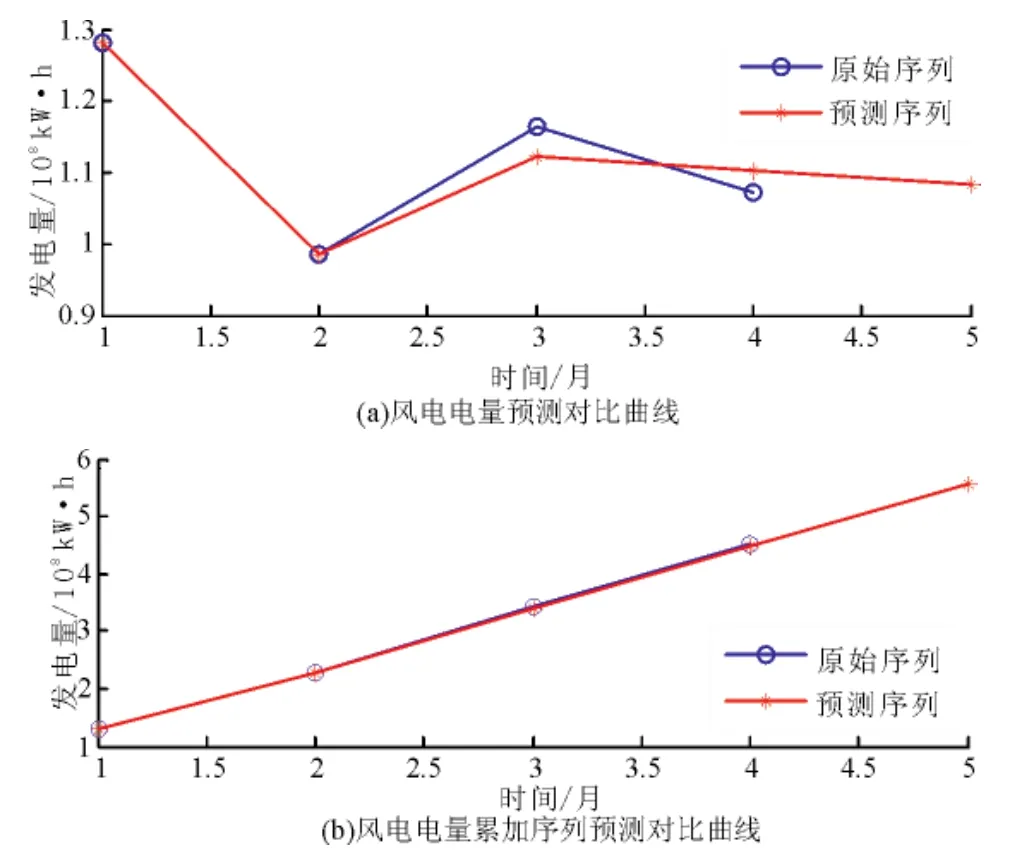
图5 宁夏7月预测曲线对比图

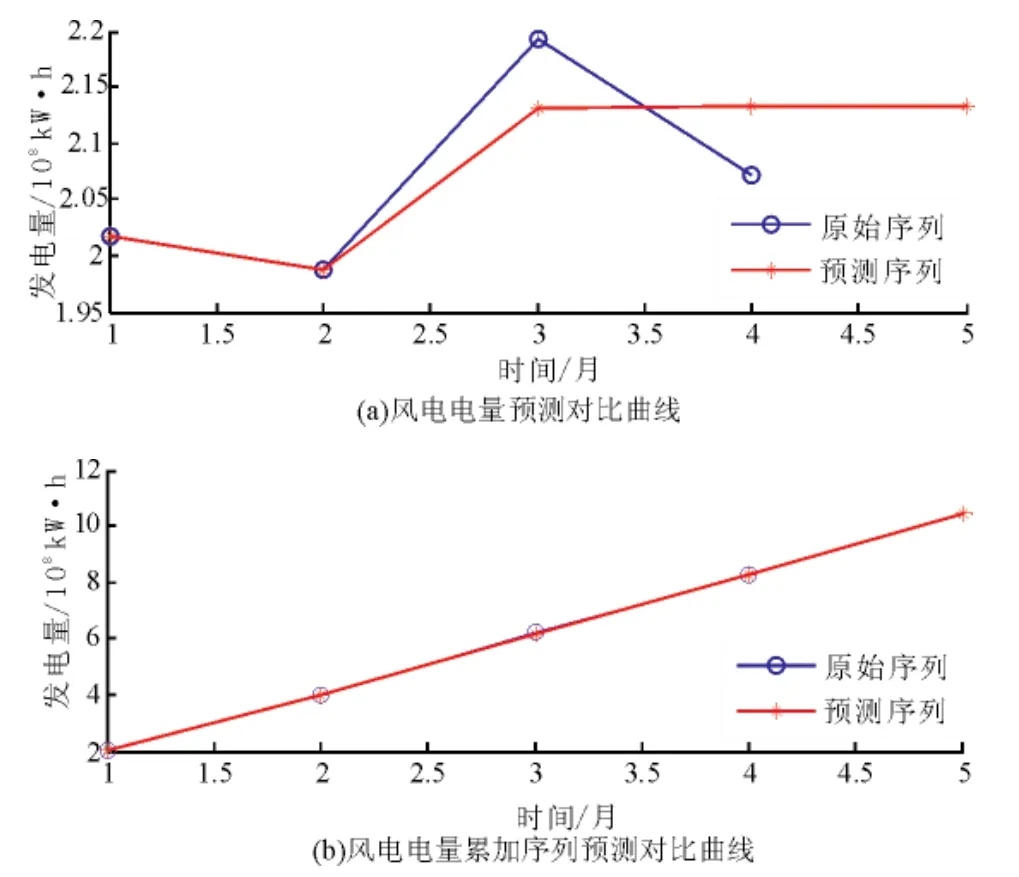
图6 新疆7月预测曲线对比图

5 结论

1）本文采用指数平滑法对随机性较强的风电发电量数据进行了处理，使得原始序列呈现出较强的指数规律，更加符合灰色模型的适用条件。

2）本文提出的模型背景值改造方法及一维搜索寻优方法简单实用，可以提高灰色预测模型的精度。

3）基于误差传播理论，利用拟合误差序列的均方差计算得到外推置信区间对修正模型外推值具有明显的效果。

4）预测模型维度的选取，对预测结果影响较大。结合西北风电运行实际，本文通过实验验证，4个历史数据已能反应系统的运行情况。等维滚动预测可以消除陈旧数据对未来趋势的影响，避免预测误差的积累。

5）当历史数据中出现较强的发散点时，灰色预测精度不太理想，还需要完善和提高。

[1] 喻新强.西北电力系统如何应对大规模风电开发与利用[J].电网与清洁能源,2009,25(8):1-6.

[2] 白建华,辛颂旭,贾德香,等.中国风电开发消纳及输送相关重大问题研究[J].电网与清洁源,2010,26(1):14-17.

[3] 高阳,陈华宇,欧阳群.风电场发电量预测技术研究综述[J].电网与清洁能源,2010,26(4):60-63.

[4] 刘烨,卢小芬,方瑞明,等.风力发电系统中风速预测方法综述[J].电网与清洁能源,2010,26(6):62-66.

[5] 邓聚龙．灰色系统理论教程[M]．华中理工大学出版社,1990．

[6] 邓聚龙.灰色系统基本方法[M].华中理工大学出版社,1986.

[7] 傅立．灰色系统理论及其应用[M]．北京:科学技术文献出版社,1992．

[8] 刘思峰,党耀国,方志耕．灰色系统理论及其应用[M]．北京:科学出版社,2004．

[9] 刘琼,刘琳,刘全．用最优化灰色理论进行电力负荷预测的研究[J]．东北电力技术．1998(03):17-22．

[10]张建华,邱威,刘念,等.正交设计灰色模型在年电力负荷预测中的应用[J].电网与清洁能源,2010,26(2):28-32.

[11]袁保奎,郭基伟,唐国庆．应用灰色理论预测变压器等充油设备内的油中气体浓度 [J]．电力系统及其自动化学报，2001，13(3):40-42．

[12]蔡常丰.数学模型建模分析[M].北京:科学出社,1995.

[13]Vladimir N Vapnik．统计学习理论的本质[M]．张学工，译．北京：清华大学出版社，2000.

[14]张学工．关于统计学理论与支持向量机[J]．自动化学报，2000，26(1):32-42．

[15]王振龙,胡永红．应用时间序列分析[M]．北京；科学出版社,1990．

[16]王鹏,向异,陈妮.基于协同进化算法的西北电网无功优化[J].南方电网技术,2010,4(5):71-74.

[17]高玉洁.风电场接入电网后的电能质量问题分析[J].南方电网技术,2009,3(4):68-72.