基于序贯蒙特卡罗和w ell-being模型的风/柴/储能发电系统可靠性分析
王银莎,栗文义,郭鑫,王瑞刚,刘鑫,赵鹏,巴根
(1.内蒙古工业大学电力学院,内蒙古呼和浩特010080;2.内蒙古包头供电局,内蒙古包头014030;3.内蒙古呼和浩特供电局,内蒙古呼和浩特010000;4.The System Planning Department,Manitoba Hydro,Winnipeg,Canada,R3T0P4)
由于内蒙古地域辽阔,风资源丰富,且边远农村牧区对电力需求的特点,因此风/柴/储能等离网式发电系统在这些地区得到了广泛的应用[1-2]为了给这些地区提供稳定可靠的电能,对该地区的风/柴/储能发电系统进行准确的可靠性评估显得尤为重要。目前对电力系统可靠性评估的方法主要分为确定性和概率性两大类。确定性法的主要缺点是只能预想一些故障重数较少的故障事故后果,不能给出事故发生可能性的确定值[3-4]。概率分析法分为解析法和蒙特卡罗法[5-6]。序贯蒙特卡罗模拟法(Sequential Monte Carlo,SMC)能够容易处理各种实际运行控制策略,具有广泛的适应性等优点,但其计算时间长、要求内存容量大[7-8]。Well-being模型是将确定性准则和概率方法相结合的方法,可以弥补确定性准则和概率法的不足[9]。本文运用序贯蒙特卡罗模拟法和well-being模型对风/柴/储能发电系统进行可靠性评估,并对两种方法进行研究和比较。
1 评估方法
1.1 序贯蒙特卡罗模拟法
序贯蒙特卡罗模拟法是一种以概率统计理论为基础的数值计算方法,也称为状态持续时间抽样法[10-11]。在某一时间尺度内,基于元件状态持续时间概率分布,对电力系统进行仿真模拟。
序贯蒙特卡罗模拟法是通过发电机时间序列和负荷状态时间序列获得系统的发电裕度,如图1所示。其中Ti表示发电系统能够满足负荷需求的时间间隔,ti表示发电系统不能够满足负荷需求的时间间隔,ei表示每种状态下不能满足负荷所需电能的值。

图1 容量状态和负荷时间序列叠加图Fig.1 Superim position of the capacity states and the chronological load pattern
序贯蒙特卡罗模拟法通过统计ti和ei计算发电系统的可靠性指标[9],计算失负荷期望值(Lossof Load Expectation,LOLE)[12]公式为

1.2 Well-being模型
Well-being模型是在概率框架下结合确定性准则对发电系统可靠性进行评估,先通过系统充裕度水平确定性标准判定系统的状态,将系统分为3种状态:1)健康状态;2)边界状态;3)风险状态;然后用概率方法计算发电系统充裕度指标,详细分析和评估孤立发电系统[13-14]。
如图1所示,well-being模型也是通过发电机时间序列和负荷状态时间序列获得系统的发电裕度。Well-being模型通过统计ti和Ti计算发电系统的可靠性指标。计算方法如下:如果储能设备储存的电能(Energy Stored in Battery,ESIB)大于或等于平均负荷(Average Load,AL)或峰值负荷(Peak Load,PL)与投运小时数(Number of Autonomous Hours,NAH)的乘积时,系统处于健康状态,此时Ti是系统所处健康状态的时间间隔,用Ti(H)表示;如果ESIB小于AL或小于PL与NAH的乘积时,系统处于边界状态,此时是系统所处边界状态的时间间隔,用Ti(M)表示。

系统处于健康状态、边界状态和风险状态总小时数分别用n(H),n(M)和n(R)表示。Well-being模型计算可靠性指标公式如下:
健康状态概率:

2 两种可靠性评估方法的比较分析
2.1 样例系统
本文分别采用序贯蒙特卡罗模拟法和wellbeing模型对样例系统进行可靠性评估,系统模型如图2所示,该系统参考IEEE可靠性测试系统(IEEERBTS)[15],参数如表1所示。系统发电机模型以小时为步长,储能模型的充放电状态时间序列和储能容量时间序列由发电系统时间序列和负荷时间序列确定[16-17]。负荷模型采用IEEE-RBTS中的每小时负荷模型[18],系统峰值负荷为60 kW。

图2 风/柴/储能发电系统评估模型Fig.2 W ind/diesel/storage power system evaluation model

表1 样例系统参数Tab.1 Examp le system data
对系统进行可靠性分析和计算系统可靠性指标时,两种方法考虑问题的角度不同。序贯蒙特卡罗模拟法考虑系统是否满足负荷要求,如LOLE;而well-being模型考虑系统运行状态是否能满足充裕度确定性标准和负荷的需求。
2.2 负荷影响
在小型孤立发电系统中,系统的调节能力有限。发电系统可靠性受负荷随时间变化影响较大。通过分析峰值负荷变化对风/柴/储能发电系统可靠性的影响,可以评估系统承受最大峰值负荷的能力,以便在系统运行过程中及时调整运行策略,保证系统的稳定运行。本文采用两种方法分别对风/柴/储能发电系统进行可靠性评估,结果如图3和图4所示。其中峰值负荷在40~100 kW之间变化,步长为5 kW。
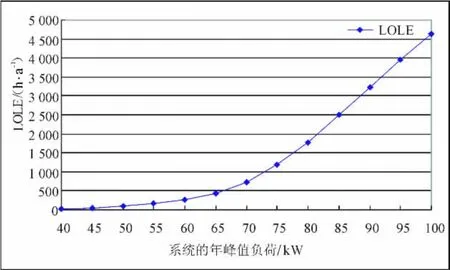
图3 序贯蒙特卡罗方法评估结果随峰值负荷的变化情况Fig.3 SequentialM onte Carlomethod evaluation result w ith the changes of the peak load
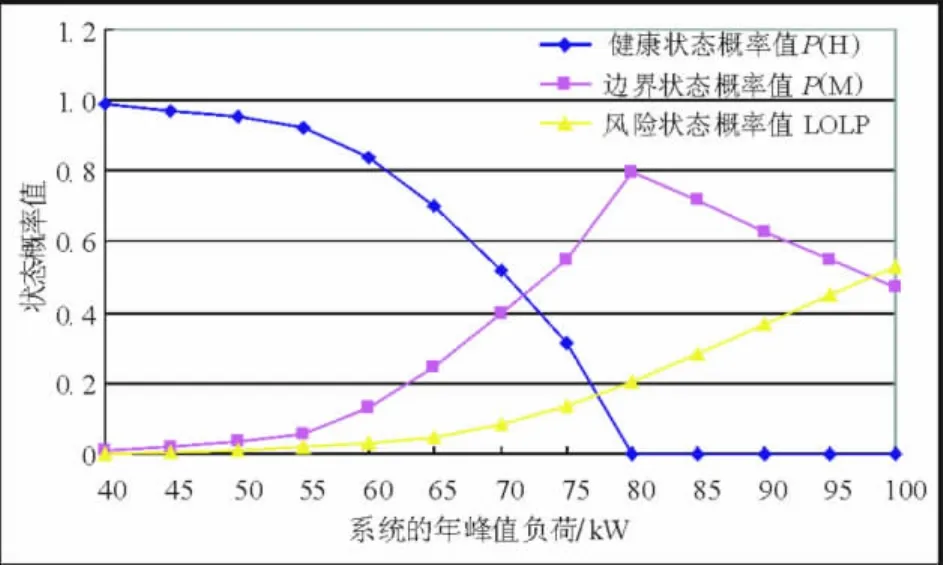
图4 Well-being模型计算结果随峰值负荷的变化情况Fig.4 W ell-beingmodel evaluation resultw ith the changes of the peak load
采用序贯蒙特卡罗方法对系统进行可靠性评估,可以得出峰值负荷对发电系统的影响变化趋势。如图3所示,当系统峰值负荷小于55 kW时,LOLE变化比较平稳,系统的可靠性水平较高;当系统峰值负荷大于55 kW时,LOLE随峰值负荷的增大而迅速增大。但该方法只能计算出发电系统可靠性水平迅速降低的临界点,很难找出系统稳定运行所能承受的最大峰值负荷。
运用well-being模型对系统进行可靠性评估。如图4所示,当系统峰值负荷小于55 kW时,发电系统的各个状态的概率值变化趋于稳定,且系统P(H)值较大,系统在此峰值负荷条件下能够满足系统的充裕度确定性准则,与序贯蒙特卡罗模拟法评估结果相符。随着系统峰值负荷增加,P(H)值减小,P(M)值增加;当系统峰值负荷大于55 kW时P(H)值和P(M)值变化趋势加快。当系统峰值负荷增加到80 kW,此时系统P(H)值为零,P(M)值为系统边界状态概率值的最大值。在峰值负荷55 kW到80 kW之间,系统LOLP值较小,系统不能满足充裕度确定性准则,但仍满足负荷的需求。当系统峰值负荷大于80 kW时,系统的P(M)值减小,LOLP值增大,系统既不能满足充裕度确定性准则也不能满足负荷需求,表明80 kW为维持系统运行所允许的最大峰值负荷。
2.3 储能容量影响
储能设备在风/柴/储能发电系统中发挥着重要的作用,储能容量的多少关系到发电系统的充裕度的大小和供电可靠性的高低。本文分别用两种方法对系统在不同储能容量运行状态下的可靠性进行评估,如图5和图6所示。系统储能容量变化范围为0~700 kW·h,步长为50 kW·h。

图5 序贯蒙特卡罗方法评估结果随储能容量的变化Fig.5 SequentialM onte Carlomethod evaluation result w ith the changes of the battery capacity

图6 Well-being模型计算结果随峰储能容量的变化Fig.6 W ell-beingmodel evaluation resultw ith the changes of the battery capacity
序贯蒙特卡罗模拟法评估结果如图5所示,当储能容量达到450 kW·h后,系统失负荷期望值LOLE变化趋于稳定,系统可靠性高;随着储能容量的继续增加,储能容量对系统的可靠性影响作用减小。当储能容量大于450 kW·h时,系统可靠性较高,但无法得知维持系统满足负荷需求运行的储能容量最小值。
Well-being模型评估结果如图6所示。当储能容量大于225 kW·h后,随着储能容量的增加,系统的P(H)值增加,当储能容量大于450 kW·h时,系统的P(H)值增加趋于平缓,此阶段系统满足充裕度确定性标准,系统可靠性较高,与序贯蒙特卡罗模拟法评估结论一致。计算表明当储能容量为225 kW·h时,系统P(H)值为零,P(M)值为0.964,LOLP值为0.056,系统为边界运行状态。当储能容量在100~225 kW·h,系统的P(M)值较大,系统不能满足充裕度确定性标准,但仍能满足系统负荷的需要。这表明100 kW·h是系统满足负荷需求的最小储能容量。
3 结论
本文介绍了序贯蒙特卡罗模拟法和well-being模型两种可靠性评估方法,并分别对样例系统进行了可靠性评估。通过比较分析两种方法的评估结果,前者可描述可靠性水平随峰值负荷和储能容量的变化趋势;后者不仅可以得出与前者评估结果相符的结论和准确度,又可对系统运行状态进行全面分析,并计算出系统各个运行状态的概率值,同时还能计算出维持系统运行的最大负荷和最小储能容量值。
[1] 陈达,张玮.风能利用和研究综述[J].节能技术,2007,4(25):339-343.CHEN Da,ZHANG Wei.Exploitation and Research on Wind Energy[J].Energy Conservation Technology,2007,4(25):339-343(in Chinese).
[2] 申宽育.中国的风能资源与风力发电[J].西北水电,2010(1):76-81.SHEN Kuan-yu.Wind Energy Resources and Wind Power Generation in China[J].Northwest Hydropower,2010(1):76-81(in Chinese).
[3] 郭永基.电力系统可靠性分析[M].北京:清华大学出版社,2003.GUOYong-ji.PowerSystem ReliabilityAnalysis[M].Beijing:Tsinghua University Press,2003(in Chinese).
[4] 邵伟明.运行方式对供电可靠性的影响 [J].能源工程,2000(6):25-27.SHAOWei-ming.Analysisof the EffectofOperation Scheme on Power Supply Reliabilit[J].Energy Engineering,2000(6):25-27(in Chinese).
[5] 宋晓通.基于蒙特卡罗方法的电力系统可靠性评估[D].山东:山东大学.博士论文.2008.SONGXiao-tong.Study on Reliability Evaluation of Power System based on Monte Carlo Simulation[D].Shandong Shandong University,2008.(in Chinese)
[6] 刘晋,苏虎成,袁 ,等.基于序贯仿真法的复杂配电系统可靠性评估[J].陕西电力,2009(6):17-20.LIU Jin,SUHu-cheng,YUANZhe,etal.Sequential Simulation Based Method for Reliability Evaluation of Complex Distribution System[J].Shaanxi Electric Power,2009(6):17-20(in Chinese).
[7] 孙燕燕.山东500 kV电网发输电系统可靠性评估[D].山东:山东大学,2007 SONG Yan-yan.Shandong 500 kV Power Transmission System Reliability Evaluation [D].Shandong:Shandong University,2007(in Chinese).
[8] 杨飞虎.电网运行可靠性评估分布式算法研究及软件实现[D].合肥:合肥大学,2006.Yang Fei-hu.Research on the Distributed Algorithm of Operational Reliability Evaluation of Power Network and Sftoware Implementation[D].Hefei:Hefei University of Technology,2006(in Chinese).
[9] Bagen,Roy,Billinton.Incorporating Well-Being Considerations in Generating Systems Using Energy Storage[J].IEEE Transactions on Energy Conversion.2005,20(1):225-230.
[10]司媛媛.变速恒频双馈风力发电模拟监测系统[D].合肥:合肥工业大学,2006:12-13.SIYuan-yuan.VSCFDoubly Fed Wind Power Generation Imitation Supervisory System[D].Hefei:HefeiUniversity of Technology,2006:12-13(in Chinese).
[11]张亮,赵娜.基于BP神经网络Monte Carlo法的结构可靠性分析[J].现代电子技术,2010(12):59-61.ZHANG Liang,ZHAO Na.Structure Reliability Analysis Based on BP Neural Network Monte Carlo Method[J].Modern ElectronicsTechnique,2010(12):59-61(in Chinese).
[12]栗文义,张保会,巴根.风/柴/储能系统发电容量充裕度评估[J].中国电机工程学报,2006,26(16):62-67.LIWen-yi,ZHANG Bao-hui,Bagen.Capacity Adequacy Evaluation ofWind-Diesel-Storage System[J].Proceedings of the CSEE,2006,16(26):62-67(in Chinese).
[13]GREGOR Taljana,AndrejF,Gubina.Energy-based System Well-being Analysis for Small Systems with Intermittent Renewable Energy Sources[J].Renewable Energy,2009(34):2651-2661.
[14]张湘艳,卫志农.风力发电对孤立系统电源可靠性的影响[J].江苏电机工程,2006,25(3):58-60.ZHANGXiang-yan,WEIZhi-nong.ImpactofWind Engergy on the Reliability of Small Isolated Power Systems[J].Jiangsu ElectricalEngineering,2006,3(25):58-60(in Chinese).
[15]BAGEN,ROYBillinton.ImpactsOfEnergyStorageOn Power System Reliability Performance[C].2005 IEEECcece/Ccgei.Saskatoon.2005.
[16]ALLAN R N,BILLINTON R,GOEL L,et al.A Reliability Test System for Educational Purposes-basic Distribution System Data and Results[J].IEEE Trans.Power System,1991(6):813-820.
[17]聂继华,杨宜民.风/光互补发电系统的优化设计[J].节能,2008(10):50-52.NIE Ji-hua,YANG Yi-min.Optimization Design of Wind/Photovoltaic Hybrid Power Systems[J].Energy Conservation,2008(10):50-52(in Chinese).
[18]BILLINTON R,BAGEN,C UI Y.Reliability Evaluation of SmallStand-AloneWind Energy Conversion Systems Using a Time Series Simulation Method[J].Proc Inst Elect Eng,Gen,Transm Distrib,2003,150:96-100.

