一种病变眼底图像的配准方法

魏丽芳 潘 林 余 轮

（福州大学计算机图象图形研究所，福州 350002）

引言

眼底图像配准技术在辅助眼科诊断和治疗过程中有着广泛的应用［1-2］。通过配准眼底图像，医生能够更好地诊断和检测各种与眼底相关的疾病，如糖尿病、青光眼、黄斑部变性等，图1给出两幅病变眼底图像示例。

近年来，各种眼底图像配准技术已得到广泛研究，目前眼底图像配准方法主要分为基于灰度的方法和基于特征的方法［3］。基于图像灰度的配准方法直接利用图像的灰度值来确定配准的空间变换，其充分利用图像中所包含的信息；但基于灰度的方法容易陷入一个局部极小值，而且变换模型的搜索空间是巨大的。基于特征的方法是以待配准图像对之间存在的对应特征点（如血管分支和交叉点）为基础，通过测量对应点之间的相似性最值完成。鉴于两种方法的特点，基于特征的眼底图像配准算法得到越来越多的应用。Can等提出层次匹配方法［2］，基于血管分支和交叉点，对于血管分支和交叉点的提取利用了血管追踪和特征抽取的模式。Zana等利用形态学方法提取血管树，将血管树分支和交叉点（特征点）用邻近血管的方向进行标注，实现每对匹配的特征点之间的角度不变性［4］。但这类方法仍然依赖于眼底血管结构的提取。文献［3］将适合曲面配准的迭代最近点iterative closest point，ICP）算法引入眼底图像配准，提出双重引导的迭代最近点算法（dual-bootstrap iterative closest point，DB-ICP）。该算法对于眼底的曲面结构可以获得精确的配准，在较好初值的前提下，算法具有较好的收敛性。但DB-ICP秉承了ICP算法耗时大的缺点，而且对于低质量的眼底图像，也很难配准成功。文献［5］则将尺度不变性特征变换（scale invariable feature transformation，SIFT）引入眼底图像配准，但使用的随机抽样一致性算法（random sample consensus，RANSAC）算法进行初始估计，它在去除误匹配同时也去除了大量正确匹配特征。图1为糖尿病诱发的眼底病变示例。

图1 不同病变的眼底图像。（a）增殖性糖尿病视网膜五期玻璃体病变；（b）非增殖性糖尿病视网膜三期出血灶病变Fig.1 Different pathological retinal images.（a）proliferative diabetic retinopathy Ⅴ vitreous gel pathologic；（b）nonproliferative diabetic retinopathy Ⅲ hemorrhagic foci pathologic

针对病变眼底图像血管结构模糊同时也具有复杂的球体解剖学结构和光学图像系统的特点，提出了一种基于不变特征的眼底图像配准方法。首先提取SIFT特征作为匹配的特征点，提出了双边“或”的best-bin-first（BBF）特征匹配算法对特征点进行初始匹配，通过SIFT特征点的方向特征和空间几何特性去除误匹配，精化匹配特征对，并保留足够的正确匹配对；根据获得的匹配特征通过迭代加权最小二乘法和M-估计进行参数估计，实现病变眼底图像的精确配准。

1 特征提取与匹配

1.1 特征点的提取

图像不变特征（如，角点、SIFT、SURF）和描述符的不断发展为图像精确配准提供了有利的前提［6-9］。在之前的研究中已经证明SIFT算法在眼底图像配准中的有效性［5］。SIFT特征检测算法详见文献［8-9］，是一种基于尺度空间的、对图像缩放、旋转甚至仿射变换保持不变性的图像局部特征描述算子，该算法首先在尺度空间进行特征检测，并确定关键点的位置和关键点所处的尺度，然后使用关键点邻域梯度的主方向作为该点的方向特征，以实现算子对尺度和方向的无关性。其对旋转、尺度缩放、亮度变化保持不变性，对视角变化、仿射变换、噪声也保持一定程度的稳定性，并对每一个关键点产生一个128维的特征描述符以作为匹配依据。

1.2 特征匹配

为了提高特征正确匹配率，同时确保具有足够的匹配对应用于图像的两两配准，提出一种双边“或”的Best-Bin-First（BBF）算法建立两个图像特征点之间的相应性，利用特征点的方向信息和空间几何信息去除误匹配，尽可能地保留正确的匹配。

根据特征点的邻域信息建立高维特征描述符，通过最近邻比值方法，由逼近高维空间的最近邻搜索的BBF算法找到待匹配图像中对应的特征匹配点对［9-10］；BBF算法通过寻找最近邻和次近邻，同时对最近邻与次近邻的比值设定阈值T（文中T取0.5）。

设图像I1和I2的SIFT描述符分别是DES1和DES2，计算相应的距离［10］：

式中，·代表向量的点积。这个集合包含了des与I2中所有描述符之间的距离。dess对应于Dis的最大元素，表示des的最近邻。如果最近邻距离与次近邻距离的比值小于T，则说明构成最近邻的两点是匹配的，否则就不匹配。该算法可有效达到稳定的匹配：在匹配对中，正确的匹配对应的最短距离应该比错误匹配对应的的最短距离短得多，而在高维特征空间中相似的距离内可能还存在着一些其他的错误匹配，利用次近邻匹配作为这部分空间错误匹配密度的估计。

以上匹配过程是单边匹配的，然而在单边匹配时，存在一些遗漏的正确匹配。对于具有曲面结构的眼底图像，正确的匹配对越多且分布越广泛（重叠区域内），获得的图像对之间的变换关系越精确。基于保留更多正确匹配对的考虑，建立双边的匹配，即找出I1到I2之间匹配和I2到I1匹配，建立I1和I2之间的完全匹配，进一步解决了漏匹配问题。双边“或”的BBF算法在获得更多正确匹配的同时，也获得了更多的误匹配。

为进一步去除初步建立的匹配特征对中的误匹配，首先利用SIFT特征旋转不变性，根据匹配特征的方向一致性初步去除误匹配。然后通过建立对应特征对之间的空间几何关系进行一致性检测，有效去除误匹配。匹配点一致性检测运用类似于文献［11］中的原理，代替计算对应线段比作为它的检测数据。通过对应点空间几何关系-空间斜率和距离进行一致性检测，去除误匹配。它基于这样的事实：对于所有对应特征点对，它们的空间斜率和空间距离应该具有一致性。

当所有点对都是物理对应点时，对应的空间斜率和空间距离应是一样的。一致性检测首先对所有线段比值数据进行分级聚类，找出一致性数值。然后通过空间斜率和空间距离数据处理，迭代删除伪匹配对。空间几何关系的一致性检测算法详细描述如下：

步骤1：计算所有对应特征点对的空间斜率p_theta和空间距离p_dis

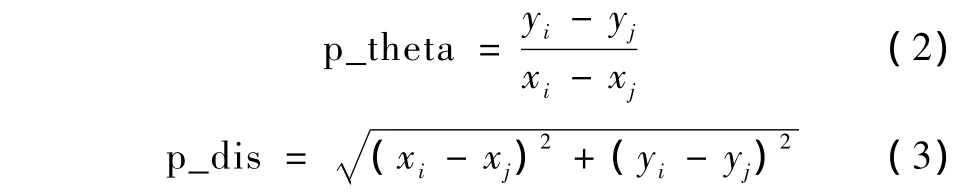
式中，（xi，yi）和（xj，yj）分别为I1和I2中相对应的匹配特征点对。

步骤2：对得到的两组数据分别进行分级聚类，使聚类结果的类别数少且类内距离足够小。聚类结果若有某一类样本个数大于3，且大于其它类的样本个数，则该类样本值称为一致性数值。

步骤3：统计其余样本的非一致性数据个数和一致性数据的方差。

步骤4：将非一致性数据个数值最大的样本集作为候选样本，然后将方差最大的样本集删除。

步骤5：再次统计剩余样本的非一致性数据个数和一致性数据的方差。

步骤6：若非一致性数据的样本集数仍大于3，且至少有一个样本集统计的值大于0，则转到步骤4；否则，输出保留的一致性数据样本集，两种几何关系一致性检测后保留的样本集中的数据对应的点对即为对应的匹配对。

图2为特征匹配结果。

图2 特征匹配。（a）初始匹配；（b）最终匹配Fig.2 Feature matching.（a）initial match；（b）final match

2 变换模型及参数估计

眼底结构通常近似于刚体，而眼底表面是一个空间的曲面，拥有所有曲面的通性，即能以一定数学表达式来表达，并反映其空间形态的本质特征［12］。文献［13-14］中认为眼底是一个二次曲面，而二次曲面包括了椭球面、球面、抛物面及双曲面。眼底的二次曲面模型，即多项式模型是在相机的弱透视模型和对眼底曲面结构的近似，因此以二次曲面的数学模型近似眼底表面是合理的。点p=（x，y）T和q=（x’，y’）T分别是图像I1和I2中的相应匹配点，两幅图像的空间二次曲面模型的变化关系可表示为［2］

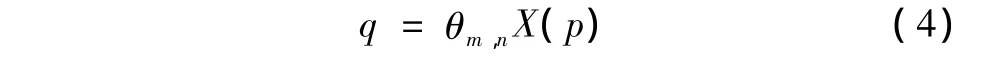
其中θm，n是2×6参数矩阵

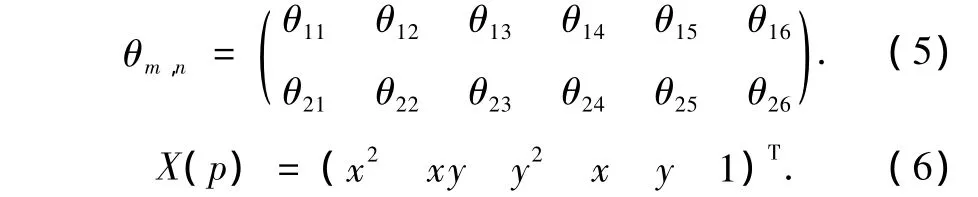
M估计是一种鲁棒的参数估计方法，也可以消除误匹配带来的外点，从而进一步提高估算精度。对θ的M估计算法具体如式（7）和式（8）所示。

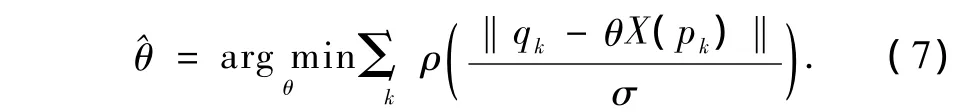
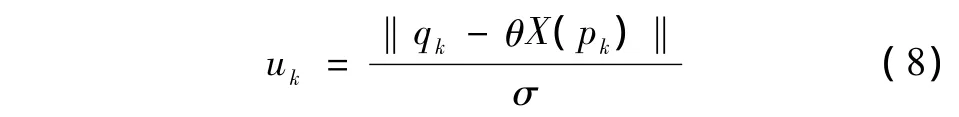
式中，k表示待配准的两图像具有k对匹配的特征点对，ρ是具有鲁棒性损失函数。进行M估计的一个重要技术就是根据实际情况合理选择ρ。常用的三种ρ函数的性能如图3所示［16］，图中横坐标为归一化的误差u，纵坐标为ρ的权重值。根据鲁棒估计理论［15］，σ可通过式（9）计算：

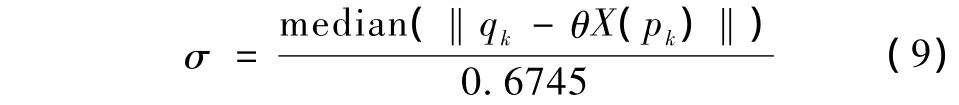
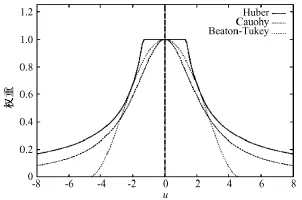
图3 不同损失函数权重值示意Fig.3 Plots of the weight functions for the robust loss functions

由图3可见，Beaton-Tukey函数反应最灵敏，收敛最快，可以有效去除最多的外点，故采用这个函数。

对θ的估计通过迭代加权最小二乘法（iteratively-reweighted least-squares，IRLS）实现。通常情况下，IRLS可以很快实现收敛。

在M估计中，权值函数求解方法为：

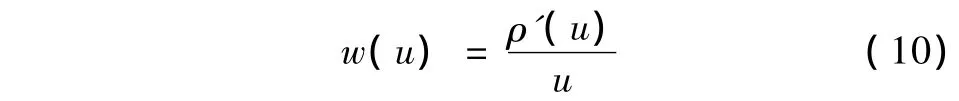
由式（10）可知，Beaton-Tukey函数对应的权值函数为

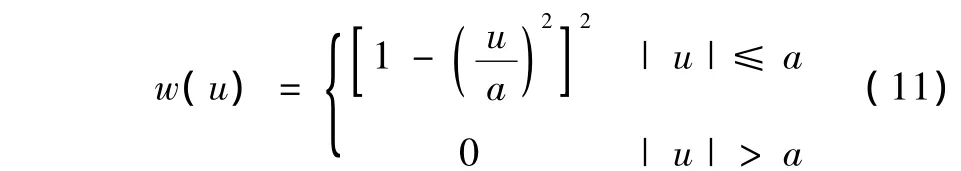
IRLS迭代的初始矩阵取自仿射变换矩阵。

3 算法评估

源图像由福建省附属第一医院眼科提供，图像大小为3 072像素×2 048像素。目标图像共28组，需要说明的是，所讨论方法中一致性检测的实现是基于同组图像尺度变化较小的前提条件。为定量评价本方法的性能，运用正确匹配特征的数量和图像配准精度进行评估。

匹配特征对的数量和分布，是决定参数估计准确性的重要因素。把所采用的双边“或”匹配方法与单边方法及双边“与”方法进行评测。匹配特征的数量评测准则定义如下：令θ表示图像I1和I2之间的映射关系，点p=（x，y）T和q=（x’，y’）T分别是图像I1和I2中的相应匹配点，理想情况下q=θX（p）。实际上，当p和q在空间位置上足够接近时认为匹配关系存在，即‖q-θX（p）‖≤t，则认为p和q是一对正确匹配。实验中选择距离门限t=1.5。

图像配准精度是衡量图像配准算法性能的有效方法。这里采用均方根误差（root of mean square error，RMSE）进行配准精度的测量：

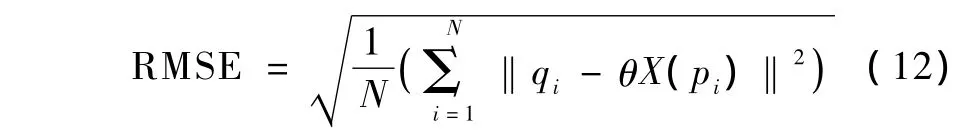
式中，N表示最终得到的正确匹配对的数量。

在检验所提出方法在特征点匹配及配准精度等方面的优势时，对病变眼底图像进行实验。首先通过病变眼底图像的配准结果，说明本方法的有效性；然后利用匹配特征的数量评估指标，对采用双边“或”匹配方法与单边方法的文献［5］和文献［9］及双边“与”方法的文献［10］进行评测；同时计算配准成功图像对的均方根误差评估本方法，并与文献［5］方法所获得的配准精度进行对比，定量描述本方法的优势。

4 结果

对28组实验数据进行实验，其中的27组实验数据配准成功。图4给出了两组不同病变程度眼底图像的配准结果示例，图4（a）的图像受玻璃体病变影响使图像模糊、浑浊，尤其病灶区域血管结构已无法提取，图4（b）的图像受出血灶影响也很难提取完整的血管结构。从两组图像的配准结果中，可以看出配准后的图像保留了有效信息，病变区域及模糊的血管结构均实现了良好的细节对齐，无明显的错误对齐现象，能够满足眼底的医学诊断要求。

在分析正确匹配特征数量的实验中，分析本方法对保留正确匹配对的影响。表1给出了图4中两组示例图像组产生的匹配特征情况，同时比较文献［5］、［9］采用单边方法和文献［10］采用双边“与”方法取得的正确匹配特征的数量。从表1可以看出，本文方法保留了足够的正确匹配对，与双边“与”方法相比能够获得更多的正确匹配对，与单边方法相比也有一定的优势。

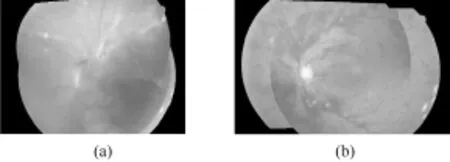
图4 病变眼底图像配准结果。（a）示例1；（b）示例2Fig.4 Pathological retinal image registration results.（a）example 1；（b）example 2

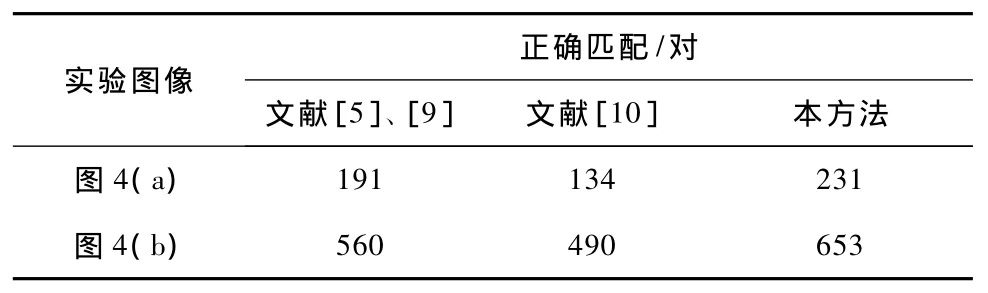
表1 特征匹配方法比较Tab.1 Comparison of feature matching method

利用均方根误差RMSE分析本研究配准成功的27组图像的配准精度。同时与文献［5］采用一般的特征点单边匹配方法结合常用的RANSAC算法（RANdom SAmple Consensus，即随机抽样一致性算法），去除误匹配点的基于不变特征配准方法行进对比实验，其中，经实验统计在28组图像序列中，本方法配准成功27组病变眼底图像，文献［5］配准成功25组。从图5中可看出本方法对每组病变眼底图像的RMSE值均小于1，并浮动于0.5左右，远达到了亚像素级的配准精度。从两种方法的RMSE值的对比可以看出，本方法中每组图像数据的RMSE值均小于文献［5］方法的RMSE值，说明本方法优于文献［5］方法的配准精度。

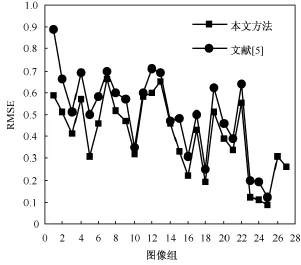
图5 配准精度对比Fig.5 Comparison of registration accuracy

5 讨论和结论

从实验结果可见，采用双边“或”的特征匹配和利用空间几何特性的一致性检测去除误匹配的配准方法的优越性。同时说明在基于特征的配准方法中，准确与丰富的匹配特征在改善和提高配准性能、实现精确配准方面的重要性。因此，采用合适的去除误匹配和保留足够的匹配特征对的方法，对于基于特征的配准方法提高配准精度是有效可行的。本研究的创新点在于合理地运用了特征的双边匹配策略，在基于方向特征去除误匹配的前提下加入了空间几何特性的一致性检测，有助于保留足够的正确匹配特征对，为提高参数估计的精度奠定了基础。

病变眼底图像配准是目前医学眼底图像处理和分析中的一项挑战性课题，其研究工作的开展和研究成果的获得将直接影响到该学科领域的发展和临床眼科诊断水平的提高。在前期研究工作的基础上，提出了一种基于特征的病变眼底图像配准方法。通过28组病变眼底图像进行实验仿真和分析表明，对于不同类型的病变眼底图像该方法都具有较好的配准精度，具有一定的临床参考价值和应用价值。在对匹配特征进行一致性检测时，是基于同组眼底图像尺度变化不大的前提下进行的，如何实现病变眼底图像大尺度变化下的一致性检测及多幅眼底图像配准是下一步研究的方向。

［1］王翠平，李新光，季亚成，等.高血压和糖尿病患者视网膜病变与脑梗死的关系［J］.实用心脑肺血管病杂志，2007，15（2），152-156.

［2］Can A，Stewart C，Roysam B，et al.A feature-based，robust，hierarchical algorithm for registering pairs of images of the curved human retina［J］.IEEE Tran Pattern Ana.Mach Intel，2002，24：347-364.

［3］Stewart C，Tsai CL，Roysam B.The dual-bootstrap iterative closestpoint algorithm with application to retinal image registration［J］.IEEE Trans Med Imag，2003，22（11）：1379-1394.

［4］Zana F，Klein J.A multimodal registration algorithm of eye fundus images using vessels detection and hough transform［J］.IEEE Trans Biomed Eng，1999，18（5）：419-428.

［5］Wei LiFang，Huang LinLin，Pan，Lin，et al.The retinal image mosaic based on invariant feature and hierarchial transformation models［C］//Proceedings Image and Signal Processing，CISP.Tianjin：IEEE，2009：3463-3467.

［6］Harris C，.Stephens MJ.A combined corner and edge detector［C］//Proceedings of the 4th Alvey Vision Conference.Manchester：IEEE，1988：147-152.

［7］Bay H，Tuytelaars T，Gool LV.Surf：Speeded up robust features［C］//Proceedings of the 9th European Conference on Computer Vision.Graz：Springer，2006：404-417.

［8］Lowe D.Object Recognition from local scale-invariant features［C］//Proceedings of the International Conference on Computer Vision.Washington，DC：IEEE Computer Society，1999：1150-1157.

［9］Lowe D.Distinctive Image Features from Scale-Invariant Keypoints［J］.International Journal of Computer Vision，2004，60（2）：91-110.

［10］Chen Jian，Smith R，Tian Jie，et al.A novel registration method for retinal images based on local features［C］//Proceedings of IEEE Eng Med Biol Soc.Vancouver：IEEE，2008：2242-2245.

［11］LI H，Manjunath BS，Mitra SK.A contour-based approach to multisensor image registration［J］.IEEE Trans on Image Processing，1995，4（3）：320-334.

［12］邵婷婷，郑穗联，王波，等.正常个体人眼角膜空间形态数学建模路线研究［J］.眼视光学杂志，2005，7（4）：253-256.

［13］Burek H，Douthwaite WA.Mathematical models of the general corneal Surface［J］.Ophthal Physiol Opt，1993，13（1）：68-72.

［14］Richard L，George S，et al.Descriptors of corneal shape［J］.Op2tom Vis Sci，1998，75（2）：156-158.

［15］Rousseeuw PJ，Leroy AM.Robustregression and outlier detection［M］.New York：John Wiley ＆ Sons，1987：216-247.

［16］Stewart C.Robust parameter estimation in computer vision［J］.Society for Industrial and Applied Mathematics.1999，41（3）：513-537.