基于粘附功的复合推进剂AP/基体界面损伤宏细观仿真①

赵玖玲，强洪夫

(西安市第二炮兵工程学院，西安 710025)

0 引言

复合固体推进剂是一种高填充比的颗粒复合材料，其复杂的力学行为是由其细观结构和在力学载荷下多尺度的物理过程所引起的。已从实验上［1］证实，氧化剂颗粒/基体界面的脱湿是影响固体推进剂力学性能的一个关键因素，从细观角度探索其损伤机理已成为当前研究的一个热点。从细观研究推进剂脱湿机理主要有解析法(细观理论力学)、模拟法(细观计算)及混合法等3种方法。Tan H［2］用Mori-Tanaka方法研究了推进剂的非线性脱粘过程，彭威［3］通过细观力学方法研究了颗粒形状、颗粒间相互作用对总体应力应变关系的影响。研究表明［4］，细观解析方法计算量小，能抓住宏观响应的主要特征，但不能抓住损伤过程中颗粒间的应力集中作用。因此，只能对低体积分数模型进行分析，对于高体积分数模型则失效。而细观有限单元法为复合固体推进剂细观研究提供了很好的数值分析工具，可克服细观理论力学的对体积分数的局限性。彭威［5］通过有限元方法研究了单颗粒材料颗粒分数刚度对分布应力的影响;袁嵩［6］通过有限元方法计算了单颗粒胞元模型在界面粘结完好和存在脱粘2种情况下颗粒与基体的应力分布;李高春［7-8］基于细观有限元和Mori-Tanaka方法分析了界面脱粘，未考虑颗粒粒径效应;曲凯［9］基于粘聚力模型研究了单颗粒胞元在不同界面模型、颗粒粒径和体积分数下的应力-应变曲线，但没对颗粒间相互作用对脱粘影响过程进行深入研究。基于混合法的细观力学，基本思想是细观到宏观的均匀化方法，以从细观胞元推出宏观力学性质，能有效通过各种细观参数对宏观现象的影响进行延伸讨论，有益于从本质上解释脱湿现象。Matouš K［10］用多尺度渐近变分方法和三阶段脱粘模型研究了推进剂胞元模型的脱粘过程，能反映出紧密相关粒子间的复杂作用，其应变范围仅为1%，没有考虑代表体元的大小，且脱粘模型参数的确定无实际的物理基础。

为深入研究复合推进剂界面脱湿机理，本文自主开发了双尺度有限元界面损伤分析平台，并采用点滴法和Washburm毛细管上升法相结合的方法测得了基体与AP颗粒的接触角，然后基于Young's方程计算得界面的粘附功作为界面模型的输入参数，通过小参数渐近扩展数学均匀化方法和蒙特卡洛随机采样平均化方法，得到不同推进剂胞元的宏观力学性能，最后通过定制不同体积分数简化推进剂的拉伸试验，验证了所建立的从实验到仿真的宏细观双尺度方案在研究推进剂脱湿机理方面的可行性和正确性。

1 界面脱湿双尺度有限元模型

1.1 界面单元本构

建立界面脱粘模型是对推进剂材料进行力学分析和损伤评价的出发点。由于界面层很薄，处于纳米到微米量级，因此在力学分析中考虑界面相是不现实的，而将界面理想化为一个面，进而分析出能描述界面受力或变形状况的参数方法，在连续介质力学的范畴内是合理的［11］。本文采用双线性界面本构［12］，将界面模型化为一个具有相应强度等相关特性的无厚度面，基体和颗粒的拉伸强度取决于界面的粘结性能。

对于双线性本构，脱粘牵引力的法向和切向分量Tn和Tt通过式(1)～式(3)与法向和切向张开位移δn和δt关联，曲线如图1所示。

式中 σmax和 τmax分别为拉伸和剪切界面强度;δmax为法向和切向临界张开位移，表征损伤开始的位移;和为切向和法向的完全脱粘位移。

法向和切向通过参数ζ耦合，ζ是衡量脱粘位移程度的无量纲量:

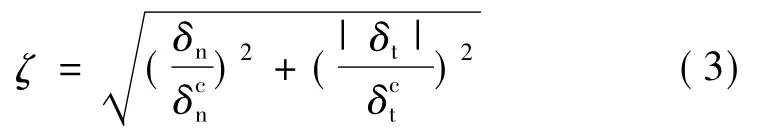
可见，表征界面本构的关键参数有3个:界面初始模量、临界脱粘位移、完全脱粘位移。

图1 双线性界面本构Fig.1 Bilinear interface model

基于以上的界面本构，考虑颗粒边界两侧的不连续性，在有限元计算中，在界面处引入粘聚力单元。关于粘聚力单元嵌入到有限元中的方法见文献［12-13］。图2表征了界面Γ上牵引力p与相对位移δ的关系。δ≤δmax的3个结点0、1、2在受到牵引力p作用时，上下表面发生了微小的位移，但没有发生界面损伤;δmax＜δ＜δc的3个结点，发生了较大位移，但没有完全分离，即界面发生损伤;δ≥δc的2个结点4、5已完全发生分离，此时界面单元不再具有传递牵引力的能力，即界面失效。

图2 界面单元力学性质Fig.2 Interface element mechanics character

1.2 基于宏细观双尺度变分的均匀化方法

与宏观尺度相比，特征胞元的特征粒径是一个非常小的量。当胞元受外载作用时，胞元场变量(如位移和应力)将随宏观位移的改变而产生变化。但由于细观胞元结构的高度非均质性，使得结构的场变量在宏观位置非常小的邻域内也有很大变化。因此，采用了基于双尺度的数学均匀化方法得到从细观到宏观力学性能的过渡［14］。

2 基于粘附功的界面参数确定

由于颗粒和基体界面层的厚度在微米量级，粘聚力模型参数表征是模拟的一个关键和难题。从图1已知，表征界面本构的关键参数有3个:界面初始模量、临界脱粘位移、完全脱粘位移。从拉伸试件断口的扫描电镜照片可看出［1，15］，颗粒和基体界面属于强界面［15-16］，界面初始模量接近颗粒的宏观模量;且在颗粒粒径尺度上颗粒与基体完全脱粘［15］，可认为完全脱粘位移为颗粒尺度，则关键就是临界脱粘位移的确定。该参数可用双线性线段与横坐标所包围的面积(界面粘附功即为将结合在一起的两相分离成独立的两相外界所作的功)来等价描述。

关于颗粒与基体界面间作用，文献［15］用微热量热技术研究得知，AP与MAPO间的相互作用力以范德华力和氢键为主。接触角实验是表征两相材料间表面能大小的有效手段，可得到基体和颗粒界面间的粘附功。本节首先测得基体与AP颗粒的接触角，再基于Young's方程计算得到界面粘附功，从而使粘聚力模型参数得以确定。

由于AP颗粒属于粉体，而胶片属于固体，其测量接触角的仪器、方法和步骤有所不同。

HTPB粘合体系的基体胶片接触角的测量采用点滴法进行。胶片采用 TDI作为固化剂，固化参数为1.02，其中键合剂MAPO含量为0.05%。

对于AP粉末，由于其具有很小的几何尺寸(纳米级)和多孔性，接触角难以观测。目前，常用的红外压片法［17］因在模压过程中最上层颗粒的塑性形变和表面粗糙度的影响，会使得所测接触角有别于颗粒的真实表面。本文采用Washburm毛细管上升法测量粉体的接触角可最大限度还原真实结果。AP颗粒考虑2种粒度 GA-a(130 ～140 μm)和 GA-b(330 ～340 μm)。

表1为所测量的胶片及AP颗粒在2种分析醇下的接触角测量值。

利用Young's方程，可计算得到填料和基体的热力学参数，继而通过调和平均法可计算出基体和2种颗粒间的粘附功。计算结果为GA-a颗粒与胶片间的粘附功为71.12 mJ/m2，GA-b颗粒与胶片间的粘附功为74.02 mJ/m2，此即为图1所示界面参数中双线段与横坐标所围三角形面积。可见，AP颗粒粒径对粘附功影响不大。

由此可通过粘附功计算得到界面的临界脱粘位移，从而使得表征界面本构的3个参数均得到确定。

表1 胶体及颗粒的接触角测试结果Table 1 Contact angle test results (°)

3 仿真及结果验证

3.1 仿真模型生成

为了仿真推进剂界面脱湿的过程，在平衡计算量和精度的基础上［16］，利用蒙特卡洛随机采样的方法建立了随机分布的6种体积分数的计算胞元模型各30个，胞元中135 μm和335 μm直径的2种颗粒个数比均为28∶2。图4为6种模型的示例。

图3 胞元计算模型示例Fig.3 Sample of calculation model

3.2 边界条件的施加和材料参数的选择

假设复合推进剂材料具有理想周期正方排列，所施加边界如图4所示［12］。

边界条件为

3.3 宏观拉伸验证试验

为验证仿真结果，特制定表2所示的3种推进剂简化配方。由于实际推进剂的组分和级配都非常复杂，在实验方案上，需在不改变真实机理的前提下，对实际配方作适当简化，以分离出无关因素。简化原则为忽略铝粉效应;忽略增塑剂等微量组分;双粒径组批。其中，GA-a和GA-b 2种氧化剂颗粒的级配比例均为7∶3，粘合剂体系与接触角实验中胶片材料完全相同，且同时浇注成型，以减少材料批次因素的影响。

图4 边界条件的施加Fig.4 Boundary condition

表2 简化配方设计Table 2 Design of prescription

通过加工相应标准试件，按照航天工业部标准QJ 924—85“复合固体推进剂单向拉伸实验方法”，在新三思万能电子拉伸机上进行了单轴拉伸实验。为了更有针对性地研究界面脱湿机理，实验采用准静态拉伸(拉伸速率为0.1 mm/min)方法，以排除基体的黏性效应。

图5(a)为3种推进剂配方的应力-应变曲线，可见随体积分数的增加，推进剂力学性能明显增加。图5(b)为基体胶片的应力-应变曲线，可见基体应变在30%以下时表现为线弹性。由图5(b)可得基体的模量参数如表3所示。表3中同时列出了其他材料参数［10］。

3.4 仿真验证及分析

分别通过对6种胞元模型的30个模型进行计算分析，计算结果显示服从均匀分布，与平均值的相对误差在10%以内。表4给出了仿真结果的平均值和实验结果的对比及误差。

图6为3种简化配方推进剂的仿真和实验结果比较。由图6可见，仿真结果与实验结果吻合较好。表5对3 种体积分数 0.47、0.55、0.59 下的初始模量和应变8%时的模量对比，由表5可看出，应变8%时的模量与初始模量相比均有明显下降，且体积分数越大，模量下降越快。

图5 应力-应变曲线Fig.5 Stress and strain relation

表3 仿真材料参数Table 3 Parameter of material

表4 计算结果比较Table 4 Results comparison

图6 模量随初始体积分数的变化Fig.6 Module change with volume fraction

双尺度仿真不仅可得出材料的宏观性能，而且可得到在胞元内部的应力-应变分布情况。图7给出了体积分数为55%胞元模型在不同应变下的应力云图。比较图7(a)和7(b)可见，随应变增加，颗粒/基体界面受到损伤，产生脱粘，界面应力随之降低，导致胞元总体应力降低，从而使推进剂总体模量降低。比较图7(c)和7(b)可见，在较大体积分数下，颗粒间应力集中作用更强，颗粒和基体更易脱湿，从而导致相比低的体积分数，高体积分数下推进剂的模量下降更快。这与表5结论相同。

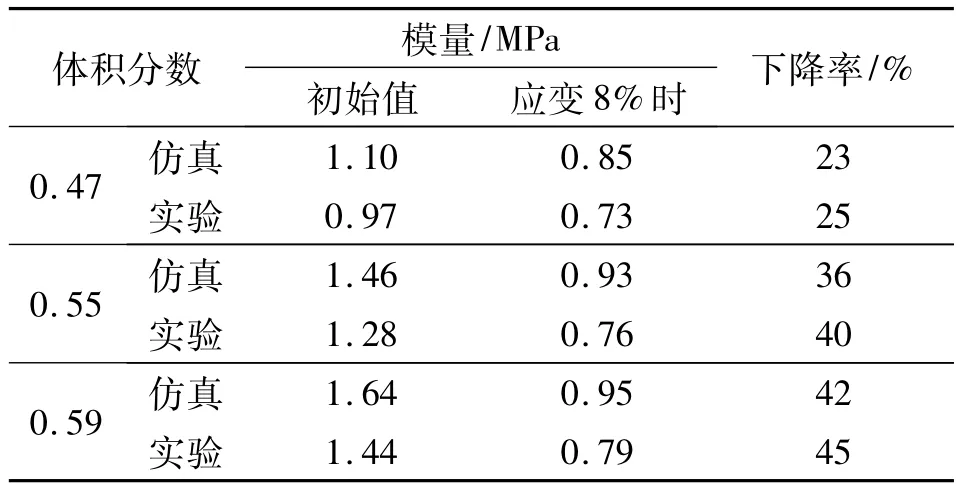
表5 模量下降比例Table 5 Reduction rate of module

图7 应力云图Fig.7 Stress nephogram

4 结论

(1)建立了一套可用于评估复合推进剂细观脱湿损伤的实验与仿真相结合的宏细观双尺度方案，并通过定制简化配方的3种体积分数推进剂的拉伸实验，证明了方案的可行性和正确性，为进一步研究推进剂脱湿机理奠定了基础。

(2)采用点滴法和Washburm毛细管上升法，测得基体与AP颗粒的接触角，再基于Young's方程计算得到的颗粒/基体界面的粘附功可定量表征界面粘结性能，从而使粘聚力界面模型的输入参数有一定的物理基础。

(3)复合推进剂宏细观双尺度仿真方法不仅可得到其宏观应力应变曲线，而且可得到不同应变下的细观应力应变分布情况，为进行推进剂损伤机理的研究提供了一条有效途径。

(4)随应变增加，颗粒/基体界面受到损伤，产生脱粘，界面应力随之降低，导致胞元总体应力降低，从而使推进剂总体模量降低。在体积分数较大时，颗粒间应力集中作用增强，颗粒和基体更易脱湿，从而导致相比低的体积分数，推进剂模量下降更快。

［1］曾甲牙.丁羟推进剂拉伸断裂行为的扫描电镜研究［J］.固体火箭技术，1999，22(4):69-72.

［2］Tan H，Huang Y，Liu C.The mori-tanaka method for composite materials with nonlinear interface debonding［J］.International Journal of Plasticity，2005，21:1890-1918.

［3］彭威，等.复合固体推进剂脱湿模型研究［J］.固体火箭技术，2000，23(2):48-51.

［4］Inglis H M，Geubelle P H，M atous K，et al.Cohesive modeling of dewetting in particulate compo sites:micromechanics vs.multiscale finite element analysis［J］.Mchanics of Materials，2007，39:580-595.

［5］彭威，等.复合固体推进剂应力分布的数值模拟及损伤萌生分析［J］.固体火箭技术，2002，25(1):12-15.

［6］袁嵩，等.复合推进剂的细观失效机理分析［J］.固体火箭技术，2006，29(1):48-51.

［7］李高春，等.基于细观力学的复合固体推进剂模量预估方法［J］.推进技术，2007，28(4):441-444.

［8］李高春，等.固体推进剂界面脱湿有限元分析［C］//2007固体火箭推进24届年会论文集，2007:147-150.

［9］曲凯，等.复合固体推进剂非线性界面脱粘的力学性能研究［C］//2009固体火箭推进26届年会论文集，2009:102-107.

［10］Matouš K，Geubelle P H.Multiscale modeling of particle debonding in reinforced elastomers subjected to finite deformations［J］.Int.J.Numer.Methods Engrg.，2006，65:190-223.

［11］许金泉.界面力学［M］.北京:科学出版社，2006.

［12］周储伟，杨卫.粘聚力界面单元与复合材料的界面损伤分析［J］.力学学报，1999，31(3):372-377.

［13］王瑁成.有限单元法［M］.北京:清华大学出版社，2003.

［14］Cui Jun-zhi，Cao Li-qun.Finite element method based on two-scale asymptotic analysis［J］.Chinese J.Num.Math.A.ppl.，Allerton Press，Inc.，1998，20(2):60-74.

［15］陶伯文.NEPE推进剂填料/基体界面作用表征方法研究［D］.航天科技集团四院42所硕士论文，2009.

［16］Banerjee B.Micromechanics simulations of glass-estane mock polymer bonded explosives［J］.Modeling and Simlulation in Materials Science and Engineering，2003，11:457-475.

［17］余钢，等.用接触角法估算复合材料的表(界)面特性［J］.粘接，2000，21(5):28-31.