某固体火箭发动机推力向量控制系统接头接触性能分析①

刘文芝，戴美魁，韦广梅，赵永忠

(1.内蒙古工业大学机械学院，呼和浩特 010051;2.中国航天科工集团公司六院四十一所，呼和浩特 010051)

0 引言

以某固体火箭发动机全轴摆动推力向量控制(thrust vector control——TVC)系统的摆动接头为研究对象，摆动接头由阴球、阳球、滚动体等组成，工作中既是活动体与固定体间的联接件，又是载荷支承件［1］。在工作载荷作用下，一方面滚动体与阳球接触位置处，阳球材料已产生塑性变形;另一方面，系统不允许太大的变形，当变形超过许可范围，则造成摆动力矩增大，增加推力向量控制的难度。因此，摆动接头设计必须在满足结构质量及接头结构尺寸要求的前提下，保证接头能承受预定的工作载荷而不产生过量的弹塑性变形、具有一定的接触强度。阳球材料一般采用高强度、高韧度合金钢，具有良好的机械加工性能和热处理工艺。摆动接头零件成形后，需进行表面强化处理，形成一定厚度的强化层，强化层使阳球表面具有高接触强度、高承载能力和高耐磨性。

本文采用更符合工程实际的弹塑性摩擦接触有限元法，与单珠承载试验对比分析，为降低系统摆动力矩，同时考虑大尺寸球面(大于等于φ300 mm)的表面强化和加工工艺，计算分析阳球试件经表面强化处理后，在不同强化层厚度下，滚动体与阳球间的接触应力、变形及破坏机理;不同强化层厚度对接头接触性能的影响;确定满足小变形条件的弹塑性摩擦接触应力限额。即使在简单载荷作用下，对于考虑材料强化层和摩擦效应，并与弹塑性耦合的接触问题的简单模型，其解析建模及求解也非常复杂困难，一些数学问题亟待进一步解决［2－3］。用数值法求解虽有一定困难，但它具有相对完善的理论，能广泛适应求解复杂的力学问题，随着计算机的飞速发展，在工程技术领域中，其实用性更强、更为高效。由于无法通过全尺寸TVC系统的接头进行试验验证，本文采用数值计算和简单实验验证相结合的相对简化模型进行研究。

1 弹塑性摩擦接触有限元模型

试验中没有观测到滚动体的残余变形，因此计算模型为弹性滚动体与弹塑性阳球试件的摩擦接触模型，摩擦采用库仑摩擦。

1.1 弹塑性摩擦接触有限元模型

考虑实际问题的特点，选用计算精度高的接触问题Lagrange乘子法。根据广义变分原理，在计算域中，把接触约束条件与Lagrange乘子相乘，与系统原势能(结构材料的弹塑性势能)一起构成一个修正泛函，把接触问题转换成求修正泛函的驻值问题，即无约束泛函的极值问题。离散接触界面，滚动体与阳球试件间建立面-面接触模型。阳球试件表面为接触面，滚动体表面为目标面。把接触力转换成等效节点接触力向量，写入方程左端，并整合为系数矩阵，引入接触定解条件，得到弹塑性摩擦接触问题的有限元控制方程［4－5］。

t+Δt时刻弹塑性摩擦接触有限元控制方程为

设Z、X分别表示接触体在接触界面的法线方向和切线方向。

滑动状态:Kca≠(有摩擦滑动)，Kcλ=(无摩擦滑动)

式中t+ΔtKcp为t+Δt时刻系统弹塑性总刚矩;Δα为系统的位移增量向量;t+ΔtQi为t+Δt时刻的外载荷向量;t+ΔtQ1为 t+Δt时刻的内力向量;tg－为 t时刻接触点对间距;t+Δtλ为 t+Δt时刻拉格朗日乘子(力学意义是接触力)。

如果接触状态变化，可能发生不连续，为避免收敛太慢，在每一载荷增量步内用F.N.R迭代求解，其递推迭代公式为

接触计算判定条件:

粘合状态:t+ΔtRZ＞0，不满足转入分离;

t+ΔtRX－ƒ|t+ΔtRZ＜0，不满足转为滑动。

滑动状态:t+ΔtRZ＞0，不满足转为分离;

对于弹塑性摩擦接触问题，由于2个非线性混合在一起，在1个增量步中，每给定1种接触状态，就要解1个弹塑性边值。弹塑性迭代收敛后，检查接触状态，若接触状态与求解前一致，则该增量步的解已获得。不一致，则必须恢复到增量步开始状态，否则就把非真实接触条件下的变形历史引入后续计算，造成误差甚至错误的结果。然后，用新的接触状态重新求解该增量步，直到弹塑性迭代收敛后，接触状态与求解前假定的一致，得到该增量步弹塑性摩擦接触问题的解。即弹塑性迭代置于内循环，接触迭代置于外循环。

1.2 材料性能及载荷路径

滚动体弹性模量E=2.54×105MPa，泊松比μ=0.3，滚动体半径 r=5 mm。

强化层弹性模量E=2.54×105MPa，泊松比μ=0.3。本构关系为弹性区域σ=Eεe;塑性区域σ=σs+Hεp，其中 εe、εp分别为弹性、塑性应变;屈服极限σs=2 000 MPa，强化系数 H=1 ×104MPa。

材料表面精磨0.1 mm后，滚动体与阳球试件接触表面间的摩擦因数为ƒ=0.003。

阳球试件基体材料的弹性模量E=2.1×105MPa，泊松比μ=0.3，屈服极限σs=1 100 MPa。本构关系为弹性区域σ=Eεe;塑性区域由试验测得，见图1。

有限元计算分析中的加载、卸载路径与单珠承载试验中的加载、卸载路径一致。

图1 阳球基体材料的应力-应变曲线Fig.1 Stress-strain curve of the convex sphere materials

2 有限元计算结果与分析

考虑大尺寸球面(大于等于φ300 mm)的强化和加工工艺，在500 kg载荷作用下，以强化层厚度为1 mm以下(0.5、0.9 mm)和 1 mm 以上(1、1.22、1.4 mm)的阳球试件为算例。

根据单珠承载试验中载荷特性和接触体的几何特性，建立弹塑性摩擦接触二维轴对称有限元计算模型(图2)。

图2 有限元计算模型Fig.2 Finite element computation model

2.1 强化层厚度为1 mm以下阳球试件的接触性能

2.1.1 接触表面应力及变形

图3为阳球试件强化层厚度分别为0.5 mm和0.9 mm时强化层表面接触应力σ及接触半径a分布。

由图3可知:

(1)对不同强化层厚度，阳球试件表面的接触应力、变形分布不同。层厚越薄，受基体较软材料影响越大，接触应力越小，接触变形越大。

(2)层厚0.5 mm和0.9 mm的最大接触应力和接触半径分别为 4 371.1 MPa、0.66 mm 和5 026.2 MPa、0.62 mm。与0.5 mm 强化层厚度相比，0.9 mm 的接触应力增大14.987 1%，变形减小6.060 6%，从这点考虑，似乎强化层越薄越好。但由于TVC系统摆动速度慢，摆动频率低，且实际中接触变形对系统摆动力矩影响大。因此，尚需综合考虑在满足接触应力的前提下，其弹塑性压深的问题。

图3 接触应力及接触半径分布Fig.3 Curves of contact stress and contact radius

图4为阳球试件强化层厚度分别为0.5 mm和0.9 mm时接触表面的弹塑性压深b、卸载后的残余压深b0分布。

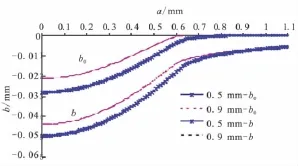
图4 弹塑性压深及残余压深分布Fig.4 Curves of elasto-plastic indentation deepness and residual indentation deepness

由图4可知:

(1)对不同强化层厚度，在接触区域内产生不同大小的弹塑性接触变形，卸载后存在不同程度的残余压深;接触区以外部分区域内，由于变形的连续性，试件表面出现弹性压缩，卸载后恢复。由于弹性恢复，残余接触半径a0小于弹塑性接触半径a。

(2)强化层越薄，受基体较软材料的影响越大。强化层厚为0.5、0.9 mm的试件表面，最大弹塑性压深和最大残余压深分别为 0.049 6、0.028 1 mm 和0.043 9、0.021 2 mm;与层厚0.5 mm 相比，层厚为0.9 mm时，弹塑性压深降低11.491 9%，强化层厚度的增加，明显降低了弹塑性接触压深，有利于降低系统摆动力矩。

(3)为满足系统摆动力矩要求，规定残余压深为0.03 mm［1］。实际应用中，其安全系数为 1.2，则许用残余压深为0.025 mm。层厚0.5 mm试件的残余压深已超过许用残余压深。

2.1.2 层下应力

图5为强化层厚度分别为0.5 mm和0.9 mm时，沿滚动体与阳球接触中心对称轴Z，阳球试件的主剪应力τ和等效Mises应力σV分布。

由图5可知:

(1)不同强化层厚度，阳球试件接触表面下方的主剪应力和等效Mises应力在强化层内分布不同;层厚0.9 mm的试件，在中心对称轴z=0.26 mm的近表层区域内，最大主剪应力和等效Mises应力迅速增长，在z=0.26 mm处达到最大;层厚0.5 mm的试件，主剪应力和等效Mises应力在近表层内持续增长，在z=0.48 mm处达到最大;在z=2.5 mm以后，2种层厚的应力平缓下降，逐渐趋于一致。

(2)在强化层和基体材料的交界面处，不同层厚的应力均有较大突变;层厚越薄，突变程度越大，越容易引起2种材料的层间剥离［6］;基体材料在交界面局部区域内的等效Mises应力均已超过材料的屈服极限，理论上在交界面处已产生初始裂纹［6］。

图5 主剪应力及等效Mises应力分布Fig.5 Curves of main shear stress and equivalent Mises stress

为了满足试件接触变形、减小应力突变、避免层下基体材料塑性变形，阳球试件表面强化层厚度不得小于1 mm。

2.2 强化层厚度为1 mm以上阳球试件的接触性能

2.2.1 接触表面应力及变形

图6～图7为阳球试件强化层厚度分别为1、1.22、1.4 mm时，强化层表面的接触应力σ及接触半径a分布、弹塑性压深b及残余压深b0分布。

由图6、图7可知:

(1)强化层厚度为 1、1.22、1.4 mm，最大接触应力分别为 5 180.7、5 202.9、5 206.0 MPa，最大相差0.488 4%;接触半径均为0.6 mm;最大弹塑性压深分别为 0.037 3、0.036 8、0.036 6 mm，最大相差1.876 7%;残余半径分别为0.58、0.57、0.57 mm，最大相差 1.724 1%;而残余压深分别为 0.016 8、0.016 4、0.016 3 mm时，最大相差2.976 2%。残余压深均满足许用残余压深要求，充分发挥了强化层的作用。

(2)当强化层厚度大于等于1.22 mm时，其接触应力及接触半径分布基本相同，所以其应力和变形基本不受基体较软材料的影响;层厚为1 mm的试件，其接触压深及卸载后的残余压深较其它层厚的试件相对较大，一定程度上仍受基体材料的影响。

(3)与强化层厚度小于1 mm的接触应力和变形相比，最大接触应力增大3.073 9% ～19.100 5%，而最大弹塑性压深减小15.034 1% ～26.209 7%。

因此，强化层厚度的增加，使接触应力较小增加的同时，显著降低了弹塑性接触变形，这对降低TVC系统的摆动力矩有很大意义。

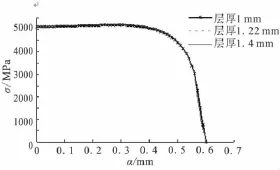
图6 接触应力及接触半径分布Fig.6 Curves of contact stress and contact radius

图7 弹塑性压深及残余压深分布Fig.7 Curves of elasto-plastic indentation deepnessand residual indentation deepness

2.2.2 层下应力

图8 为强化层厚度分别为 1、1.22、1.4 mm 时，沿滚动体与阳球接触中心对称轴z，阳球试件的主剪应力τ和等效Mises应力σV分布。

由图8可知:

(1)不同强化层厚度的主剪应力和等效Mises应力极值均在z=0.28 mm处。强化层厚度为1.22 mm和1.4 mm的层间应力突变较1 mm明显减小，可有效防止层间剥离;不同强化层厚度的阳球试件，基体材料的等效Mises应力小于其屈服极限，层间不易产生初始裂纹。

(2)与强化层厚度小于1 mm的试件相比，当强化层厚度大于等于1 mm时，其层间交界面处的应力突变减弱，减小了材料层间剥离的机率。

(3)层厚越厚，会增加表面脆性压裂的机率［6］，但试验证实，在研究层厚范围内并未产生表面裂纹。

因此，从接触性能及破坏机理考虑，阳球试件强化层厚度必须大于等于1 mm。考虑大尺寸球面加工及强化工艺问题，试件强化层的厚度在1～1.4 mm较合适。

图8 主剪应力和等效Mises应力分布Fig.8 Curves of main shear stress and equivalent Mises stress

3 试验与计算结果的对比分析

直接测量接头内部的接触性能非常困难。采用残余压痕反求弹塑性接触变形和接触应力限额的间接分析计算和试验方法，是解决这一问题较为有效的途径。

3.1 单珠承载试验

在保证强化层厚度要求前提下，阳球试件经强化处理，表面精磨0.1 mm后，用扫描电镜测得其强化层厚度为1.22 mm。材料性能检测结果见1.2节。

滚动体与阳球试件接触，在载荷作用下，阳球试件表面产生弹塑性变形，卸载后有不同程度的压痕。每级加载的压痕不重复。在工具显微镜下，测量并记录压痕宽2a0(表1)，对每级加载条件下的压痕宽取平均值(表1)。

3.2 试验与计算结果的对比分析

在不同载荷作用下，压痕宽的试验测量结果与弹塑性摩擦接触有限元计算结果见表1。

在每级载荷作用下，相对于试验测量平均压痕宽，残余压宽的数值计算结果平均误差为6.153 6%。

3.3 接触性能高载荷验证

图9～图10分别为在1 000 kg载荷作用下，沿滚动体与阳球接触中心对称轴z，阳球试件主剪应力τ和等效Mises应力σv分布等值线有限元计算结果。

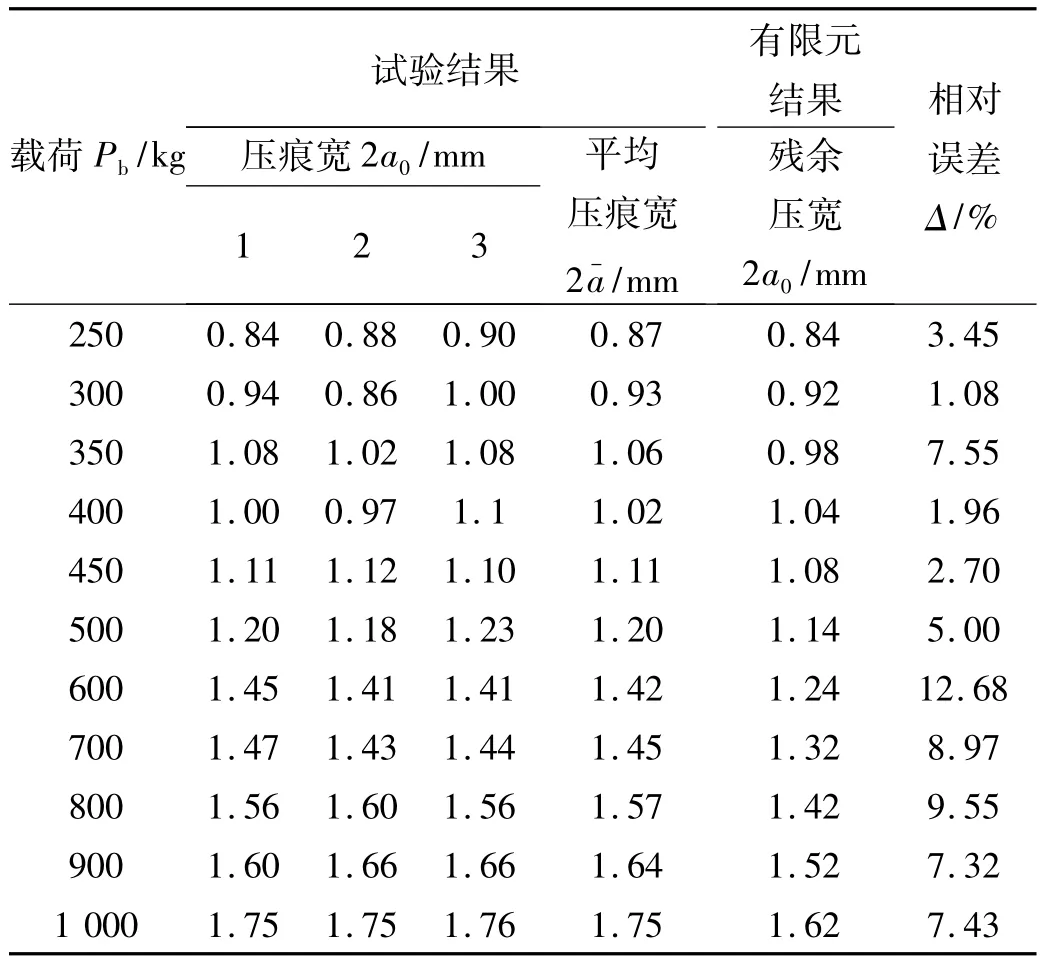
表1 试验结果与弹塑性摩擦接触有限元计算结果Table 1 Test results and computation results of elasto-plastic friction contact finite element method

图9 主剪应力和等效Mises应力分布Fig.9 Curves of main shear stress and equivalent Mises stress

图10 等效Mises应力分布等值线Fig.10 Contour line of equivalent Mises

由图9、图10可知:

(1)载荷达到1 000 kg，层下最大主剪应力和等效Mises应力的位置在沿中心对称轴距接触中心z=0.36 mm处，强化层在 z=0.02 ～1.2 mm 区域内，平行接触表面的部分区域屈服;基体材料未产生塑性变形，层间不易产生裂纹。

(2)在1 000 kg载荷作用下，塑性区域包含在接触区域内，所以在所研究载荷范围内，塑性区全部包含在接触区域内。

在电镜下观察压痕(放大100倍)，并切片检测，试件在250～1 000 kg载荷作用下，均未发现表面裂纹和层间剥离、层间裂纹。

因此，弹塑性摩擦接触有限元算法及其结果合理，通过弹塑性摩擦接触有限元计算分析所提出的强化层厚度要求可靠。

4 接触应力限额

试验和有限元计算结果表明，在载荷作用下，滚动体与阳球试件接触处，阳球试件材料已产生弹塑性变形。表2为在不同载荷作用下，阳球试件表面弹塑性摩擦接触应力、接触变形的有限元计算结果。

表2 弹塑性摩擦接触有限元计算结果Table 2 Results of elasto-plastic friction contact finite element method

由表2可知，滚动体与阳球试件接触，若试件表面残余压深为0.025 mm时，对应的接触应力为接触应力限额。再由表2可知，弹塑性摩擦接触应力限额为5 384.9 MPa，此时试件表面的弹塑性压深为0.049 448 mm，残余压深为 0.024 901 mm。

5 结论

(1)阳球试件的强化层厚度大于等于1 mm，在相同材料性能、相同载荷作用下，层厚越厚，接触应力和变形规律越趋于相同，且满足许用残余压深的要求。与1 mm以内不同层厚的试件相比，接触应力有较小增加，而弹塑性变形显著下降，有利于降低系统摆动力矩。

(2)与强化层厚度小于1 mm的试件相比，当强化层厚度大于1 mm时，强化层与基体材料间交界面处的应力突变减弱，减小了材料层间剥离的机率;基体材料的等效Mises应力小于其材料屈服极限，层间不易产生初始裂纹。

(3)从接触性能及破坏机理考虑，同时为降低系统摆动力矩，满足大尺寸球面的表面强化和加工工艺，阳球试件的表面强化层厚度在1～1.4 mm较合适。

(4)通过与单珠承载试验对比分析及高载荷验证，检验了有限元建模及算法的合理性;确定了小变形条件下阳球试件的弹塑性摩擦接触应力限额为5 384.9 MPa。

［1］陈汝训.固体火箭发动机设计与研究［M］.北京:宇航出版社，1992.

［2］张焱，孔祥安，金学松，等.轮轨三维弹塑性接触应力的算法研究［J］.力学与实践，2000，22(1):23-27.

［3］Pascoe S K.Contact stress anlysis using the finite element method［D］.Uni.Liverpool，1990.

［4］王勖成.有限单元法［M］.北京:清华大学出版社，2003.

［5］何君毅，林祥都.工程结构非线性问题的数值解法［M］.北京:国防工业出版社，1994.

［6］《合金钢》编写组.合金钢［M］.北京:机械工业出版社，1978.