基于改进Craig-Bampton法的导弹发射过程多柔体动力学研究①

高星斗，毕世华，陈 阵

(北京理工大学宇航学院，北京 100081)

0 引言

在火箭、导弹发射系统的动力学仿真中，采用多刚体动力学方法是有一定假设条件的，即假设发射系统构件变形引起的弹性位移远小于机构刚性运动和构件变形引起的弹性位移，不会影响机构运动时，常采用多刚体动力学模型分析［1］。在实际工程中，绝对刚性的物体是不存在的，各部件本身的材料和结构具有弹性，部件一方面绕惯性坐标系做运动，另一方面又相对自身局部坐标系做弹性变形运动，即部件具有柔性体特性。因此，进行动力学分析时，须考虑其弹性，从多柔体动力学角度来进行火箭、导弹发射系统动力学分析，是火箭、导弹发射虚拟样机技术研究的发展方向，具有极其重要的意义［2］。建立柔性多体火箭、导弹发射装置的数学模型对火箭、导弹发射精度有直接影响，特别是对无制导火箭弹影响更大［3－4］。

本文基于修正的 Craig-Bampton 方法［5－6］，结合多体动力学理论，建立了车载导弹垂直发射系统柔性多体动力学模型。进行了发射过程的动力学仿真，获得了导弹在发射过程中的离轨姿态参数和发射系统的动力学特性。

1 Craig-Bampton方法及其改进

1.1 传统的Craig-Bampton方法

Craig-Bampton方法将弹性结构分为若干个子结构，根据文献［5－6］推导可得子结构的模态坐标和物理坐标的变换关系:

式(1)表示通过Craig-Bampton子结构固定边界模态综合法，将弹性结构的变形用模态坐标的形式表述出来。这种结构动力学的模态分析方法是假设结构部件没有大范围刚体运动为前提的线性动力学问题(变形小于结构部件长度的10%)，在取约束模态的时候，包含子结构的刚体位移。在多体系统动力学中，部件相对于惯性系有大范围运动，结构动力学中的Craig-Bampton方法不适用于有大范围刚体运动的情况，而且Craig-Bampton子结构分析的约束模态是静态缩聚下的结果，柔性体的动态频率响应不能被反映出来，其模态不能与频率相对应［7］，难于进行结构动力学分析。因此，必须对Craig-Bampton子结构法进行改进，以满足需要。

1.2 修正的Craig-Bampton方法

求解在C-B模态坐标下子结构(单个柔性体)的动力学方程对应的无阻尼自由振动方程的特征值和特征向量:

由此获得到一个正则化模态B，原有模态坐标u可以通过新的模态坐标u*来表示:

式中 ξ*为正交的Craig-Bampton模态，具有原系统主模态和约束模态的所有特性，能够反映边界作用效应及高阶模态的拟静力作用;u*为Craig-Bampton模态坐标。

通过上述的修正后，正则化固定界面模态被无约束体的特征向量近似替代。此外，界面特征向量替代了约束模态，这样6个刚体运动模态就被去除了。

2 车载导弹垂直发射系统建模

2.1 柔性多体运动方程的建立

运用拉格朗日乘子法建立柔性多体的运动微分方程［8－9］:

2.2 刚柔耦合多体动力学方程的建立

对刚柔耦合多体系统进行动力学分析，需要把多刚体和柔性体的研究方法相结合，最终得到刚柔耦合多体系统的动力学方程。由文献［10－13］可推导用拉格朗日乘子法建立的第i个刚体或柔体的方程为

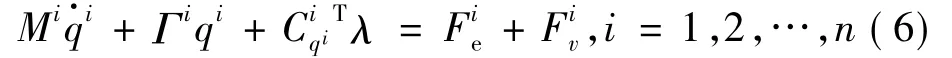
又系统的约束方程为

式(6)与式(7)联立即构成刚柔耦合多体系统的动力学方程。从中可看出，上述刚柔耦合多体系统的动力学方程从应用传统的偏微分方程解法解起来很困难。因此，应用数值解法就成为解决这个难题的主要手段。

2.3 车载导弹垂直发射系统柔性多体动力学模型

2.3.1 发射系统拓扑结构

发射系统结构示意图如图1所示，包括发射筒、导弹(数量2)、适配器、导流板、起落架、起竖油缸、支腿(数量2)、发控仓、底盘等。其中底盘通过悬挂和轮胎(数量8)及2个液压支腿支撑在地面上。为了考虑某些部分不可忽略的弹性效应，本文把车架和起落架作为柔性体来处理。

图1 车载导弹发射系统结构示意图Fig.1 Schematic diagram of vehicular missile launching system

2.3.2 柔性体模型

根据车体大梁和起落架的实际物理结构组成，在ANSYS软件平台中建立的车体大梁和起落架有限元模型如图2所示，车架共91 340个单元，25 917个节点;起落架共9 448个单元，3 724个节点。

2.4 车载导弹多柔体发射系统的建模

按照车载导弹发射系统组成结构的图纸，在三维造型软件Pro/E中把各刚体部件实体模型建好后进行装配，导入ADAMS软件中，同时把上述柔性体有限元模型也一并导入ADAMS进行装配，模型如图3所示，坐标系的定义在模型图上已给出，并约定向车头的方向看左手一侧的导弹简称为左弹，右手一侧的导弹简称为右弹。

图2 车架及起落架有限元模型Fig.2 Finite element model of the frame and undercarriage

图3 车载导弹发射系统多柔体动力学模型Fig.3 Flexible multi-body dynamic model of vehicular missile launching system

3 仿真计算及结果分析

根据图3所建立的发射系统柔性多体动力学模型，坐标系同上，进行垂直发射过程的数值仿真，仿真按2发导弹连续发射进行，并和刚性模型的计算结果进行了比较。为了获得较好的仿真结果，以便导弹发射时发射系统应处于相对稳定的状况，把发射时间定在系统仿真开始10 s之后，发射间隔定为10 s，总仿真时间26 s。图4是考虑推力偏心和阵风等气动力扰动工况下的刚、柔2种模型的初始弹道及在三维空间平面上的投影曲线(仿真取开始发射时刻到导弹完全离筒时刻为止)。

图4 刚、柔弹道和投影曲线Fig.4 Trajectory and projection of rigid and multi-flexible missiles

从刚、柔初始弹道曲线对比可看出，2种模型的初始发射弹道趋势基本一致，而在数值方面，在y方向分量上多柔体的弹道数值(最大值约13.8 mm)比刚体(最大值约0.6 mm)大一个数量级，并且由于弹性变形多柔体发射的弹道曲线呈现微小振动，这说明柔性效应不可忽略，柔性效应对初始发射弹道的影响很大，考虑多柔体效应的初始发射弹道分析很有必要也很重要。

图5是刚、柔导弹发射动力学模型在X和Y方向的角位移和角速度随时间变化的曲线。刚、柔导弹发射动力学模型发射筒筒口的角位移和角速度随时间变化的曲线如图6所示(图中曲线注释说明，例如:duorouti_zuodan_Yjiao_disp表示柔体模型左弹俯仰角位移，gangti_youdan_Xjiao_velo表示刚体模型右弹偏航角速度，其他与此类似)。

图5 导弹角位移和角速度变化曲线Fig.5 Angles and angular velocities of missiles

由图5可看出，刚、柔模型的角位移和角速度随时间变化趋势基本一致，多柔体发射模型的姿态参数偏差大于刚性模型，特别是在角速度变化方面，多柔体发射模型明显伴随着一定程度的振荡。从左、右弹方面看，右弹的扰动要大于左弹，说明导弹发射先后顺序对后续弹的离轨姿态参数有影响。但这些导弹离轨参数均在允许的制导范围内，发射系统具有较好的起控精度。

图6 发射筒筒口角位移和角速度变化曲线Fig.6 Angles and angular velocities of launch canister

由图6可看出，刚、柔模型的角位移和角速度随时间变化趋势基本一致，在数值方面，左、右筒扰动角和扰动角速度值较接近;而从刚、柔模型方面比较，多柔体模型在角速度变化方面数值上要比刚体模型扰动厉害不少，这也许是多柔体模型更接近物理实际的表现之一。

4 结论

(1)基于修正的Craig-Bampton方法实现车架、起落架子结构模型与车载导弹发射系统多体动力学模型的耦合;建立了刚柔耦合多体动力学方程，在此基础上建立了车载导弹垂直发射系统柔性多体动力学模型。

(2)车载导弹发射系统在发射导弹的过程中，发射装置的某些关键零部件的弹性变形对初始弹道性能和导弹离轨姿态参数的影响不可忽略，初始弹道在数值方面，在y方向分量上多柔体的弹道位移(最大值约13.8 mm)比刚体(最大值约0.6mm)大一个数量级。从上值可看出本文建立的车载导弹发射过程多柔体动力学模型的仿真结果相对于刚体模型更接近实际的导弹发射过程(理论值在15 mm左右)。说明本文的建模理论和仿真方法是可行有效的，相对于刚体模型，柔性多体系统的建模和分析更精确、高效。

(3)柔性仿真计算获得的初始弹道参数和刚体模型的计算结果较接近，姿态参数的变化大于刚体模型的计算结果，特别是在角速度这一扰动参数的数值上表现得非常明显，说明发射装置的某些关键部件的弹性变形对导弹发射精度的影响较大。

(4)通过仿真计算得到的刚、柔模型的初始弹道、导弹俯仰角、俯仰角速度、偏航角、偏航角速度、发射筒角位移、角速度等导弹离轨参数和发射装置扰动参数均在允许的制导范围内，发射系统具有较好的起控精度。

［1］HE Zhao-xia，LIU Geng，WU Liyan，et al.Dynamics simulation of flexible-rigid mechanism based on virtual prototyping technology［J］.Journal of System Simulation，2008，20(19):5328-5331.

［2］Beal T R，Dynamic stability of a flexible missile under constant and pulsating thrusts［J］.AIAA Journal，1965，3(3):486-494.

［3］Cochran J E ，Jr and Christensen D E.Free flight rocket attitude motion due to transverse vibration［J］.Journal of Space Craft and Rockets，1980，17(5):425-430.

［4］Cochran J E，J E Jr，T S No*and Foster W A，Jr.Dynamics of flexible missile/launcher systems［J］.AIAA Journal，1992，8(1):358-366.

［5］Craig R R，Bampton M C C.Coupling of substructures for dynamics analyses［J］.AIAA Journal，1968，6(7):1313-1319.

［6］殷学纲，陈淮，蹇开林.结构振动分析的子结构方法［M］.北京:中国铁道出版社，1991.

［7］邓峰岩，和兴锁，张娟，等.修正的Craig-Bampton方法在多体系统动力学建模中的应用［J］.机械设计，2004，21(3):41-43.

［8］黄文虎，邵成勋，等.多柔体系统动力学［M］.北京:科学出版社，1996:101-114.

［9］陆佑方.柔性多体系统动力学［M］.北京:高等教育出版社，1996.

［10］洪嘉振.多体系统动力学-理论、计算方法和应用［M］.上海:上海交通大学出版社，1992:28-65.

［11］冯勇，马大为，薛畅，等.多管火箭炮刚柔耦合多体发射动力学仿真研究［J］.兵工学报，2006，27(3):545-548.

［12］Orlandea N，Chance M A ，Calahan D A.A sparsity-oriented approach to the dynamics analysis and design of mechanical system part 1［J］.Journal of Engineering for Industry，1977，99(3):773-784.

［13］刘德贵.动力学系统数值仿真算法［M］.北京:科学出版社，2000