“事非经过不知易”的启迪

221200 江苏省睢宁高级中学(南区) 高 敏

“事非经过不知易”的启迪

221200 江苏省睢宁高级中学(南区) 高 敏

“事非经过不知难”告戒人们别把事情想得太简单，要有克服困难、战胜挫折的充分的思想准备，“凡事预则立，不预则废”嘛!若将其中的“难”字改为“易”字，就得“事非经过不知易”这个似乎“有悖常理”的说法.可笔者在多年的教学实践中却深感这种理念巨大的启迪意义和实用价值.

1 “事非经过不知易”是解题心理的“优化剂”

“事非经过不知难”揭示了解题心理的一个侧面，但事物是复杂的、多侧面的，仅仅理解了“事非经过不知难”还远远不够，还须理解“事非经过不知易”.

在各级各类试卷，特别是高考试卷中总有一定量的由于选拔人才的需要、体现区分度的所谓“难题”.这些题结构新颖、情境陌生、覆盖宽广，呈现出气势汹汹、来者不善的“大物庞然”之势.学生若信心动摇、犹疑不定、锐气消减，本来通过努力完全可以征服的题目，却一次次地痛失良机.其实解决这些问题依靠的仍然是基本的“武器弹药”，如果心理过硬、大胆进击、善于转化、据理而上、顺藤摸瓜，艰难险阻就会一步步化解.当所谓的“难题”在我们面前“俯首称臣”时，心理感觉就与先前大相径庭了：“此题也不过如此嘛!”这就是对“事非经过不知易”最生动的解读.

类似的雅俗共赏的言论还有不少，如鲁迅先生说：“世界上本没有路，走的人多了便成了路.”古语云：“千里之行，始于足下.”电视连续剧《西游记》主题曲中有“敢问路在何方?路在脚下!”民间也有虽通俗直白却含意深刻的说法：“眼是孬蛋，手是好汉”.路是人走出来的，活是人干成的.眼见任务繁重，未曾动手，先怵三分;面对路途漫长，不敢挪步，腿脚抽筋，必将一事无成.

教师须运用科学加艺术的教学手段，引领学生在解题实践中获取亲身体验，深切感悟到“事非经过不知易”的真谛，以具备无坚不摧的胆略和无题不克的气势.这样，就实现了“事非经过不知难”与“事非经过不知易”的辩证统一，最后达到的便是“事非经过也知易”的高境界.当然战略上的藐视还须战术上的重视，克“题”制胜离不开雄厚的实力，深刻理解、牢固掌握、熟练驾驭、灵活运用“双基”是成功的先决条件.基于“无知”的“无畏”只能导致乱闯瞎碰，终将“鼻青脸肿”.

2 运用“事非经过不知易”解题教学案例

教师(T)：似乎是数列，却又不是数列;涉及的是二项式的展开式，欲求值的式子前面的系数与括号中的各项都比较庞杂，“善者不来，来者不善”啊!当然最省事的办法是“放弃”!(学生笑)

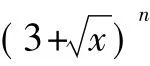
T：太好了，记得牢，抓得准!S1为我们开了一个好头，S2接着来.你说下一步该求什么?

S2：求括号中的通项，即

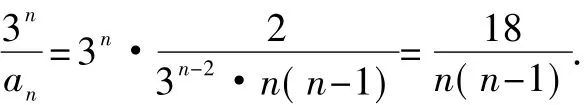
T：不能让你独享其成，请S3继续.

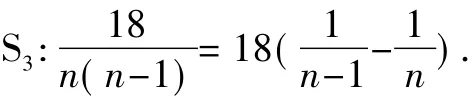
T：这么难的技巧，你也会啊?(本属于很简单的分式的拆解，教师故意反诘，学生哈哈大笑).

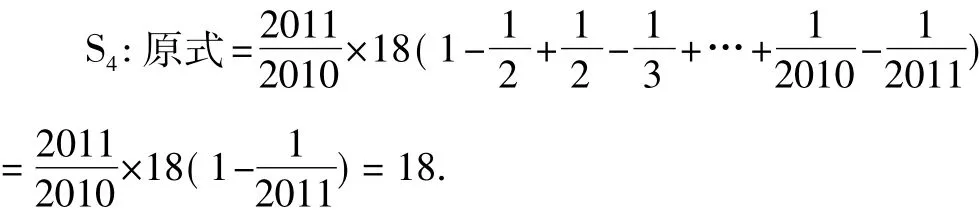
T：请大家总结成功解答此题后的真实感受.

学生的意见综合如下：题目嵌入了两个年号，很“好玩”;解答过程跌宕起伏、妙趣横生;知识覆盖面较宽;更重要的是，貌似的难题，其实不堪一击，但若缺失必要的基本功，也将无功而返.

例2 如图1，AB是平面α的斜线段，A为斜足，P是平面α内的动点，若△PAB的面积为定值，则点P的轨迹是

A.圆

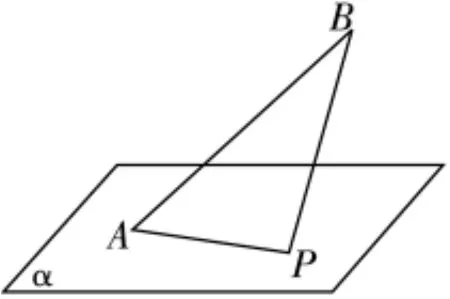
图1

B.椭圆

C.一条直线

D.两条平行线

这是某省高考试卷中的一道妙题，解答过此题的师生都感到“精妙绝伦，回味无穷”，故此题堪称高考试题中少见的佼佼者.透过简略文字和朴素图形，我们发现的是精巧的构思和丰富深邃的内涵，空间图形与动点轨迹的联袂使它呈现出扑朔迷离的浓重色彩，明眼人迅速可知决不能按通常求动点轨迹方程的思路来解答，那么从何处突破呢?

T：我是不会直接将答案奉告诸位的，只提醒题目中的关键词语“△PAB的面积为定值”.

S：AB是定值，那么△PAB的高是定值，动点P到直线AB的距离是定值.

T：抓住这“四定”就击中了此题的要害.我们知道，在平面几何中，到直线AB的距离为定值h的动点的轨迹是什么?

秦铁崖左手持铁尺，见招拆招，不管对方是什么来头，只管找准来势砍砸过去。看上去好像是笨招，但对花五奇造成的压力并不小。花五奇所怕的不是秦铁崖左手里的铁尺，而是他虚张的右手。那不是一般的手，是江湖中力道最大的分筋错骨手和龙爪手！分筋错骨手倒还罢了，龙爪手，那可是碎骨裂石的硬功夫。

S：是与直线AB的距离为定值h，且与AB平行的两条直线.

T：可这里到了空间啊!

S：以直线AB为轴旋转一周，不就行了吗!

T：说得太好了，旋转后得到什么呢?

S：得到一个圆柱面.

T：这就叫做从平面走进空间!请拿出喝水的玻璃圆柱体杯子，将它倾斜一点，这时水面的形状是什么?(如图2，学生在瞬间恍然大悟)

S：是椭圆，故选 B.

没有复杂的推理，没有繁冗的计算，没有高难的技巧，凭简单的知识和丰富的想象即可奏效.学生在灵动中思考，深深体会到只有通过实践才能真正理解“事非经过不知易”的内涵，才能在领略到此题佳妙的同时享受到成功的喜悦.

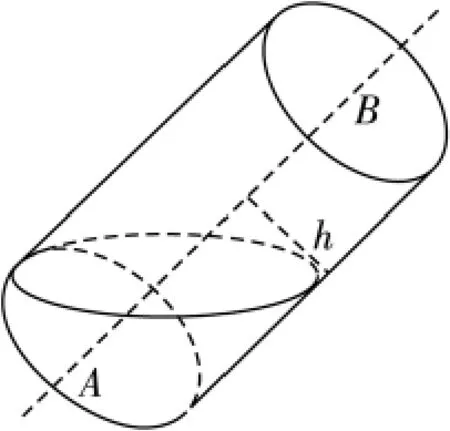
图2

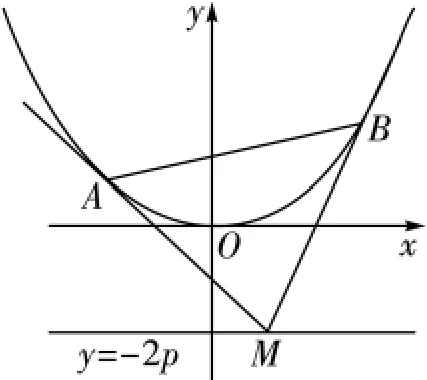
图3

T：我们之间早已有个约定，无论题目多“难”，都不说哪两个字，而要说哪两个字?

S：不说“不会”，要说“试试!”

T：结果实践试过以后才知道，此题并不难.

T：以上过程如行云流水、一帆风顺，但这是某省高考数学试卷的压轴题，不给我们制造一点麻烦和障碍，它会“善罢甘休”吗?上面两式如何处理，暂时看不到走向.请注意，要证明的是什么?

S2：要证明的是A，M，B三点的横坐标成等差数列，即x1+x2=2x0.

T：目标就是这么简单明了，但上面两式是不会轻易给你这个结果的，看来要动点“手术”.

S3：我想到韦达定理了，如果能构造出一个关于x的方程，它的两根之和为2x0，就解决了.

S4(进行紧张思考，努力寻求突破，在目标x1+x2=2x0的指引下)：将上面两个方程分别化为

由①②两式，立即知x1，x2是方程x2-2x0x-4p2=0的两根，则 x1+x2=2x0.

T：两式碰撞，智慧闪光!问题是这个技巧是否是高不可攀?

S5：以前用过这类技巧，叫做循根找方程，①②两式除字母x1，x2的下标分别为1，2外，其余的构造均相同，故称它们为同构式.

T：压轴大题也不难，奇思妙想变平凡!

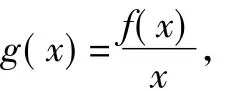
T：函数g(x)的零点就是方程g(x)=0的根，但解此方程的难度太大，用根的判别式又不可能，那么请深入挖掘知识和技能的贮存，充分调动思维的积极性，能否将方程进行转化?

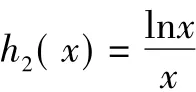
h1(x)是二次函数，其图象是开口向上的抛物线，抛物线的对称轴是直线x=e，则当x∈(0，e)时，h1(x)单调递减;当 x∈(e，+∞)时，h1(x)单调递增，h1(x)min=m-e2.

T：我们对h1(x)的认识已达到了如指掌的程度，可对h2(x)的了解还很少，怎么办?

T：真正考验我们的时刻到了，虽然我们难以画出函数h2(x)的图象，但基于对它和h1(x)的了解，为使函数g(x)有零点，必须且只需——

S：函数h1(x)与h2(x)的图象有交点.

T：好像登山，越接近山顶，山势就越陡峭，攀登的难度就越大，沉住气，憋足劲，离胜利只有一步之遥!为使函数h1(x)与h2(x)的图象有交点，必须且只需——(给学生留有必要的思考时间)

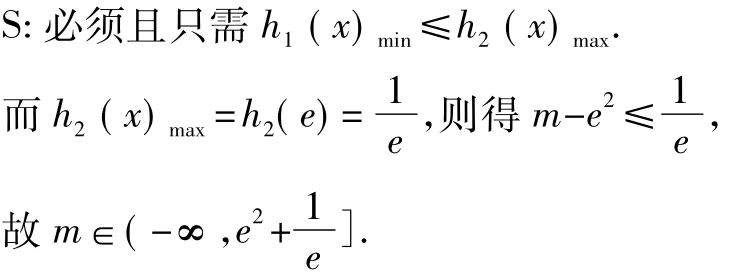
征服了似乎难以征服的困难，逾越了似乎不可逾越的障碍，取得的是空前的突破，提升的是可贵的能力，锤炼的是坚韧不拔的意志品质.回眸此类题，一种亲切感油然而生，因此要对此类题说：是你让我们的心理和思维经受了锻炼和考验，是你让我们品尝到“事非经过不知易”味道的甜美，是你让我领略到数学的奇异和美妙，是你给我们鼓足了向更高、更远的目标迈进的勇气和信心，是你让我们在征服所谓“难题”的过程中既历尽艰辛，又趣浓情深.

20110708)