对三个指数方程求解的质疑
442001 湖北省十堰市东风高中甘志国工作室 甘志国
对三个指数方程求解的质疑
442001 湖北省十堰市东风高中甘志国工作室 甘志国
求解底数与指数均有未知数的方程是有较大难度的,笔者发现一些文献求解这类方程时仅限于猜出答案,也没有注意定义域问题,所以解答不严谨.本文将分析这样的三道题目.
题1 (见专著[1]第66页的第2题)(指数方程)试解方程:xx2-1=3.(提出人:广东大埔高陂方丁)


下面再给出题1的推广问题的若干结论.

定理2 若a是已知的正实数,则方程xx2-1=a(x>0)的全部解是:
(1)当0<a<1 时,无解;
(2)当a=1时,解集是{1};

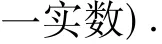
问题 请读者找出方程xx2-1=a(x∈R)有四个解的例子.
题2 (一团漆黑)试解方程xx=x.
这里面连一个已知数都没有,不是一团漆黑吗?
该书第204页给出的解答是:
用两端取对数的方法来解这个方程
xlgx=lgx,(x-1)lgx=0,
所以x=1,
经检验知x=1是原方程的根.
奇怪的是x=-1也是原方程的根,可是它不能通过解方程的正常途径而得到.
(见专著[2]第160页)
该解答体现了趣味性,但不是完整的解答.
文献[3]用较长篇幅求出了方程xx=x的所有实数解只有两个:x=±1.专著[4]也给出了该方程所有实数解的简洁求法,下面再给出两种简解(只须再求x<0的解):

再由已得的结论方程 tt=t的正数解是 t=1,得-x=1,x=-1.
题3 (解指数方程组)试解联立方程式:x+y=5,xy+yx=17.(提出人:杨擎天)
解 由第一式得出y=5-x,代入第二式就有x5-x+(5-x)x=17.
令s=x5-x+(5-x)x,当x,y都只允许取实数的时候,要s的值等于17,就可以看出x与y都是有界的.如果把x=8代入s的表示式就有s>17,这就表明x只能小于8才可能满足所给的两个方程.
又因为x与y互换,原方程式是不变的,经过试验可以得出x=2,y=3与x=3,y=2是原方程组的2解.
(见专著[1]第2页的第2题)
对于题2,其解答有以下不严谨之处:
(1)看不出x与y都是有界的.
设s(x)=x5-x+(5-x)x,由s(8)>17不易得出“s(x)<s(8)⇒x<8”,因为不易证得函数 s(x)在x<8时是增函数(事实上,s(6)>s(7)).
(2)由“x与y互换原方程式是不变的”,只能得到“若(x,y)=(x0,y0)是原方程组的一组解,则(x,y)=(y0,x0)也是原方程组的一组解”,但难以得出原方程组的所有实数解是(x,y)=(2,3),(3,2).
笔者认为,完整解答此题是有难度的.
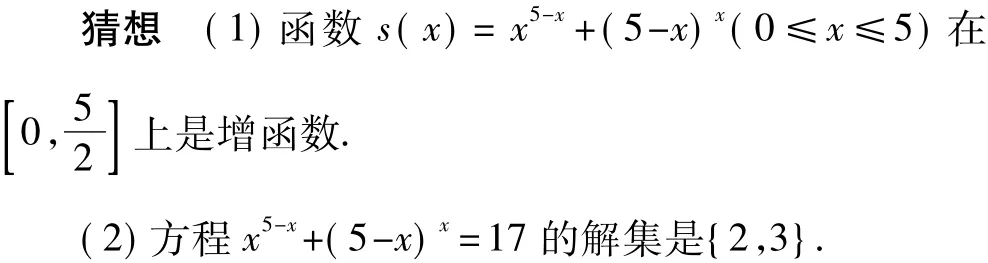
1 刘培杰主编.400个中国最佳初等数学征解老问题[M].哈尔滨:哈尔滨工业大学出版社,2009
2 谈祥柏,杨京玉.趣味代数300题[M].北京:中国青年出版社,1998
3 芝原,赵慈庚主编.指数方程xx=x的解法.初等数学研究[C].北京:北京师范大学出版社,1990
4 甘志国著.初等数学研究(I)[M].哈尔滨:哈尔滨工业大学出版社,2008
20110811)

