基于水声信号的瞬时频率估计算法

张 靖

(大连测控技术研究所,辽宁 大连 116013)

0 序言

在许多实际的信号处理应用中,估计一个非平稳时变过程的瞬时频率(Instantaneous Frequency,IF)意义重大。一些信息探测系统只要系统与目标之间有相对运动,就会产生“多普勒效应”,频率会随相对运动发生变化,传播媒质的扰动也会使频率变化,雷达、声呐、移动通信、医疗设备和天文观测等都存在这一问题。

目前针对瞬时频率的估计方法的核心为概论统计,统计中所用的统计量,主要是样本平均值或样本函数算数平均值,它们具有最小方差性、无偏性等相当好的特性。然而样本平均值的抗干扰性很差。为了获得稳健统计解,发展了一种既保留所有数据,又削弱污染源对统计结果影响的统计方法,即 M-估计[1],其能获得稳健性的瞬时频率估计值。

目前对瞬时频率的估计方法有很多,对于水声信号受海洋声场环境非常复杂、测量测备工作状态不稳定、信噪比不足等因素的影响,很难获得理想的瞬时频率特征[2-5]。对于随时间呈线性变化的非平稳信号来说,其稳健的瞬时频率估计是必要的。研究分析水声信号的瞬时频率估计方法对实船噪声特征频率提取,辐射噪声“多普勒效应”分析及噪声源分析意义重大。本文提出一种综合相位法和M估计方法获得水声信号的瞬时频率,并利用计算机仿真分析研究该方法的效果。

1 相位差分方法

对于理想的信号,其离散水声信号可以表示成r(n)=Aexp[jφ(n)]。

根据离散信息瞬时频率定义,离散时间域对应为差分运算,即可得到离散时间瞬时频率的估计。有3种相位差分算子[6],它们分别是前向有限差分、后向有限差分和中心有限差分,与这3种相位差分算子相对应的瞬时频率估计见式(1)～式(3)。

当信噪比很高时,利用中心差分法直接估计某特征频率的瞬时频率,得到的频移特征曲线较平滑,误差较小,精度高。

由于水声信号容易受到干扰,单纯地采用时刻Ti-1和Ti+1的相位估计Ti时刻的瞬时频率,由于相位离散度大引起的瞬时频率估计误差也很大,很难准确估计瞬时频率。由于通过较长的平均时间可以有效地抑制噪声的影响,因为当噪声服从高斯分布时,噪声方差将随着平均时间的增加而线性减小。因此在低信噪比情况下,增加有效观测时间是提高同步性能的方法之一,从而采用长时间多点相位中心差分法。

根据Tayker公式可得:

针对离散相位信息,分别取 Δ t=i,i+1;t=n0,则可得

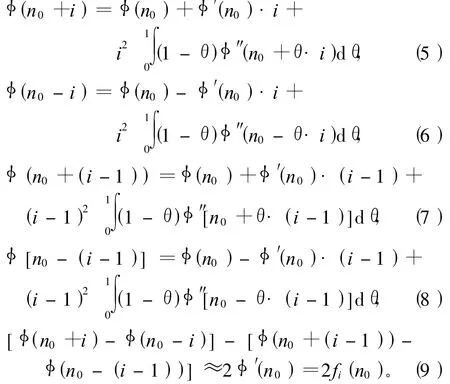
因此可近似得到 1组 2f1(n0),2f2(n0),…,2fi(n0)。

2 基于M-估计方法分析瞬时频率

对于M-估计方法,核心是在稳健性和精确性的2个定量化泛函空间中,找出1个鞍点,即敏感性最差、精确性最好的解[6]。实际是取函数 ψ(x),解方程

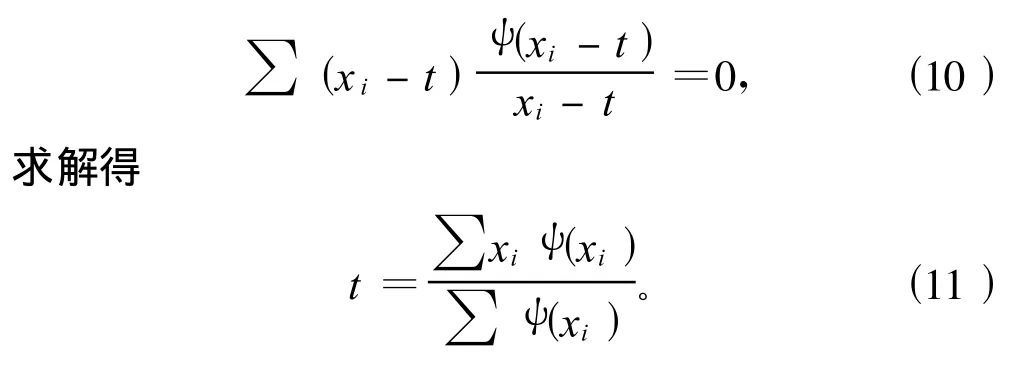
令wi=,则上式刚好写成加权平均的形式t=∑xiwi,即形成自动加权的权函数平均形式。

通过求解方程可知,当满足tn=tn-1时,tn-1为最优解。

依据估计准则的统计背景,M-估计可以分为3类[7]:一是基于概率密度(或误差分布)的M估计,如最小二乘估计等;二是与概率密度无关的M估计(经验方法),权函数通过数值模拟获得,而无须顾及是否知道误差的概率密度,如丹麦法等;三是基于随机模型验后估计的稳健估计,如李德仁选权迭代法。在参数回归估计中,不同的权函数形式产生了不同的估计方法。为了实现参数估计的稳健性,一般遵循大误差以小权,小误差以大权,等价权公式可以通过数值模拟经验确定的原则。等价权是残差的函数,参数的迭代求解中残差的改变引起等价权的改变。本文采用的权函数[8]为:

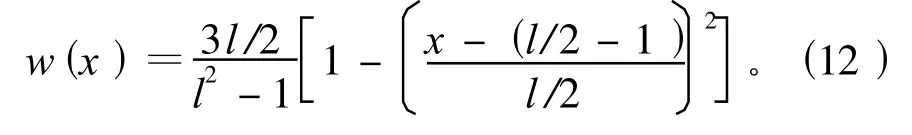
3 仿真分析

本文通过仿真模拟不同信噪比下水下目标匀速直线运动产生的单频线谱辐射噪声,分析其由于多普勒效应产生的瞬时频率特征。

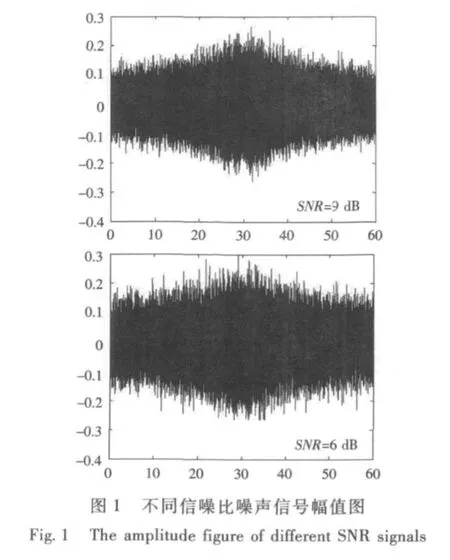
仿真数据:信噪比分别为6 dB和9 dB;信号频率100 Hz;采样时间60 s;目标速度6 m/s;目标最近距离30 m;其建立的仿真信号如图1所示。

对仿真建立的信号分别采用不同长度的权函数进行分析,其结果如图2和图3所示。

通过上图可以看出,对于同1组噪声信号,权函数的长度越长,其瞬时频率估计值越接近真值;对比不同信噪比的噪声信号,采用相同权函数长度分析情况下,信噪比越高,瞬时频率估计值越理想。同时应该指出,该方法权函数长度越长,要求的噪声数据量越大,因此计算量大耗时较长,一般适合对信号的后续分析,不适合对信号的实时跟踪。

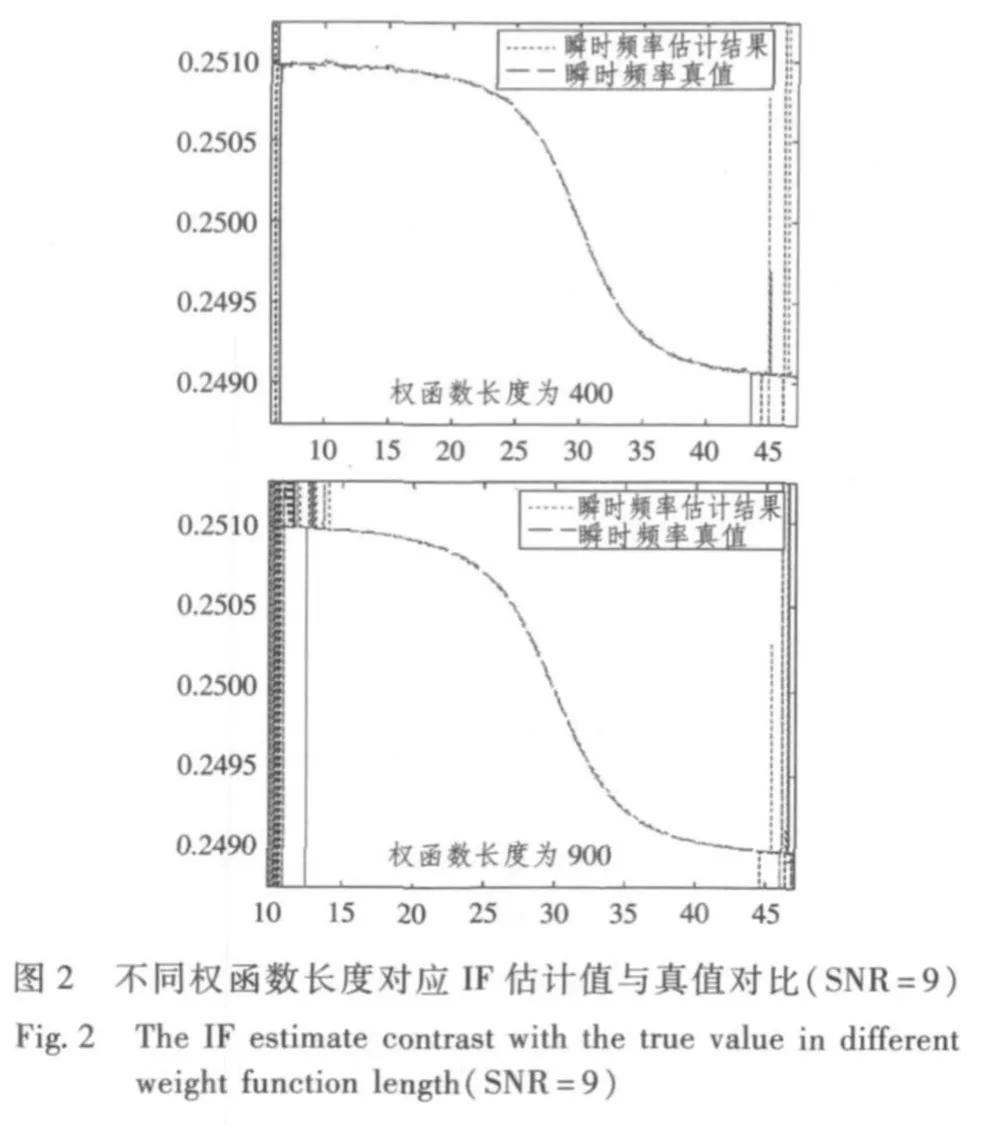
4 结 语

本文通过研究建立了一种稳健的瞬时频率估计方法,通过计算机仿真分析,研究了不同信噪比、不同权函数长度对瞬时频率估计的影响。综合分析表明,该方法能有效的估计运动目标速度较低情况下产生的瞬时频率。

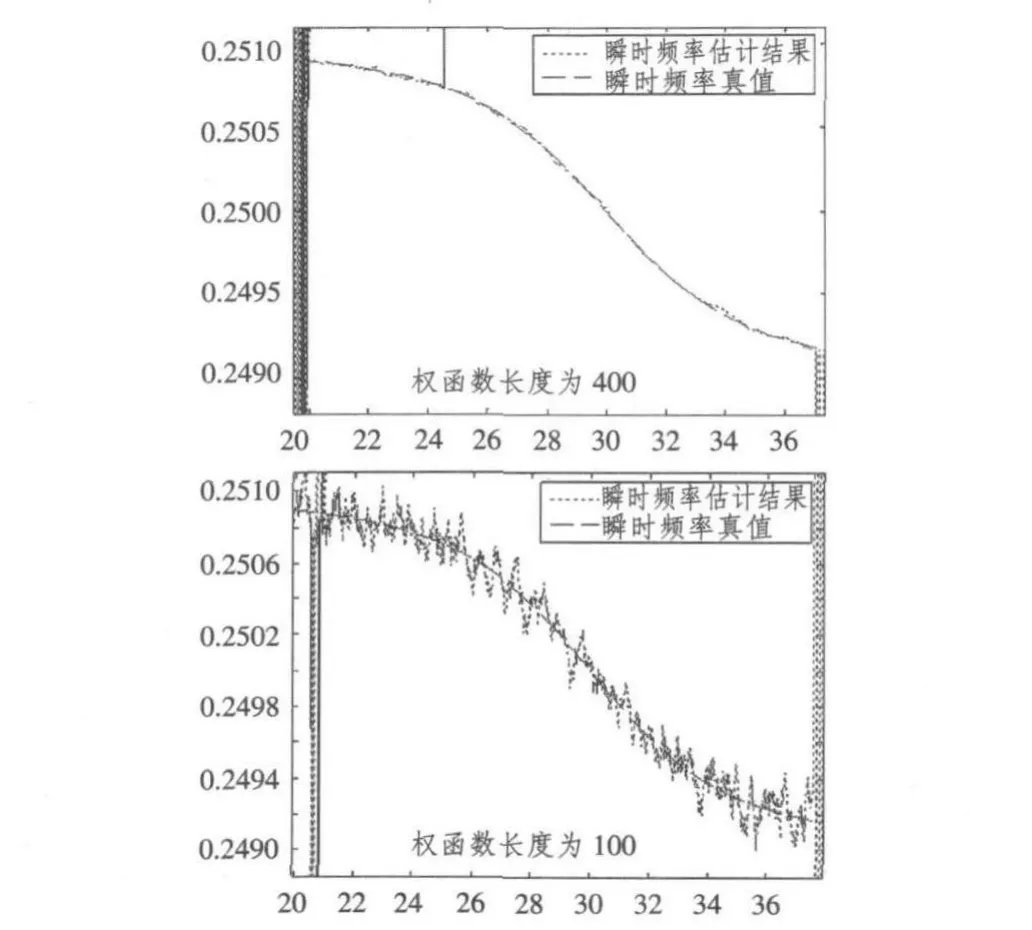
图3 不同权函数长度对应IF估计值与真值对比(SNR=6)Fig.3 The IF estimate contrast with the true value in different weight function length(SNR=6)

[1]王安帮,等.M-估计的权函数选取及其抗差性比较[J].北京测绘,2008,10(1):8-10.WANG An-bang,et al.Selection of M-estimated weight functions and robust comparision[J].Beijing Surveying and Mapping.2008,10(1):8-10.

[2]李红娟,孙超.水声通信自适应多普勒频移补偿仿真研究[J].计算机仿真,2007,24(2):302-304.LI Hong-juan,SUN Chao.Adaptive doppler compensation forunderwateracousticcommunication[J].Computer Simulation,2007,24(2):302-304.

[3]李君桥,等.基于多普勒频移的水下运动目标测距技术[J].声学技术,2008,27(5):758-760.LI Jun-qiao,et al.Passive ranging of underwater motional targets based on Doppler frequency shift[J].Technical Acoustics,2008,27(5):758-760.

[4]庄晓明,等.基于多普勒频移的水下超声探测目标回波信号处理方法[J].舰船电子对抗,2008,31(6):88-91.

[5]DJURIC P M,KAY S M.Parameter estimation of chirp signals[J].IEEE Transactions on Acoustics,Speech and Signal Pro2 cessing,1990,38(12):2118-2126.

[6]孙晓奇.非平稳信号瞬时频率估计[D].硕士论文,2009.

[7]王文军.极大似然估计的稳健改进[J].武汉工业学院学报,1990,(4):35-41.

[8]黄晓红,等.改进的相位展开算法及其在瞬时频率估计中的应用[J].电子学报,2009,(10):2266-2272.