三序节点导纳矩阵在工程中的程序实现

张洪波 付小鹏

（1.河南省电力公司培训中心，郑州 450052；2.煤炭工业郑州设计研究院有限公司，郑州 450007）

电力网络的数学模型是现代电力系统分析的基础，电力网络通常是由相应的节点导纳矩阵或节点阻抗矩阵来描述的。在电力系统分析中，我们需要面对成千上万个节点及电力网络所连接的电力系统，因此，对电力网络的描述和处理往往成为解决问题的关键[1-2]。

以阻抗矩阵为基础的节点方程可以由注入电流直接求出电力网络各节点的电压，曾在电力系统计算中获得广泛应用。但由于节点阻抗矩阵是满矩阵，其存储规模及形成所需的计算量都随电网规模增大而呈平方增加，要求计算机有较大的内存容量，同时也增加了运算次数，降低了计算速度，因而当系统规模变大时，节点阻抗矩阵的应用受到一定限制；而电力网络的节点导纳矩阵具有良好的稀疏特性，其存储规模和计算量一般与电网的规模呈线性关系，通过稀疏技术的引入，计算速度相比于阻抗矩阵模型大幅度降低，同时考虑到节点导纳矩阵在处理复杂电网结构和复杂故障方面的灵活性，可以高效地处理电力网络方程，因此是电力系统分析中广泛应用的数学模型[3]。

1 节点导纳矩阵的程序实现

节点导纳矩阵是用来描述电力系统网络模型的最基本的矩阵，由网络的结构和网络元件的参数决定。它是电力系统分析计算及相关高级应用软件的计算基础，因此，导纳矩阵的正确与否对电力系统分析计算及相关高级应用软件的计算结果准确性有着举足轻重的意义[4]。

通过扫描网络中的支路，并根据支路在网络中的连接关系直接形成自导纳和互导纳，由于节点导纳矩阵为稀疏矩阵且是对称矩阵，可以利用稀疏矩阵技术进行存储，只存储导纳矩阵的上三角部分。节点导纳矩阵的程序实现如图1所示。图中的YII、YIJ数组分别用来存放各节点的自导纳和互导纳；NYseq数组按导纳矩阵行号顺序存放各行非对角元素的首地址；NYsum数组用来存放导纳矩阵中各行非对角元素的个数。支路状态属性0代表停运，在计算中不考虑；1代表线路支路；2代表YN/Yn接法的变压器；3代表YN/d且运行的变压器或其他接法的变压器；4代表对地支路；5代表发电机支路；6代表Yn/d接法且停运的变压器。其中，支路状态为3和6的支路计算时比较特殊，其正、负序导纳矩阵和零序导纳矩阵的形成不同。实际上，在零序网络中，YN/d接线的变压器支路的零序导纳只对YN侧节点的自导纳有影响，也就是YN/d变压器相当于一条对地支路。对于支路状态为6的支路在正、负序导纳矩阵计算中由于处于停运状态不进行计算，但在零序导纳矩阵计算中却要考虑。

图1 节点导纳矩阵的程序实现

2 节点导纳矩阵计算中应注意的问题

2.1 三序网络节点和支路编号

当电力系统处于不对称状态下，会出现正序、负序和零序分量，此时电力网络方程就是三序网络方程。三序网络方程是正序网络、负序网络、零序网络以及它们之间相互关系的电气特性的数学描述，它是电力系统分析和计算的理论基础。三序网络方程的系数矩阵就是三序导纳矩阵。因此，三序网络分析是导纳矩阵的计算的前提。

对于正序网和负序网，其网络结构相同，只是在计及发电机和负荷阻抗时，正序和负序导纳矩阵的对角元素不相同而已；对于正序网和零序网，其不同之处有两点：一是零序参数不同于正序参数，二是由于零序网络与变压器绕组接线方式和中性点接地方式有密切的关系，网络结构与正序网存在较大差异，零序网络通常比正序网规模小，因此，存在序网间节点和支路编号不对应问题[5-6]。

为了解决这个问题，通常有两种解决方法：一种是正序网和零序网的编号各自独立进行，在编号完成后建立序间节点、支路编号的检索，节省储存零序导纳矩阵的内存开销，但由于正序网和零序网节点号不同，会给计算带来许多麻烦；一种是零序网采用与正序网完全一致的编号，这样，零序网络会出现一些空节点，即不连接任何支路的节点，在编写网络方程求解程序时，应增加判别空节点的功能，避免运算出错。

2.2 含YN/d接线方式变压器在零序导纳矩阵计算中的处理

在电力网络拓扑分析时，根据电网中各设备之间的连接关系将设备模型处理为两类：节点类和支路类，通常将网络中的输电线路、变压器和对地支路统称为支路。输电线路及对地支路在正序、负序和零序网络结构中是相同的，但变压器在三序网络结构中却受自身接线方式和中性点接地方式的影响。

文中采用的网络模型中支路类包含以下属性[7]：首节点编号、末节点编号、支路状态、支路正序、负序、零序阻抗，其中支路状态中 0代表停运，1代表投运的线路， 2为YN/yn接线的变压器，3为YN/d接线的变压器，其他接线的变压器填2或3均可，但零序阻抗为 0。通过在实际中的应用发现，变压器支路的状态属性用0、2、3这三种状态表示还不完全。如图2（a）所示的简单网络，按照各设备元件的正序、零序阻抗的等值电路分析[8]，其正序、零序网络结构如图 2（b，c）所示。以图中的变压器T4为例，对于 YN/yn/d接线方式的变压器可以等效为三个YN/yn，YN/yn，YN/d接线方式的双绕组变压器，若 T43支路处于停运状态，将该支路的状态属性中置为 0，此时形成的正序网络会有所改变，如图 3，而零序网络不变。按照上述计算导纳矩阵的方法，在形成零序网络时，在判断支路状态为0时，将停运支路剔除，因此，对于节点4会少计算一条支路形成的自导纳，造成零序导纳矩阵计算的不准确。为了解决这个问题，为此，在进行网络分析形成支路类数据时，对于变压器的支路状态描述只有0、2、3三种状态是不够的，需要新增一个状态类型代表该支路为 YN/d接线方式的变压器且处于停运状态。这样在形成节点导纳矩阵时，通过判断支路的状态属性就不会造成支路丢失，保证计算的正确性。

2.3 两节点间多回线路的处理

在实际电网模型中，常常存在两节点间有多回线路相连的情况，手工计算时可以轻易的找出两节点间的多回线路，而在计算机程序实现过程中，需要通过比较电网支路模型的首、末节点属性来判断是否为多回线路。当为多回线路时，首、末节点的自导纳及首末节点间的互导纳需要修改，但在统计节点导纳矩阵对应行的非对角元个数时需要注意，由于多回线路只是影响自导纳和互导纳的计算，并没有造成非对角元个数的增加，因此，在程序中当判断存在多回线路时，NYsum数组中对应该行的非对角元个数不增加。

3 实例

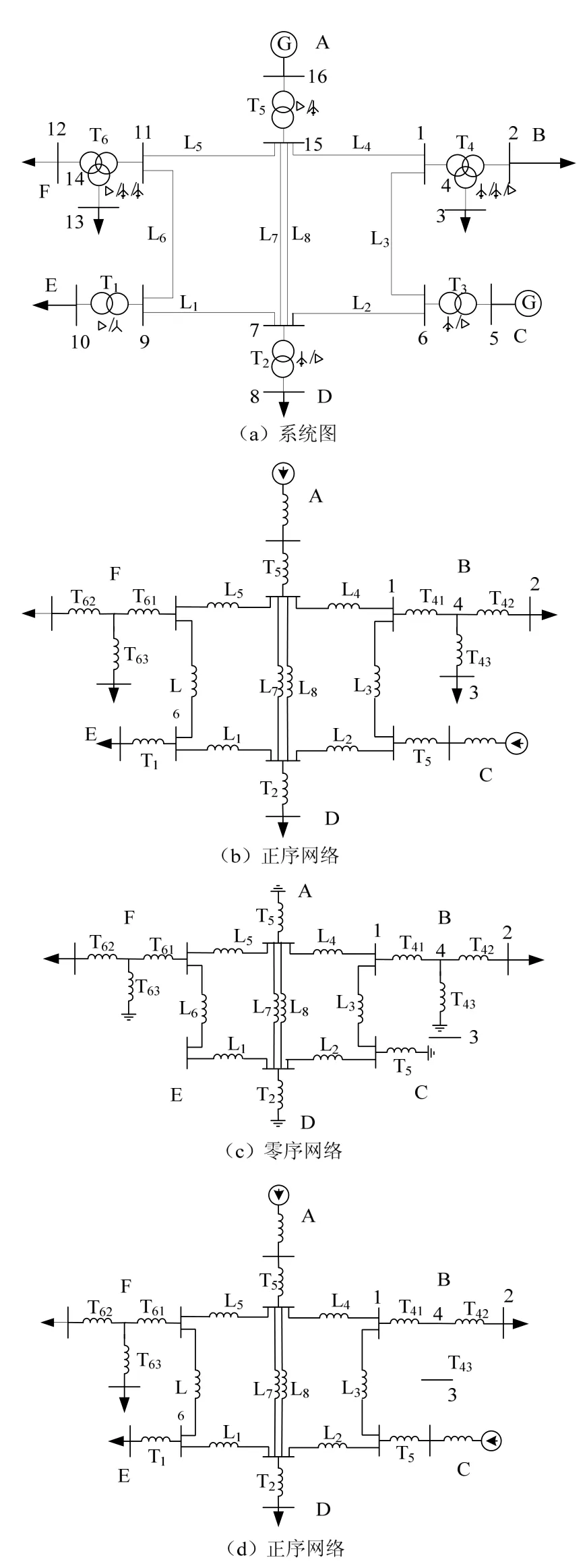
图2 序网图

如图2（a）所示的网络，各元件的参数如下（各参数均为标幺值，100MVA为基准值）：线路 L1：正序电抗=j0.0343，零序电抗=j0.0796；线路L2：正序电抗=j0.255，零序电抗=j0.0591；线路L3：正序电抗=j0.218，零序电抗=j0.6407；线路L4：正序电抗=j0.178，零序电抗=j0.5304；线路L5：正序电抗=j0.19，零序电抗=j0.5658；线路 L6：正序电抗=j0.0131，零序电抗=j0.03768；线路L7：正序电抗=j0.037，零序电抗=j0.113；线路 L8：正序电抗=j0.037，零序电抗=j0.113；变压器 T1：正序电抗=j0.0217，零序电抗=j0.0503；变压器T2：正序电抗=j0.064，零序电抗=j0.134；变压器 T3：正序电抗=j0.0124，零序电抗=j0.049；变压器T5：正序电抗=j0.0124，零序电抗=j0.049；变压器T4：正序电抗分别为 j0.018，-j0.002，j0.0553，零序电抗分别为j0.018，-j0.002，j0.0553；变压器 T6：正序电抗分别为j0.01，j0.001，j0.0337，零序电抗分别为j0.01，j0.001，j0.0337；发电机A：正序电抗=j0.15，零序电抗=j0.05；发电机 C：正序电抗=j0.075；零序电抗=j0.025。其中，各元件的负序参数与正序参数相同。通过程序计算得出的结果如下表1－3。

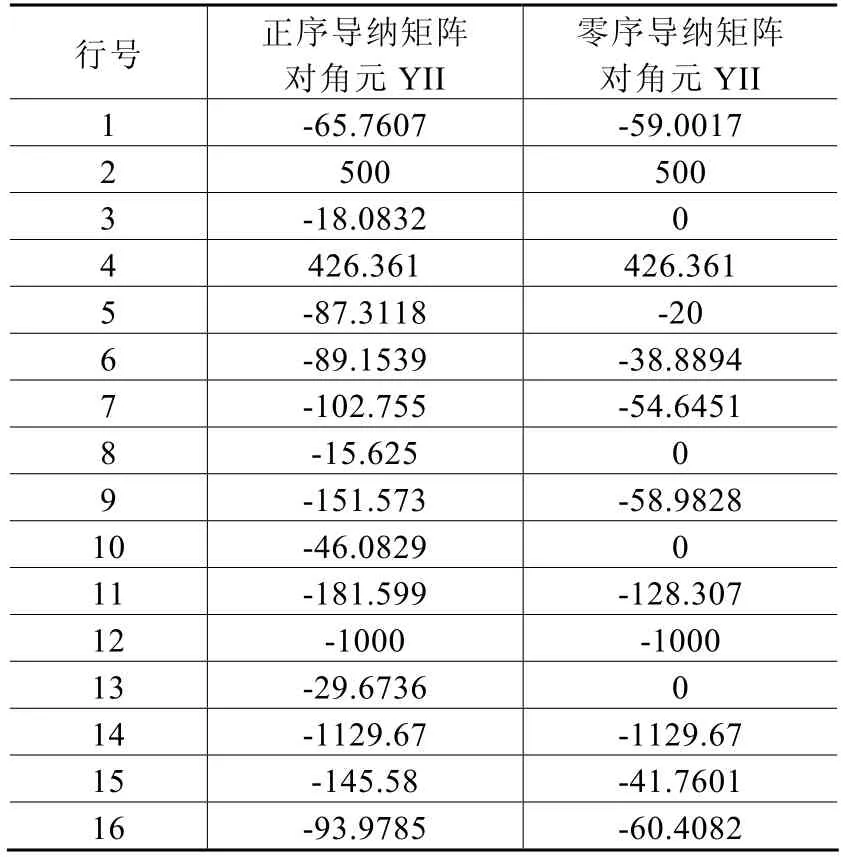
表1 导纳矩阵对角元

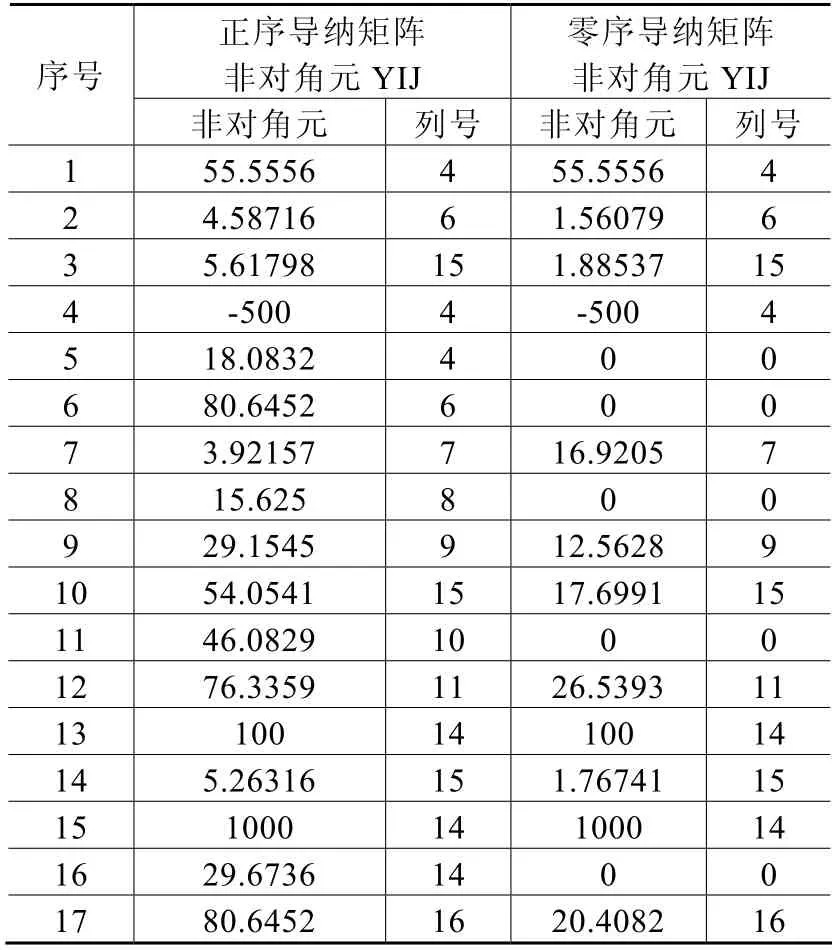
表2 导纳矩阵非对角元

表3 数组NYsum、NYseq

4 结论

节点导纳矩阵作为电力系统分析计算中广泛应用的数学模型，其计算结果的正确性有着举足轻重的意义。根据在多个实际工程中的应用，发现三序节点导纳矩阵计算中应注意的问题，通过对这些问题的分析，提出了一种实用化的节点导纳矩阵的程序实现方法。经过多次的验证，该程序能够正确的计算电网的节点导纳矩阵，为电力系统分析计算做好基础。

[1]张伯明,陈寿孙,严正.高等电力网络分析[M].北京:清华大学出版社,2007,9.

[2]西安交通大学等.电力系统计算[M].北京:水电出版社,1978.

[3]王锡凡.现代电力系统分析[M].北京:科学出版社,2003.

[4] 于尔铿,刘广一,周京阳,等.能量管理系统[M].北京:科学出版社,2001.

[5]陈冬,吕飞鹏,刘洋,雷云川,谢熹.基于MS.NET的电力系统序网络拓扑分析[J].电气应用,2007,26(11):21-15.

[6]陈亚民.电力系统计算程序及其实现[M].北京:中国电力出版社,1995.

[7]吴晨曦,盛四清.电力系统短路计算数据的生成[J].2003,23(11):63-65.

[8]李光琦.电力系统暂态分析[M].北京:中国电力出版社,1995,5.