一类欠驱动系统的控制方法综述

孙宁，方勇纯

(南开大学机器人与信息自动化研究所，天津 300071)

一类欠驱动系统的控制方法综述

孙宁，方勇纯

(南开大学机器人与信息自动化研究所，天津 300071)

近年来欠驱动系统已经成为机器人与自动控制领域的研究热点之一，本文对一类欠驱动系统(欠驱动连杆系统)的控制方法的研究状况进行了综述.首先给出了欠驱动系统的动力学模型，并介绍了2种基本控制模式;随后，对其主要的控制方法，包括最优控制方法、运动规划法、部分反馈线性化方法、能量(无源)方法、变量降维法、分级控制设计方法及智能控制方法，展开了分析与讨论;在此基础之上，对欠驱动连杆控制系统设计存在的抗干扰性、实用性及快速性等主要问题进行了简要分析，并就今后的研究方向进行了展望，如鲁棒策略、饱和控制与有限时间控制等.

欠驱动系统;机器人;智能控制

所谓欠驱动系统，是指独立的控制输入维数少于系统自由度的一类系统，其本质为非线性系统.在现实中的很多系统都被设计为欠驱动形式，主要是因为:1)系统本身的运动受到某种约束，如常见的非完整约束;2)省去部分驱动器后，一方面可以减少设计的复杂程度，提高系统的灵活性，另一方面可有效节约成本，降低系统自身的重量与体积，并减少能耗.根据上述2种不同的原因，可以将欠驱动系统大致分为2类:第一类是运动受限欠驱动系统［1］，如移动机器人、航天飞行器、欠驱动水面和水下航行器等，该类系统由于受到非完整约束等的影响，无法完成侧移等运动;另一类欠驱动系统，主要包括各种起重机［2］(桥式起重机、臂式起重机、塔式起重机)、倒立摆系统［3］、Furuta pendulum［4］、球棒(ball and beam) 系统［5］、TORA(translational oscillator with a rotating actuator)系统［6］、以及 Acrobot(Acrobat robot)［7］、Pendubot(pendulum robot)［8］等欠驱动机械臂，它们的系统状态可看作“连杆”的平移(如倒立摆、起重机中的小车与球棒系统中的滑块等的运动)或旋转(如Acrobot和Pendubot等系统中的旋转臂的转动)，都具有相似的动力学性质，且控制方法非常类似，基于此，不妨将它们统一归类为欠驱动连杆系统.上述2类欠驱动系统在动力学模型、控制模式与控制方法等方面明显不同，在本文中，将主要综述欠驱动连杆系统的研究情况.

欠驱动特性给系统的设计与制造带来了很大的方便，但是它往往会导致系统内部的动力学特性比全驱动系统更加复杂，并使得系统状态之间相互耦合或伴随非完整约束，这些都给其控制带来了巨大的挑战.研究欠驱动系统不仅有着重要的理论意义，可以推动自动控制理论，尤其是非线性控制理论的发展，而且具有重大的实际应用价值，例如当全驱动系统的部分驱动器失效时，它们就相应地变成欠驱动系统，此时，欠驱动控制算法可作为应急控制策略以保证系统仍然能正常运行.值得指出的是，尽管倒立摆、球棒系统等基准系统是专门为教学研究及验证不同的控制算法而设计的;但它们无一不来源于现实中某些复杂系统的运动模型，因此对其进行深入研究的意义深远.正是由于这些原因，连杆类欠驱动系统的控制已经成为国内外自动控制及机器人领域最热门的研究方向之一.

本文对欠驱动连杆系统的研究现状进行了综述，重点分析了近年来针对这类系统提出的主要控制方法，以及获得的研究结果，并对有待进一步解决的问题及未来的研究方向进行了讨论与展望.

1 动力学模型与控制模式

1.1 动力学模型与性质

建立准确的动力学模型，是对系统进行动态分析与完成高性能控制器设计的保证.由于欠驱动连杆系统具有多变量、强耦合的性质，借助传统的牛顿力学分析方法为其建立准确的模型非常困难.相比之下，欧拉－拉格朗日(Euler－Lagrange)法则可以通过计算系统的能量，方便地得到系统的动力学模型，因此被广泛地应用于复杂欠驱动系统的建模.经建模后，自由度为n，独立控制量个数为m(m ＜n)的欠驱动连杆系统的动力学模型具有如下统一的矩阵形式［3－9］:

式中:q∈Rn×1为系统状态向量;M(q)∈Rn×r为惯量矩阵;V(q，)∈Rn×n为向心－柯氏力矩阵;G(q)∈Rn×1为重力因子向量;U∈Rn×1为控制向量，具体表示为

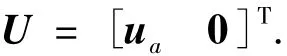
式中，ua∈Rn×1为驱动向量.为了更加直观地体现系统的欠驱动特性，可将动力学模型(1)进一步改写为

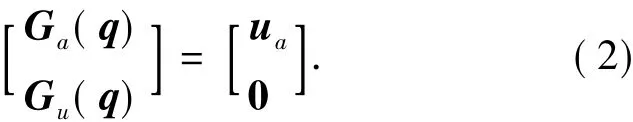
式中，各个变量分别对应于式(1)中相应矩阵或向量的分块，下标a与u分别表示驱动环节与欠驱动环节.特别地，将式(2)中的欠驱动部分单列如下:

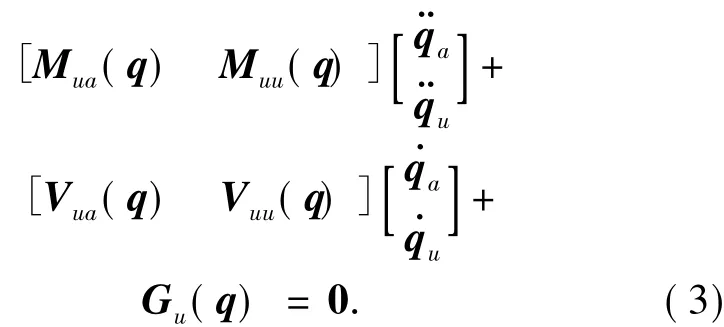
式(3)是欠驱动连杆系统的运动学模型，它体现了系统可驱动状态与不可驱动状态之间的动态耦合关系.因此，它是对欠驱动状态进行间接控制的前提和保障.

性质1M(q)为正定对称矩阵.

性质2(q)/2－V(q，)是斜对称矩阵.

这2条性质被广泛地应用于欠驱动连杆系统的控制器设计与稳定性分析.

1.2 控制模式

根据控制目标的不同，欠驱动连杆系统的控制模式可分为镇定控制(regulation control)与轨迹跟踪控制(trajectory tracking control)2种.

镇定控制又称点镇定控制，是指设计一定的控制律，将系统从某一初始状态镇定到特定的期望状态(一般是平衡点)，并使得系统在该状态保持稳定.镇定控制模式被广泛地应用于各种欠驱动连杆系统.以二维桥式起重机系统为例，其系统状态为台车的水平位移和负载的摆角，而控制量为作用在台车水平方向上的驱动力，其镇定控制主要考虑如下指标:一方面，台车应尽可能快地到达目标位置，以保证负载的传送效率;另一方面，在传送过程中负载摆角应尽可能小，在台车到达目的地后摆角应迅速衰减为零，以避免负载与周围物体发生碰撞，提高系统的安全性和运送效率.类似地，倒立摆、Acrobot、Pendubot等的摇起(swing up) 控制［3，7－8］及球棒系统的平衡(balance)控制［5］也属于镇定控制.

相应地，轨迹跟踪控制则是指设计一定的控制信号，使得系统状态沿设定的轨迹稳定运行.在这里，轨迹是指系统状态位置、速度和加速度随时间变化的集合，而非仅仅是空间中的一条与时间无关的路径.合理的轨迹规划不仅可使欠驱动自由度按照一定的规律运动［4，10］，而且可以有效地提高系统的运行效率［11－12］.然而，由于欠驱动连杆系统的轨迹生成必须满足动态约束关系(3)，即该类系统缺乏跟踪空间任意轨迹的能力，因此其轨迹规划与全驱动系统相比更具有挑战性.

2 控制方法及研究现状

由于缺少部分驱动器，欠驱动系统不能实现完全反馈线性化，从而导致全驱动系统控制中的许多控制策略都不再适用.因此，如何对欠驱动连杆系统实施有效控制一直以来都是一个开放性的问题，国内外相关领域的研究人员对其进行了深入研究，并取得了许多成功的研究成果.在本节，将对主要的控制方法及其研究现状进行综合分析.

2.1 最优控制方法

一般而言，最优控制是指分析系统的模型和控制要求，通过构造某个指标函数来设计控制器使系统性能达到最优.然而，由于欠驱动连杆系统中存在不可驱动的状态/输出，在构造指标函数和设计控制算法时只能包括部分性能，或者折衷考虑控制要求，而无法使所有控制指标同时实现最优.如对于起重机而言，台车的快速运动和负载摆动的抑制相互冲突，在设计最优控制律时只能考虑其中一个方面，或者把两者进行组合之后提出一个新的控制目标来设计控制器.为此，Y.Sakawa等人针对线性化的模型设计了摆角最优控制律，但该方法牺牲了系统整体的运送效率［13］;J.Auernig等从系统的工作效率出发，充分考虑了台车的最大运行速度等限制，借助庞特里亚金(Pontryagin)极大值原理实现了最小时间控制，但却难以控制负载传送过程中摆角幅值的大小［14］;而在文献［15］中，K.Terashima等人首先建立了臂式起重机在三维空间中的直线传输模型，然后借助非线性最优设计方法实现了负载的时间最优传输，并较好地消除了负载的摆动，遗憾的是，该策略同样未能将负载的摆动性能引入最优控制器的设计.欠驱动系统不仅无法使全部性能指标同时达到最优，而且其强耦合、非线性特性也为获得最优控制输入的解析解(甚至是数值解)增加了很大的难度.为此，可以在求解最优约束时对目标进行适当的变换，如针对Furuta pendulum系统，文献［16］将其有界输入下的时间最优控制问题巧妙地转换为在不超过输入极限的前提下如何保证时间最短的问题，并通过非线性优化得到了数值解，从而成功地解决了该类欠驱动系统的非线性最优控制问题.

2.2 运动规划法

运动规划是指为系统状态/输出规划一条合理的运行轨迹，使得当系统沿该轨迹运行时能实现特定的功能.它主要适用于平衡点自然稳定的连杆系统，如各种起重机，该方法主要包括离线轨迹规划［17－19］和输入整形 2 种［20－25］.

以桥式起重机为例，离线轨迹规划方法主要通过分析台车与负载之间的动态耦合关系来规划台车的运行轨迹，为此既要保证台车快速准确定位，又要对负载摆动(尤其是残余摆动)进行有效抑制.孙宁等人在文献［17－19］中分别借助非线性耦合分析和相平面法规划了一系列台车轨迹，实现了良好的控制性能.离线规划的轨迹一般用于前馈环节，在复杂的工作环境中，需要与反馈控制器相结合，以提高系统对外界干扰的鲁棒性.

输入整形的核心思想则是利用系统的频率特性以及阻尼比等信息，对控制信号进行合理规划.为此，需要获得一组整形脉冲序列(也称整形器)，并将其与目标控制指令进行卷积，然后得到输入信号来对系统施加控制［20－21］，这种方法在实际欠驱动起重机系统中获得了成功应用.具体而言，S.Garrido等人将输入整形方法成功地应用于一个装配了传感器的大型三维桥式起重机上，实现了负载的精确定位，且在整个传送过程中，负载摆动保持在很小的范围内［22］.在文献［23］中，E.Maleki等分析了臂式起重机中悬臂的旋转及俯仰运动对负载摆动的影响，并将零摆动整形器应用于负载的防摆控制，结果表明该方法可将摆动幅度降低76%.一般情况下，起重机负载的运动可近似看作单摆运动，但在某些特定情况下，一些类型的负载与绳索会表现出双摆效应，导致负载的摆动信息无法测量.为此，美国佐治亚理工学院的W.Singhose等人基于线性化定绳长的双摆吊车模型，设计了一种对系统在一定频率范围均有效的输入整形器，它既有效地抑制了负载摆动，又提高了系统对参数变化的鲁棒性［24］，随后，他们又成功地将该方法引入到具有双摆效应的臂式起重机的负载防摆控制［25］.

2.3 部分反馈线性化方法

对于全驱动系统而言，往往可以为其设计合适的控制器将其完全反馈线性化，从而实现良好的控制性能(如误差指数收敛等).然而，由于欠驱动连杆系统自身的驱动数目不够，因此不能对其进行完全反馈线性化.为此，控制专家M.W.Spong教授针对欠驱动系统提出了一种部分反馈线性化方法，此方法通过定义一个新的控制量来实现系统变换，最终将其进行局部线性化［26－27］，该方法被广泛地应用于欠驱动连杆系统的控制［28－30］.如在文献［29］中，张晓华等人对桥式起重机的欠驱动模型进行了部分反馈线性化，通过坐标变换将其转换为严格前馈级联规范型，并在此基础之上设计了饱和控制器，实现了负载的准确定位.高丙团等则基于非配置部分反馈线性化方法为Furuta pendulum设计了一个状态反馈控制器，将摆杆迅速摇起到不稳定平衡点附近，然后切换到一个线性全状态平衡控制器，实现了系统的稳定控制［30］.值得指出的是，经过部分反馈线性化后得到的系统仍然是非线性的，且其耦合性比变换之前更强，导致控制器结构也变得更为复杂.

2.4 能量(无源)方法

一个系统的能量能反映它的运动状态，俄国数学家李雅普诺夫(Lyapunov)所提出的稳定性直接分析方法，就是受物体运动时能量变化规律的启发而得到的.通过分析系统的能量，可以方便地处理系统的欠驱动非线性特性.因此，基于能量分析的策略自然地成为控制欠驱动连杆系统的有力武器.根据欠驱动连杆系统的动力学模型(1)，可得其能量为

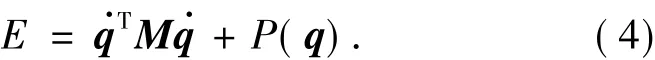
式中:P(q)表示系统势能，满足 G(q)=∂P(q)/∂q，其他变量的定义同式(1).对式(4)关于时间求导数，并结合性质1和2，可得

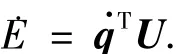
对其两边关于时间求积分，有

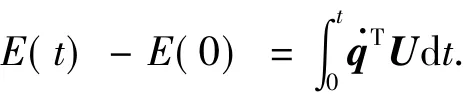
那么，以U(t)为输入，˙q(t)为输出的系统是耗散、无源的.根据这一特性，国内外学者利用基于能量的方法，对欠驱动连杆系统开展了广泛研究［5－9，11－12，31－37］.其中，著名控制专家K.J.Astrom等［32］将能量分析方法应用于单倒立摆系统的摇起控制，得出了小车的加速度与重力加速度应满足的关系，并将其在不同摆长的双倒立摆系统上进行了应用.遗憾的是，他们没有考虑小车在水平方向的运动，也没有给出双倒立摆情形的稳定性分析.为此，X.Xin等人借助不变集的稳定性理论完成了双倒立摆系统的渐近收敛分析［33］.通过对欠驱动机械臂的无源性分析，I.Fantoni和X.Xin等分别构造了包含能量平方项的李雅普诺夫函数，并设计了能量耦合控制律，使得系统状态能进入竖直方向任意小的邻域，为平衡控制器的设计提供了保证［7－8］.除了摇起运动外，能量方法还可用于对系统的平衡控制［5－6］.在文献［5］中，E.Li等充分考虑了球棒系统中棒的长度，针对系统不同的平衡点分别设计了平衡稳定控制器.自2001年起，方勇纯研究组将能量方法广泛地应用于桥式起 重 机 的 控 制［9，11－12，34－37］. 具 体 而 言，文 献［9］和［36］提出了一系列基于能量的非线性控制器以增强台车和负载之间的耦合特性，实验结果证明了该控制策略的有效性.随后，考虑到系统参数的不确定性及外界干扰的影响，他们又设计了自适应控制器来提高能量控制方法对实际工作环境的适应能力［11－12，36－37］.

2.5 变量降维法

由于欠驱动连杆系统中包含了非直接驱动的运动自由度，限制了常规非线性控制策略的应用.为突破这一瓶颈，可以通过定义合适的复合变量来对系统进行降维处理，使新的状态变量个数等于控制输入维数，将系统转换为以新变量为状态的“全驱动系统”，之后就可以进行常规的控制器设计与分析.在此，把基于这种思想的控制方法称为变量降维法，常见的降维处理方法可归为以下2类:

1)将驱动变量和欠驱动变量进行组合生成新的综合变量［38］，并以之为基础来设计控制器.以桥式起重机为例，H.Lee等人将台车位移误差、速度误差和负载摆角通过线性组合得到一个复合变量，并且证明了当该变量趋于零时，各分量渐近收敛，在此基础上设计了常规的滑模控制器使复合变量收敛于零，从而实现了系统镇定［39］.文献［40］则将可驱动量和不可驱动量通过非线性组合得到一个新的变量，然后借助标准的反步法为一类欠驱动系统设计了一种半全局镇定控制器，并将其成功地应用于倒立摆系统.

2)定义分级滑模面，即为可驱动状态和不可驱动状态分别定义一级滑模面，然后将一级滑模面线性组合为二级滑模面，进而可借助滑模控制等方法来设计控制器.由于滑模面的引入，该方法可保证控制系统对外界干扰与模型不确定性的鲁棒性.在文献［41］中，中科院自动化所的易建强教授研究组针对一类欠驱动系统，采用分级滑模方法，定义了分级滑模面，并证明了各级滑模面的稳定性，从而保证了所有系统状态的渐近收敛.之后，他们又将该方法用于倒立摆与Pendubot的控制，都取得了较好的效果［42－43］.针对水平欠驱动机械臂的控制问题，林壮等人为系统变量定义了分级滑模面，并设计了自适应反向递推控制律，避免了常规滑模控制器的抖振(chattering)现象，实现了整个系统的渐近镇定［44］.

2.6 分级控制设计法

与变量降维法相类似，另一种常见的控制方法是先为驱动状态和不可驱动状态分别设计虚拟控制量，使得它们能达到各自的期望状态，然后将这些虚拟控制量通过组合生成新的控制量，并将其作为系统最终的控制输入.本文称这种设计策略为分级控制设计法，该方法可提高控制系统设计的灵活性.具体而言，针对桥式起重机的控制问题，孙宁等首先为台车的水平运动选取了一条参考轨迹以保证台车的精确定位，同时为负载设计了抗摆环节来抑制负载摆动，最后将两者结合在一起，并借助迭代策略对合成轨迹进行修正，实现了良好的控制性能［17－18］.文献［45］则为台车的快速运行和负载的摆角抑制分别设计了模糊位置和防摆控制器，随后将两者线性叠加在一起，作为总的控制输入.一般而言，该方法能较好地实现欠驱动连杆系统的有效控制，然而，在分级设计虚拟控制量后，需将两者通过各种方式进行结合以生成实际控制输入，这样使得最终的实际控制效果为分级设计时期望效果的折衷.为此，在文献［46］中，刘殿通等借助模糊规则，根据当前系统输出的情况来在线调整各个虚拟控制分量之间线性组合的权重，改善了控制性能的“折衷”问题.

2.7 智能控制方法

上述绝大多数方法的控制性能在很大程度上都取决于系统建模的准确度，而智能控制算法，如模糊控制、神经网络和遗传算法等则可以不依赖于模型，并且随着人工智能、模式识别及计算机科学技术的迅速发展，它们开始大量地被应用于欠驱动系统的控制.

模糊控制可以在一定程度上模拟人类的操作经验.针对欠驱动连杆系统，研究人员通常直接将系统的输出或状态量作为模糊输入量来制定相应的模糊规则［47－48］，也有专家将系统一些观测值或辅助变量作为模糊规则的输入，如台湾中原大学的C.Chang等在文献［49］中通过选取台车定位误差与负载位置的投影来计算桥式起重机的控制输入.文献［50］则为机械臂关节定义了能量变量，并根据其制订了相应的模糊规则.一般而言，当参数发生变化时，需要花费大量时间对已有的模糊规则进行调整，这无疑降低了模糊控制的实用性.为此，C.Chang等人设计了一种自适应模糊控制器，它可以根据环境状态在线地调整系统状态的模糊集合，增强系统对各种干扰的鲁棒性［51］.除了直接用于控制器外，模糊方法还可以被用来对欠驱动系统进行建模，然后施加控制.如文献［52］就为桥式起重机建立了T－S模糊系统模型，然后借助线性矩阵不等式方法设计了鲁棒控制器.值得指出的是，尽管模糊控制方法对于欠驱动连杆系统能取得良好的控制效果，但其稳定性通常难以进行严格的数学证明，由于缺乏理论保障，其性能尚有待进行更为深入的研究.

遗传算法和神经网络在欠驱动连杆系统中也有着广泛的应用.遗传算法具有全局最优搜索的能力，被广泛地用于控制算法的优化.在文献［53］中，D.Liu等针对一类欠驱动机械系统设计了一种基于实数型基因演算法的镇定控制器，并将其应用于带有双摆效应的桥式起重机系统.神经网络控制器可在系统模型未知的情况下对系统进行有效控制［54］，但在应用时需要通过大量的训练来辨识内部权值.鉴于遗传算法的优化能力，很多专家将其应用于欠驱动连杆系统的控制，提出了基于遗传算法的神经网络控制器［55－56］.其中，对于臂式起重机的防摆控制，日本学者K.Nakazono等构造了一个3层神经网络控制器，并借助实值编码遗传算法对其进行训练［56］.当应用于欠驱动连杆系统时，神经网络除了直接用于控制器之外，还在建模、软测量等方面有着更广泛的应用.R.Toxiqui等［57］通过径向基神经网络补偿起重机系统的不确定性，减小了闭环系统的静态误差;文献［58］则借助神经网络构造一个软传感器(soft sensor)，根据电流变化来估计系统的状态值，代替传统起重机中测量台车位置和负载摆角的传感器，极大地降低了系统成本.

3 结论与展望

欠驱动系统的控制是非线性控制理论中最具挑战性的方向之一.纵观国内外研究现状可知，针对欠驱动(连杆)系统的研究已经取得了长足的进步和丰硕的成果，极大地促进了非线性系统理论的发展.尽管如此，现有的工作仍然处于起始阶段，大部分研究尚停留在理论水平，这给其实际应用带来了很大的困难.很多方法仅适用于解决特定问题的一个方面，且大多基于系统模型完全已知与控制器理想的情况，或者仅考虑实验室环境、系统状态完全可测的情况，一旦系统建模不准确、驱动器饱和、存在外界干扰(包括风力、摩擦、噪声等)、系统状态的检测存在滞后、仅有部分系统状态(如输出)可测时，它们往往难以获得令人满意的控制性能，严重时甚至导致系统闭环不稳定.此外，现有的大部分方法仅能保证系统状态的渐近收敛，但从工程应用角度出发，研究人员更希望它们能在有限时间内或以指数方式趋于期望值.

为推进欠驱动系统的理论研究，并将其与实际应用相结合，笔者认为在以下几个方面有待进一步展开研究.

1)系统模型不确定性与外界干扰补偿.在系统建模时，通常会忽略高阶项，导致模型与系统的实际特性之间存在较大差异.此外，系统参数总是存在测量误差，有的甚至很难直接测量，而许多控制方法对参数变化非常敏感，建模误差会显著降低系统的控制性能.除建模误差外，现有的研究结果大多没有充分考虑各种外界干扰的影响，往往是对其进行粗略补偿，或忽略不计.而在实际应用中，这些因素对控制性能影响很大.为此，笔者认为对于这些外界干扰，可通过自适应、滑模等非线性策略对其进行反馈补偿，亦可借助神经网路或其他智能方法进行前馈抑制.

2)执行器饱和情况下的控制策略.如文中所述，大多数控制策略都假设控制器是完全理想的.然而，实际物理系统的驱动能力是有限的，一旦执行器饱和，会严重影响控制算法的有效性，严重时甚至导致系统崩溃.因此，在有限能力范围内如何实现欠驱动连杆系统的有效控制具有非常重要的工程应用价值.为了解决上述问题，可以从以下2个方面着手来提高控制方法的实用性:一方面，可以进一步研究饱和控制方法和理论，解决常规饱和策略依赖于系统参数的问题;另一方面，可将执行器极限作为性能指标或者约束引入到控制器设计过程，并借助现有的非线性理论进行稳定性分析.

3)有限时间控制研究.要对连杆系统的欠驱动状态实施控制，必须借助它们与可驱动状态之间的动态耦合关系间接进行.现有结果往往仅能保证不可驱动状态渐近趋于期望值，而事实上，系统状态在有限时间内收敛更具实际意义.为此，需要对欠驱动系统的有限时间控制策略展开深入研究.例如终端滑模控制方法通过构造非线性终端滑模面可保证系统状态在有限时间内收敛，且对参数摄动和外界干扰具有强鲁棒性，非常具有研究价值.

4)输出反馈控制策略.对于实际系统而言，考虑到传感器成本以及系统结构复杂度等问题，往往仅能对系统的输出(如位移、角度等)进行检测，而其他的系统状态(如速度、角速度等)一般不能直接获取.此外，由于输出信号往往存在噪声，直接对其进行差分等运算将不能准确地获取速度信号.目前，针对欠驱动系统的控制策略多数基于全状态反馈，限制了其在实际工程系统中的应用.为此，需要对欠驱动系统的输出反馈控制进行深入的研究，可以通过设计观测器等方法，充分利用可测的输出信号，来对不可测的系统状态进行在线估计，从而提高控制策略的实用性.

5)系统状态检测的滞后问题.在实际工程中，许多欠驱动系统的输出量检测与其变化量之间存在延迟，如对于工作在建筑工地中的塔式起重机系统而言，其吊绳长度一般较长，呈现出显著的柔性特征，使得负载的摆动(位于吊绳末端)与传感器(位于吊绳始端)测量信号之间存在明显的滞后问题.如不能在控制器设计与分析时充分考虑反馈信号的滞后性，将极有可能导致控制任务的失败.为此，笔者认为可以借助智能预测控制等策略，充分利用已获取的摆角信号，对负载的实时摆动进行合理预测，用于补偿滞后问题，进而提高控制系统的实际性能.

6)非惯性系中的控制策略.目前，几乎所有与欠驱动连杆系统相关的文献都专注于系统在惯性系(地球)中的运动情况与控制策略，而很少有人考虑非惯性系统中欠驱动连杆系统的研究.事实上，随着航天科技与无人技术的迅速发展，空间机器人必将得到广泛的应用，而在复杂的太空势场下(如超重、失重等)，惯性系中的控制策略很难直接被推广.因此，非常有必要在今后的研究中考虑并模拟非惯性系势场带来的影响，为实现欠驱动连杆系统的完全自动化迈出重要的一步.

［1］KOLMANOVSKY I，MCCLAMROCH N.Developments in nonholonomic control problems［J］.IEEE Control Systems Magazine，1995，15(6):20－36.

［2］ABDEL－RAHMAN E，NAYFEH A，MASOUD Z.Dynamics and control of cranes:a review［J］.Journal of Vibration and Control，2003，9(7):863－908.

［3］FANTONI I，LOZANO R.Global stabilization of the cartpendulum system using saturation functions［C］//Proceedings of the IEEE Conference on Decision and Control.Maui，USA，2003:4393－4398.

［4］FREIDOVICH L，SHIRIAEV A，GORDILLO F，et al.Partial－energy－shaping control for orbital stabilization of highfrequency oscillations of the Furuta pendulum［J］.IEEE Transactions on Control Systems Technology，2009，17(4):853－858.

［5］LI En，LIANG Zize，HOU Zengguang，et al.Energy－based balance control approach to the ball and beam system［J］.International Journal of Control，2009，82(6):981－992.

［6］高丙团.TORA的动力学建模及基于能量的控制设计［J］.自动化学报，2008，34(9):1221－1224.

GAO Bingtuan.Dynamical modeling and energy－based control design for TORA［J］.Acta Automatica Sinica，2008，34(9):1221－1224.

［7］XIN X，KANEDA M.New analytical results of the energy based swinging up control of the Acrobot［C］//Proceedings of the IEEE Conference on Decision and Control.Atlantis，Bahamas，2004:704－709.

［8］FANTONI I，LOZANO R，SPONG M.Energy based control of the Pendubot［J］.IEEE Transactions on Automatic Control，2000，45(4):725－729.

［9］FANG Y，DIXON W，DAWSON D，et al.Nonlinear coupling control laws for an underactuated overhead crane system［J］.IEEE/ASME Transactions on Mechatronics，2003，8(3):418－423.

［10］LI W，TANAKA K，WANG H.Acrobatic control of a Pendubot［J］.IEEE Transactions on Fuzzy Systems，2004，12(4):549－552.

［11］MA Bojun，FANG Yongchun，ZHANG Xuebo.Adaptive tracking control for an overhead crane system［C］//Proceedings of the IFAC World Congress.Seoul，Korea，2008:12194－12199.

［12］FANG Yongchun，MA Bojun，WANG Pengcheng，et al.A motion planning based adaptive control method for an underactuated crane system［J］.IEEE Transactions on Control Systems Technology(accepted).

［13］SAKAWA Y，SHINDO Y.Optimal control of container cranes［J］.Automatica，1982，18(3):257－266.

［14］AUERNIG J，TROGER H.Time optimal control of over－head cranes with hoisting of the load［J］.Automatica，1987，23(4):437－447.

［15］TERASHIMA K，SHEN Y，YANO K.Modeling and optimal control of a rotary crane using the straight transfer transformation method［J］.Control Engineering Practice，2007，15(9):1179－1192.

［16］XU Y，IWASE M，FURUTA K.Time optimal swing－up control of single pendulum［J］.ASME Journal of Dynamic Systems，Measurement，and Control，2001，123(3):518－527.

［17］SUN Ning，FANG Yongchun，MA Bojun.Motion planning for overhead cranes based on iterative strategy［C］//Proceedings of the Chinese Control Conference.Beijing，China，2010:326－331.

［18］SUN Ning，FANG Yongchun，ZHANG Yudong，et al.A novel kinematic coupling－based trajectory planning method for overhead cranes［J］.IEEE/ASME Transactions on Mechatronics(accepted).

［19］SUN Ning，FANG Yongchun，ZHANG Xuebo，et al.Phase plane analysis based motion planning for underactuated overhead cranes［C］//Proceedings of the 2011 International Conference on Robotics and Automation.Shanghai，China，2011:3483－3488.

［20］KHALID A，HUEY J，SINGHOSE W，et al.Human operator performance testing using an input－shaped bridge crane［J］.Journal of Dynamic Systems，Measurement，and Control，2006，128(4):835－841.

［21］SORENSEN K，SINGHOSE W，DICKERSON S.A controller enabling precise positioning and sway reduction in bridge and gantry cranes［J］.Control Engineering Practice，2007，15(7):825－837.

［22］GARRIDO S，ABDERRAHIM M，GIMENEZ A，et al.Anti－swinging input shaping control of an automatic construction crane［J］.IEEE Transactions on Automation Science and Engineering，2008，5(3):549－557.

［23］MALEKI E，SINGHOSE W.Dynamics and zero vibration input shaping control of a small－scale boom crane［C］//Proceedings of the American Control Conference.Baltimore，USA，2010:2296－2301.

［24］SINGHOSE W，KIM D，KENISON M.Input shaping control of double－pendulum bridge crane oscillations［J］.Journal of Dynamic Systems，Measurement，and Control，2008，130(3):1－7.

［25］MALEKI E，SINGHOSE W，SRINIVASAN S.Positioning and control of boom crane luffing with double－pendulum payloads［C］//Proceedings of the IEEE International Conference on Control Applications:Part of IEEE Multi－Conference on Systems and Control.Yokohama，Japan，2010:1319－1324.

［26］SPONG M.Partial feedback linearization of underactuated mechanical systems［C］//Proceedings of the IEEE/RSJ/GI International Conference on Intelligent Robots and Systems.Munich，Germany，1994:314－321.

［27］SPONG M，PRALY L.Control of underactuated mechanical systems using switching and saturation［C］//Proceedings of Block Island Workshop Control Using Login Based Switching.Block Island，USA，1995:162－172.

［28］BURG T，DAWSON D，RAHN C.Nonlinear control of an overhead crane via the saturating control approach of Teel［C］//Proceedings of the IEEE International Conference on Robotics and Automation.Minneapolis， USA， 1996:3155－3160.

［29］张晓华，郭源博.基于嵌套饱和方法的吊车系统非线性控制［J］.控制工程，2008，15(2):113－115，212.

ZHANG Xiaohua，GUO Yuanbo.Nonlinear control of overhead crane based on nested saturation approach［J］.Control Engineering of China，2008，15(2):113－115，212.

［30］高丙团，张晓华，陈宏钧.基于快速起摆的Furuta摆切换控制系统［J］.控制与决策，2008，23(11):1277－1280，1285.

GAO Bingtuan，ZHANG Xiaohua，CHEN Hongjun.Switching control of Furuta pendulum system with aggressive swing－up［J］.Control and Decision，2008，23(11):1277－1280，1285.

［31］HU G，MAKKAR G，DIXON W.Energy－based nonlinear control of underactuated Euler－Lagrange systems subject to impacts［J］.IEEE Transactions on Automatic Control，2007，52(9):1742－1748.

［32］ASTROM K，FURUTA K.Swinging up a pendulum by energy control［J］.Automatica，2000，36(2):287－295.

［33］XIN X，KANEDA M.Analysis of the energy－based control for swinging up two pendulums［J］.IEEE Transactions on Automatic Control，2005，50(5):679－684.

［34］FANG Y，ZERGEROGLU E，DIXON W，et al.Nonlinear coupling control laws for an overhead crane system［C］//Proceedings of the IEEE International Conference on Control Applications.Mexico City，Mexico，2001:639－644.

［35］MA B，FANG Y，ZHANG Y.Switching－based emergency braking control for an overhead crane system［J］.IET Control Theory and Applications，2010，4(9):1739－1747.

［36］马博军，方勇纯，王宇韬，等.欠驱动桥式吊车系统自适应控制［J］.控制理论与应用，2008，25(6):1105－1109.

MA Bojun，FANG Yongchun，WANG Yutao，et al.Adaptive control for an underactuated overhead crane system［J］.Control Theory ＆ Applications，2008，25(6):1105－1109.

［37］孙宁，方勇纯，王鹏程，等.欠驱动三维桥式吊车系统自适应跟踪控制器设计［J］.自动化学报，2010，36(9):1287－1294.

SUN Ning，FANG Yongchun，WANG Pengcheng，et al.Adaptive trajectory tracking control of underactuated 3－dimensional overhead crane systems［J］.Acta Automatica Sinica，2010，36(9):1287－1294.

［38］MARTON L，LANTOS B.Stable adaptive ball and beam system［C］//Proceedings of the IEEE International Confer－ence on Mechatronics.Budapest，Hungary，2006:507－512.

［39］LEE H，LIANG Y，SEGURA D.A sliding－mode antiswing trajectory control for overhead cranes with high－speed load hoisting［J］.Journal of Dynamic Systems，Measurement，and Control，2006，128(4):842－845.

［40］PARK M，CHWA D，HONG S.Semi－global stabilization of a class of underactuated Euler－Lagrange systems by backstepping approach［C］//Proceedings of the SICEICASE International Joint Conference.Bexco， Korea，2006:811－815.

［41］WANG W，YI J，ZHAO D，et al.Design of a stable sliding—mode controller for a class of second－order underactuated systems［J］.IEE Proceedings—Control Theory and Applications，2004，151(6):683－690.

［42］QIAN Dianwei，YI Jianqiang，ZHAO Dongbin.Robust control using sliding mode for a class of under－actuated systems with mismatched uncertainties［C］//Proceedings of the IEEE International Conference on Robotics and Automation.Roma，Italy，2007:1449－1454.

［43］QIAN Dianwei，YI Jianqiang，ZHAO Dongbin.Hierarchical sliding mode control to swing up a Pendubot［C］//Proceedings of the American Control Conference.New York，USA，2007:5254－5259.

［44］林壮，段广仁，宋申民.水平欠驱动机械臂的反步自适应滑模控制［J］.机器人，2009，31(2):131－145.

LIN Zhuang，DUAN Guangren，SONG Shenmin.Backstepping adaptive sliding mode control for horizontal underactuated manipulators［J］.Robot，2009，31(2):131－145.

［45］王晓军，邵惠鹤.基于模糊的桥式起重机的定位和防摆控制研究［J］.系统仿真学报，2005，17(4):936－939.

WANG Xiaojun，SHAO Huihe.Fuzzy logic－based antiswing and position control for bridge cranes［J］.Journal of System Simulation，2005，17(4):936－939.

［46］LIU Diantong，YI Jianqiang，ZHAO Dongbin，et al.A－daptive sliding mode fuzzy control for a two－dimensional overhead crane［J］.Mechatronics，2005，15(5):505－522.

［47］ZHANG Jinming，LI Renhou，ZHANG Ping’an.Stability analysis and systematic design of fuzzy control systems［J］.Fuzzy Sets and Systems，2001，120(1):65－72.

［48］LIU Qingbo，YU Yueqing，XIA Qixiao，et al.A new fuzzy method for the motion control of underactuated robots based on genetic algorithm［C］//Proceedings of the International Conference on Fuzzy Systems.Hong Kong，China，2008:999－1003.

［49］CHANG C，CHIANG K.Fuzzy projection control law and its application to the overhead crane［J］.Mechatronics，2008，18(10):607－615.

［50］ICHIDA K，WATANABE K，IZUMI K，et al.Fuzzy switching control of underactuated manipulators with approximated switching regions［C］//Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems.Beijing，China，2006:586－591.

［51］CHANG Chengyuan.Adaptive fuzzy controller of the overhead cranes with nonlinear disturbance［J］.IEEE Transactions on Industrial Informatics，2007，3(2):164－172.

［52］周灌中，罗枚.基于T－S模型的集装箱桥吊防摆H∞控制［J］.控制理论与应用，2008，25(2):268－272.

ZHOU Guanzhong，LUO Mei.Takagi－Sugeno model－based H－infinity anti－swing control for container crane［J］.Control Theory ＆ Applications，2008，25(2):268－272.

［53］LIU Diantong，GUO Weiping，YI Jianqiang.Dynamics and GA－based stable control for a class of underactuated mechanical systems［J］.International Journal of Control，Automation，and Systems，2008，6(1):35－43.

［54］JUNG S，KIM S.Control experiment of a wheel－driven mobile inverted pendulum using neural network［J］.IEEE Transactions on Control Systems Technology，2008，16(2):297－303.

［55］王清，马广富，弥曼.一种基于遗传算法的神经网络控制方法研究［J］.系统仿真学报，2006，18(4):1070－1077.

WANG Qing，MA Guangfu，MI Man.Research on neural network control based on genetic algorithm［J］.Journal of System Simulation，2006，18(4):1070－1077.

［56］NAKAZONO K，OHNISHI K，KINJO H，et al.Vibration control of load for rotary crane system using neural network with GA－based training［J］.Artificial Life and Robotics，2008，13(1):98－101.

［57］TOXQUI R，YU W，LI X.PD control of overhead crane systems with neural compensation［C］//Proceedings of the International Joint Conference on Neural Networks.Vancouver，Canada，2006:4697－4703.

［58］SOLIHIN M，WAHYUDI，ALBAGUL A.Development of

soft sensor for sensorless automatic gantry crane using RBF neural networks［C］//Proceedings of the IEEE Conference on Cybernetics and Intelligent Systems.Bangkok，Thailand，2006:1－6.

孙宁，男，1988年生，博士研究生，主要研究方向为欠驱动系统的自适应控制、学习控制、滑模控制以及模糊控制等.

方勇纯，男，1973年生，教授，博士生导师，IEEE高级会员，中国人工智能学会理事，中国自动化学会控制理论专业委员会委员、智能自动化专业委员会委员.主要研究方向为复杂系统非线性控制、机器人视觉控制等.2006年入选教育部“新世纪优秀人才支持计划”，2009年获得“天津市优秀留学人员”称号，2010年获得第10届天津青年科技奖.发表学术论文近百篇，其中被SCI、EI检索80篇.

A review for the control of a class of underactuated systems

SUN Ning，FANG Yongchun
(Institute of Robotics and Automatic Information System，Nankai University，Tianjin 300071，China)

Recently，research on underactuated systems has become a hot topic in the robotics and automation fields.The research status for the control of a class of underactuated systems(termed as underactuated link systems)was reviewed in this paper.Specifically，the system dynamics was presented first，and two basic control modes were introduced.Subsequently，the main control strategies，which include optimal control methods，motion planning methods，partial feedback linearization methods，energy－based methods，state dimension reducing methods，hierarchical control design methods，and intelligent schemes，were analyzed.Finally，some major issues associated with the control system design for underactuated link systems，such as robustness，practicability，rapidness and so on，were sketched，and corresponding prospects including robust strategy，saturation control and finite time control etc.were proposed for future work.

underactuated systems;robotics;intelligent control

TP273

A

1673－4785(2011)03－0200－08

10.3969/j.issn.1673－4785.2011.03.002

2011－03－31.

国家自然科学基金资助项目(60875055);天津市应用基础及前沿技术研究计划重点项目(08JCZDJC21800).

方勇纯.E－mail:yfang@robot.nankai.edu.cn.