地铁盾构结构设计方法探讨

彭钧

（北京交通大学土木建筑学院，北京100044）

当前，北京、上海、广州等城市的地铁隧道建设正处在高峰阶段。采取盾构工法来修筑地铁，因其快速安全的特点已经得到了非常广泛的应用。而管片作为盾构工法中非常重要的衬砌手段，其设计和制造费用占整个盾构隧道建设的很大比重。因此探讨分析管片的设计合理性，提高工程经济性，显得尤为必要。

1 管片截面内力计算理论

以我国的地下结构设计实践来看，盾构隧道的计算方法有很多种，通常使用的有3类[1]：修正惯用法、多铰圆环法和梁-弹簧法。由于多铰圆环法对于接头的处理是将其简化为铰结构，这就要求在盾构管片拼装完毕后将接头拆除或者采用特殊的管片接头形式。所以，此种方法适合于围岩较为稳定的国家和地区使用，而不适合于我国目前的地质现状[2-3]。故文中主要讨论修正惯用法和梁-弹簧法对管片模型的影响。

1.1 修正惯用法理论

修正惯用法[4]的主要思路是将管片整环视为刚度均匀的环，同时为了考虑管片接头处的弯曲刚度降低而引入了一个折减系数η（η＜1.0）。通过这个系数来降低管片环整体的抗弯刚度，以处理接头处的情况。进一步考虑管片的错缝拼接效应，再引入一个系数ζ（ζ＜1.0）。并以（1+ζ）作为管片体弯矩的增大系数，（1-ζ）作为管片接头弯矩的减小系数，以此评价管片环的 弯矩不均匀分配，通常 0.6≤η≤0.8，0.3≤ζ≤0.5。修正惯用法的受力情况如图1示，截面内力情况如图2示，错缝拼装效应的弯矩分配如图3示。该法的荷载确定和内力计算公式可参见文献[5-6]。

图1中，Pw1表示垂直方向上的水压，Pe1表示垂直方向上的土压，P0表示上覆荷载，Hv表示隧道顶部到水平面的距离，H表示隧道顶部到地表面的距离，Pe2表示水平方向上的土压，Pw2表示水平方向上的水压，Pg表示自重反力，R0表示外缘半径，R1表示内缘半径，Rc表示轴线半径，g表示衬砌自重。图2中Q表示剪力，M表示弯矩，N表示轴力。图3中B表示衬砌宽度。

图1 管片所受外荷载示意图Fig.1 External load of segment

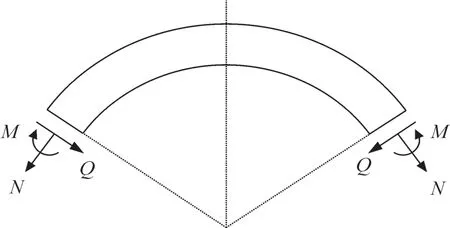
图2 管片截面内力示意图Fig.2 Internal force of segment

图3 管片弯矩分配示意图Fig.3 Bending moment distribution of segment

1.2 梁-弹簧法理论

梁-弹簧模型通常是通过直梁-弹簧或者曲梁-弹簧单元来模拟的，如图4所示。朱合华等[7]证明了当部分单元取的足够精细时，直梁-弹簧模型是可以取代曲梁-弹簧模型的，因此后文在计算时采用的是直梁-弹簧模型。对于此种模型，还采用了旋转弹簧来模拟管片环向接头，剪切弹簧来模拟管片环与环之间的接头，用径向和切向地层弹簧来模拟地层与管片环之间的相互作用[8]，此种模型能较好的反映管片在地层中的受力情况。图4中，K1为剪切刚度，K2为轴向刚度，Kθ为转动刚度。

图4 梁-弹簧计算单元模型Fig.4 Model of beam-spring calculating unit

2 管片裂缝合理性建议及工程实例应用比较

2.1 管片裂缝控制合理性建议

管片的裂缝控制是管片设计中的重要一环，不仅仅是关于受力安全和耐久性的考虑，还有经济效益的影响。配筋也要在保证受力安全的同时，注意裂缝的情况。从综合的角度来看，单纯的提高配筋率并不是一个好的方法。需要结合多种合理化的配置方法来实现，以下提出一些结合理论研究及工程实例的管片配置的合理性建议：

1）盾构在隧道推进的过程中，应适当的加注泡沫剂，以减小掘进时的扭矩和推力，如文献[9]中所述，发泡液浓度为2%～3%的泡沫应用于土压平衡盾构较为理想。并合理的控制盾构掘进速度，盾构的推进推力可按照文献[9]中给出的设计推力公式2.1来计算，既规避了围岩风险，又减小因盾构机在曲线掘进时管片产生裂缝的可能。

式中：Fd为设计推力，kN；F1为盾构外壳与周围地层的摩阻力，kN；F2为盾构机推进时的正面推进阻力，kN；F3为管片与盾尾间的摩阻力，kN；F4为盾构机切口环贯入地层时的阻力，kN；F5为变向阻力，kN；F6为后接台车的牵引阻力，kN。

2）根据不同的地质类型，研究各种情况下的管片受力机理，通过合理的计算模型选择，使得配筋和管片尺寸配置更加合理。

3）合理分析经济效益和衬砌安全的平衡点，避免不合理的加大管片钢筋，和前期节约资金造成后期处理费用加大的情况。建议在管片局部改善配筋方式使其受力性能改善，增加螺栓孔、手孔处抵抗开裂的能力。同时，此处阐述一种设计思路，在普通钢筋混凝土的管片基础上提出设计低配筋率钢纤维钢筋混凝土。根据文献[10]中的实验结论，可以看出，低配筋率钢纤维钢筋混凝土初始裂缝荷载240 kN大于普通钢筋混凝土的220 kN，且产生0.2 mm裂缝宽度下的荷载为440 kN，比普通钢筋混凝土的400 kN高出了约10%的性能。可见工程应用上是有利的，但是在工程中如何实现制作此类管片，则仍然有待解决。

2.2 工程实例应用比较

1）工程概况。该工程系北京某地铁盾构隧道，所处第四系地层。土层自上而下分别为：人工填土、粉土、粉砂细砂、粉质黏土、砂土、卵石、园砾等等。其中隧道结构覆土为填土、粉细砂、粉土、粉质粘土。覆土厚度为10.8～18.8 m，地下水位一般在23 m左右。地质土层相关参数见表1，管片衬砌相关参数见表2。

表1 地质土层相关参数Tab.1 Related parameters of geological soil

表2 管片衬砌相关参数Tab.2 Related parameters of segment lining

2）修正惯用法计算结果。通过计算软件采用修正惯用法，根据相关文献[3，12-14]代入相关的参数，此处取值，η=0.8，ζ=0.3。由此计算得出隧道管片衬砌环的内力图，如图5，图6所示。而从图中可得出该管片环的最不利内力组合：1处最大正弯矩：M=146.23 kN·m，N=438.33 kN；2处最大负弯矩：M=-118.78 kN·m以及N=661.15 kN。

图5 管片轴力示意图（单位kN）Fig.5 Axial force of segment

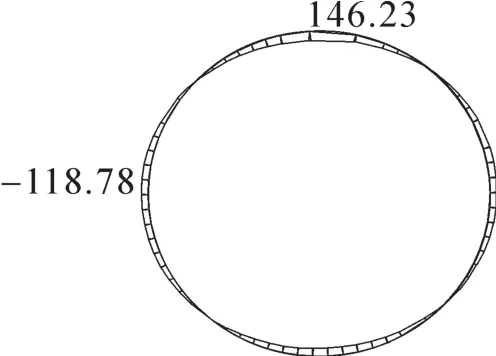
图6 管片弯矩示意图（单位kN·m）Fig.6 Bending moment distribution of segments

3)梁-弹簧法计算结果。运用计算软件，并结合实际资料和经验修改默认刚度值，此处径向弹簧抗剪刚度取值为Kr=1×106kN·m-1，切向弹簧抗剪刚度为Kt=1×106kN·m-1，环向弹簧转动刚度为Kθ=5.0×104kN·rad-1，Kθ=3.0×104kN·rad-1，以此计算管片衬砌环内力。计算理论如前文所述，同理，此时的管片环最不利内力组合：最大正弯矩：M=152.52 kN·m，N=398.77 kN；最大负弯矩：M=-135.02kN·m，N=760.33 kN。

4）结果对比分析。经表3数据，比较可知，修正惯用法并没有考虑到弯矩的接头作用，计算时偏于安全考虑，且弯矩图较为对称。梁－弹簧法则是考虑了接头作用，比如接头位置是并不是对称的，而非修正惯用法中仅仅在整体管片环的弯矩上乘以一个系数，所以由于接头位置不同，且接头位置分布的不均匀，梁-弹簧法所得出的弯矩是不对称的，弯矩值较修正惯用法小。此外，对于两种模型的精确性的比较，梁-弹簧和修正惯用法虽然荷载模型都是一致的，但是在计算中对于各个接头的位置以及所模拟成的弹簧，在梁-弹簧法中都给予了考虑，故梁-弹簧法包含的因素更多更全面，而不是像修正惯用法一样，简单的乘以一个系数笼统的将整环管片视为同种刚度的模型，所以梁-弹簧法的计算更加接近工程情况。另外，根据文献[11]中的论述，根据弯矩和轴力的不同而减少的配筋量，大致估算梁-弹簧法可每环节省钢筋用量约110 kg。使得盾构隧道的配置更加合理经济。

表3 计算结果比较Tab.3 The comparison of the calculated resuts

3 结语

根据盾构隧道工程实例可以看出修正惯用法和梁-弹簧法都适用于盾构隧道的管片设计。但是修正惯用法趋于保守，采用梁-弹簧法则可以更加贴近实际工程情况，并优化减少配筋的使用量。因此建议在盾构管片设计时，可以优先考虑梁-弹簧法设计，并用修正惯用法予以校核。从而使整个工程趋于合理化，

经济化。

[1]刘建航，候学渊.盾构法隧道[M].北京：中国建筑工业出版社，1997.

[2]朱伟，胡如军，钟小春.几种盾构隧道管片设计方法的比较[J].地下空间，2003，23（4）：352-355.

[3]张厚美，吕国梁.圆形隧道衬砌结构计算模型综述[J].世界隧道，2000，6（2）：1-5.

[4]陈中，喻渝.修正惯用设计法在盾构管片结构计算中的应用和体会[J].科学技术通讯，2002（4）：17-19.

[5]张凤祥，朱合华.傅德明.盾构隧道[M].北京：人民交通出版社，2004.

[6]日本土木学会.隧道标准规范（盾构篇）及解说[M].朱伟，译.北京：中国建筑工业出版社，2001.

[7]朱合华，陶履彬.盾构隧道衬砌结构受力分析的梁一弹簧系统模型[J].岩土力学，1998，19（2）：26-32.

[8]朱合华，崔茂玉，杨金松.盾构衬砌管片的设计模型与荷载分布的研究[J].岩土工程学报，2000，22（2）：190-194.

[9]张凤祥，朱合华，傅德明.盾构隧道[M].北京：人民交通出版社，2004.

[10]闫鑫，龚秋明，姜厚停.土压平衡盾构施工中泡沫改良砂土的试验研究[J].地下空间与工程学报，2010，6（3）：450-453.

[11]郭玉海，陈丹，袁大军.北京地铁盾构隧道管片设计合理性探讨[J].北京：市政技术，2006，24（4）：244-247.

[12]GB 50010-2002.混凝土结构设计规范[S].

[13]GB 50157-2003.地铁设计规范[S].

[14]GB 50009-2001.建筑结构荷载规范[S].