埃特金加速迭代法在水力计算中的应用

乔双全

(齐齐哈尔市水利勘测设计研究院，黑龙江齐齐哈尔161006)

0 引言

水力学公式多是包含多个参数的隐式非线性方程，通常需要试算。迭代法是常用而有效的方法，常用的迭代法有直接迭代法、二分法、截弦法、牛顿法等。由于水力学方程大多非线性化程度比较高，有时候这些迭代法收敛速度慢，同时还有可能迭代发散而导致死循环，从而不能奏效。鉴于这种情况，作者从实际工程应用出发，引入一种新型的迭代计算法——埃特金(Aitken)加速迭代法。埃特金(Aitken)加速法是数值分析中常用的一种迭代收敛的加速算法，可以在保证迭代精度的同时，加快收敛速度。

1 埃特金加速迭代法原理

1.1 不动点迭代法

埃特金加速迭代法属不动点迭代法的一种，首先介绍一下不动点迭代法的原理。

不动点迭代法是一种逐次逼近法，其基本思想是将隐式方程归结为一组显式的计算公式，就是说，迭代过程实质上是一个逐步显示化的过程。

不动点迭代法是将非线性方程f(x)=0，改写成等价显性形式。

选择一个初始值x0，带入(1)式，即可求得x1=φ(x0)如此反复迭代计算

Xk+1=φ(xk)(k=0，1，…) ，φ(x)称为迭代函数。若是方程的一个近似值。

1.2 埃特金加速迭代法

埃特金加速迭代法是不动点迭代法的一种加速收敛算法，用迭代公式校正1次，再校正后采用(4)式改进。

校正

再校正

改进

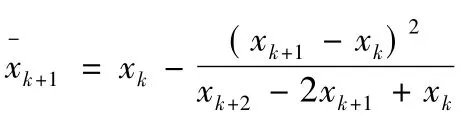
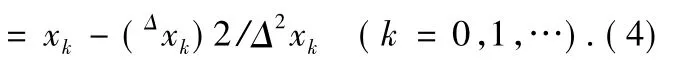
(4)式称为埃特金(Aitken)Δ2加速迭代方法。

2 应用实例

2.1 收缩水深hc计算

收缩水深hc是水力计算中经常试算的一个要素，计算公式形式见公式(5)，其公式是一个隐式的非线性方程，为了试算将其转化为x=g(x)的显式形式，见公式(6)。

式中:T0为总势能，m;q为单宽流量，m2/s;hc为收缩水深，m;α为水流动能校正系数，1.0;φ为流速系数，0.95;g为重力加速度，9.81 m/s2。

例:T0=8.609 m，q=9.333 m2/s，试算侧收缩水深 hc。

首先假设初值 hc0=1.0，带入(6)式校正，得 hc1=0.82919，将 hc1带入(6)再校正得，hc2=0.79852，采用埃特金加速迭代公式对hc1进行修正，再将作为初值进行第二次迭代，至误差满足要求。

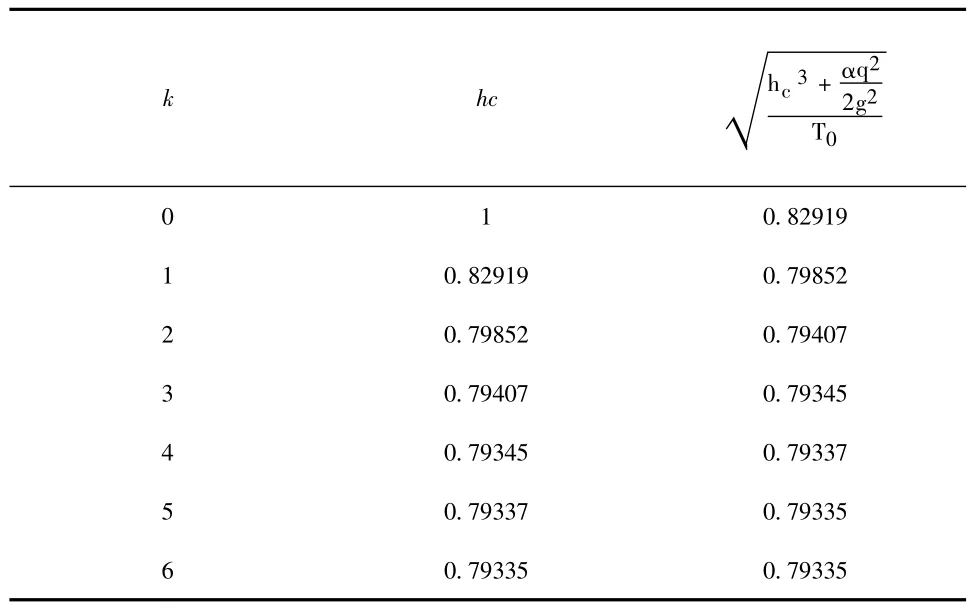
表1 直接迭代法求解hc

表2 埃特金迭代加速法求解hc

由表1、表2计算结果，迭代误差 Δ=1.0×10－5，表1为直接迭代求解法试算过程，表2埃特金加速迭代法试算过程。在相同的迭代误差情况下，埃特金加速迭代法可加速收敛进程。

2.2 梯形渠道临界水深hk计算

临界水深应满足临界方程式:

式中，g为重力加速度，9.81 m/s2，α为动能修整系数，1.0;Ak为相应于hk的过水断面面积，m2;Bk为相应于hk的水面宽度，m。

对于梯形断面，带入(6)，为了试算将其转化为x=g(x)的显式形式，见公式(7)。

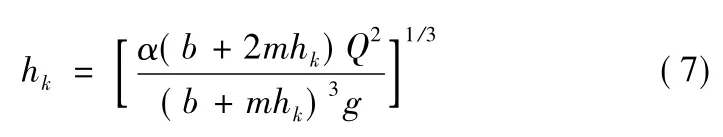
例:Q=79 m3/s，b=15 m，m=3.0，试算临界水深 hk。

首先假设初值 hk0=1.0，带入(8)式校正，得 hc1=1.69687，将hk1带入(8)再校正得，hk2=1.59669，采用埃特金加速迭代公式对hk1进行修正，，再将作为初值进行第二次迭代，至误差满足要求。计算结果见表3。

表3 埃特金迭代加速法求解hk

3 结语

埃特金(Aitken)加速法原理易懂、形式简单、不用求解导数、收敛速度快，是求解水力学方程的有效途径之一。目前埃特金(Aitken)加速法在水力计算中很少被采用，本文介绍了其原理和一般计算步骤，希望对水力计算的试算方法从一个侧面起到引导作用，以提高效率。

［1］李庆扬，王能超，易大义.数值分析(第四版)［M］.北京:清华大学出版社，施普林格出版社，2001.

［2］李炜.水力计算手册(第二版)［K］.北京:中国水利水电出版社，2006.

［3］熊启钧.灌区建筑物的水力计算与结构计算［M］.北京:中国水利水电出版社，2007.