神经元电生理模型的建模方法

任玉强 柴新禹 任秋实 李丽明*

1(上海交通大学生物医学工程学院，上海 200240)

2(北京大学工学院生物医学工程系，北京 100871)

引言

在现代神经科学研究中，探索神经编码、信息传递及处理的生理学机理越来越成为科学工作者关注的焦点。通过数学建模及计算机仿真对神经元及神经元网络进行模拟并揭示其信息编码及传递机理已经成为神经科学家进行科学研究的重要手段。一种具体的实验手段往往只能研究单一层次的问题，而要把许多层次上得到的大量实验数据联系和组织起来并得出定量的规律，对神经系统进行建模及仿真的研究手段发挥了重要的作用。目前，对神经元及神经元网络进行建模的方法有多种，其中，人工神经网络是一种应用类似于大脑神经元突触联接的结构进行信息处理的数学模型，其目的不在于阐明神经信息处理的机制，而在于构建出具有某种特定功能的神经网络模型，以便解决工程上的问题，该内容不在本文的综述范围之内。本文主要对基于神经元生物物理参数进行建模的电生理模型(又称为生物物理模型)的研究方法及进展进行介绍。

神经元电生理模型是指从神经元膜的生物物理性质出发，将神经元分成不同的部分，不同部分彼此耦合起来构成整个神经元及神经元网络的建模方法，其目的是用来阐明神经元及神经元网络的电生理学特性以及信息编码机理。神经元电生理模型可以在多个层次上进行建立，以实验研究结果为基础，采用精细的生物物理参数对单个神经元进行建模，可以研究单个离子通道及受体的功能信息以及单个神经元的兴奋特性及动力学机理，而在多神经元网络的水平上建立的模型，能对神经元间的功能联系及神经信息在神经网络中的传递机制进行研究。例如，不同神经元通常包含了各种不同的离子通道和膜受体，不同种类的离子通道在激活电压、失活电压、电导率等电生理学特性上往往具有显著差异，这种差异性表明不同的离子通道在神经信息的传递中发挥不同的作用，通过对神经元进行电生理建模，就能研究不同种类离子通道在兴奋的产生及传导中所起的作用。

文中将主要从单神经元到局部神经元网络的建模方法、不同模型在神经科学中的应用研究进展以及各种仿真工具等方面进行介绍。

1 建模方法

1.1 霍奇金-赫胥黎模型

现代神经元电生理模型的核心数学框架源自于霍奇金和赫胥黎所建立的模型[1]。通过一系列设计精妙的实验，霍奇金和赫胥黎发现乌贼巨大轴突中离子电流的产生可以用轴突膜中钠离子和钾离子通道电导率的变化来解释，并基于数理科学的知识和方法，建立了钠离子和钾离子通道电导率随膜电位和时间变化的数学模型，进而推导出了导致动作电位产生的一系列微分方程，这就是霍奇金-赫胥黎模型(Hodgkin-Huxley模型、H-H模型)。该模型与实验结果具有高度的一致性，为阐明动作电位是如何产生和传导的这一神经科学基本问题奠定了理论基础，霍奇金和赫胥黎也因此获得了1963年的诺贝尔生理学或医学奖。

1.1.1 等效电路

在基于生物物理学的神经元建模中，神经元的电学特性是通过等效电路来模拟的。用电容来模拟细胞膜的电荷存储能力，用电阻来模拟膜中不同的离子通道，而膜内外离子浓度差异产生的电化学电位用电动势来描述。一小段乌贼巨大轴突的等效电路示意图如图1所示，在等效电路中跨膜电流分为两部分，一部分是通过膜电容的电流，一部分是通过离子通道的电流，在H-H模型中离子电流分为三种：钠电流INa、钾电流IK、主要由氯离子产生的漏电流IL。通过基尔霍夫电流定律可以将图1中的等效电路表示为微分方程：

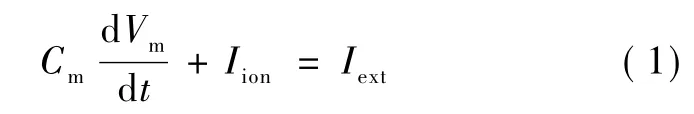
式中，Iext是外部施加的电流，Vm是跨膜电位(Vin-Vout)，该式表示了跨膜电位改变和离子电流之间的关系。

图1 一小段乌贼巨大轴突的等效电路示意图[1]Fig.1 Electrical equivalent circuit for a short segment of squid giant axon[1]

图1中的离子电流代表大量离子通道形成的宏观电流，在模型中宏观电流遵循欧姆定律 I=GV，G代表电导。将此公式代入式(1)中，V就是跨膜电位Vm和平衡电位Ei(i代表不同的离子通道)的差值，整个离子电流就是不同离子通道电流的代数和：

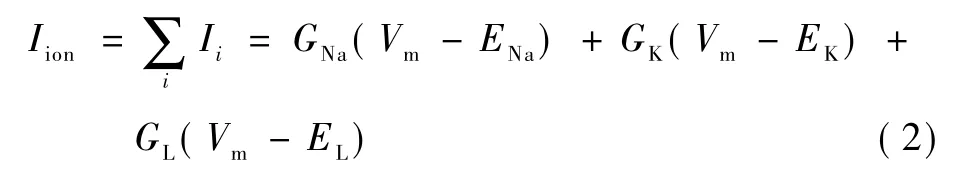
式中，GNa、GK、GL分别代表钠通道、钾通道、漏电流通道的电导，ENa、EK、EL分别代表钠通道、钾通道、漏电流通道的平衡电位。通常，电导都不是常数，而是依赖于膜电位并随时间发生变化。

1.1.2 门控通道

H-H模型中的宏观电导可以看作是镶嵌在膜上众多离子通道共同作用的结果，每个离子通道可以理解为由一个或几个电压门所调控，每个电压门都有两种状态：自由态和非自由态。当一个离子通道的所有电压门都处于自由态时，离子通道打开，离子就能通过离子通道形成离子电流，如果任意一个电压门处于非自由态，离子通道就关闭。

考虑单独的一个电压门 i，定义pi为这个门处于自由态的概率(0～1)。如果考虑大量的电压门，那么pi可以看作是所有的类型为i的电压门中处于自由态的比例，pi(t)就代表在时刻t时处于自由态的电压门比例，1-pi(t)代表处于非自由态的电压门比例。

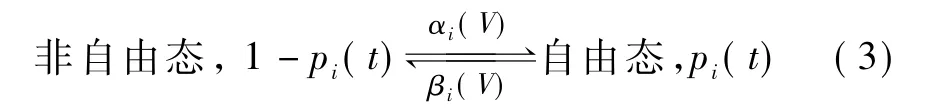
电压门从非自由态转化到自由态的速率为αi(V)，从自由态转化到非自由态的速率为 βi(V)，两种速率都依赖于跨膜电压。在H-H模型中，假定电压门在两种状态间的改变遵循一阶动力学方程：

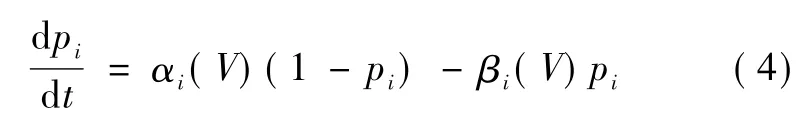
当一个通道开放时，电导会有一定程度的上升，因此大量离子通道形成的宏观电导正比于开放通道的数量，也就正比于相关电压门处于自由态的概率。因此离子通道j的宏观电导Gj正比于组成通道j的所有电压门处于自由态比例的乘积：

式(8)～式(11)以及式(1)合在一起就能够完整描述H-H模型中跨膜电位随时间的变化。为了完整的求解这个模型，必须求出式(9)～式(11)中的6个速率常数。霍奇金和赫胥黎通过电压膜片钳实验，把轴突膜钳制到不同的电压得到电导随时间的变化曲线，通过曲线拟合求得各速率常数的表达式[1]，在此不做进一步介绍。

1.2 钙依赖通道模型

H-H模型中的钠通道和钾通道都是电压门控通道，但某些离子通道同时受跨膜电压和钙离子浓度的影响[2-3]，因此将钙离子浓度整合到 H-H模型中能够更加完整地描述某些神经元的特性。Traub建立的海马区神经元模型中引入了一个代表胞内钙离子浓度的状态变量[4]，这个模型中包含了一种钙依赖的慢钾通道Gs，它的速率常数公式同时依赖于跨膜电压V和胞内的钙离子浓度χ。慢钾通道的电导公式为，其中是慢钾通道的最大电导率，q是一个状态变量，它的一阶动力学方程为

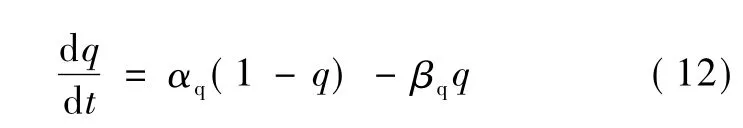
式中，αq和βq是速率常数，其同时依赖于跨膜电压V和胞内钙离子浓度χ：

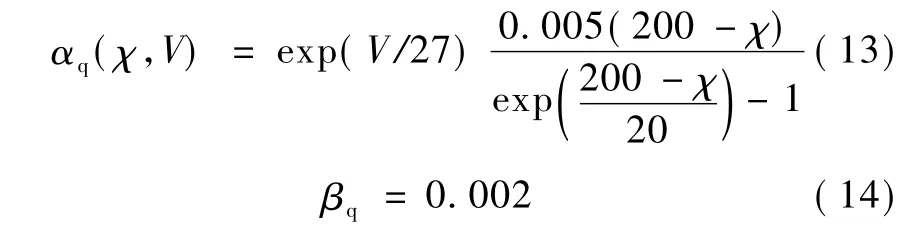
为了理解钙依赖离子通道中钙离子的作用，一般认为在紧靠神经元膜内侧处有一个扁平空间，其中含有大量的钙离子，其浓度要明显高于细胞内其他区域的浓度。钙离子主要通过膜上的钙通道进入这个扁平区域，然后依靠浓度差扩散到胞内其他区域。可以用一个微分方程来模拟胞内钙离子的动力学特性[4]：

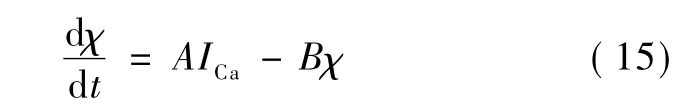
式中，ICa代表钙离子通道形成的钙离子电流，A是一个常数，代表库伦转到离子摩尔量的转换系数，B是速率常数，代表钙离子的扩散速率。

在Traub的研究中建立的包含钙依赖钾通道的CA3海马神经元模型能重现实验中在胞体和顶树突记录到的动作电位，同时也能重现连续刺激下的重复放电现象，从而能够对CA3海马神经元进行更加精确的模拟。

Ekeberg等建立的七鳃鳗运动神经元网络模型中也考虑了钙依赖的钾离子通道[5]，研究发现，钙依赖钾离子电流对动作电位的后超极化时相起主要作用，从而对发放率起到重要的调制作用。Yamada等人对钙依赖通道的机理及建模方法也进行了深入的研究[6]，在此不做详细介绍。

1.3 单离子通道马尔科夫模型

H-H模型对于描述神经元的宏观电流非常成功，然而如果要对单个离子通道电流进行模拟就必须采用其他的方法。在微观层面上，单个离子通道的开放与关闭是一个随机过程，电压门在自由态和非自由态之间的转变依赖于离子通道在不同构型间的变化，特定的构型能使离子通过而其他的构型则不能。通过对单个离子通道进行膜片钳记录，就能观测到离子通道在开放与关闭状态间的随机改变[7-8]。

Destexhe等提出的马尔科夫模型为描述单个离子通道的微观电流提供了理论框架[9]。马尔科夫模型的基本假设是离子通道的关闭与开放，可以被描述为离子通道在一系列不同构型状态间的改变，不同状态间的改变有相应的转移概率。假设离子通道处于状态Si时的概率为Pi(t)，pij为处于状态i的离子通道转移到状态j的条件概率，那么Pi(t)可以表示为：

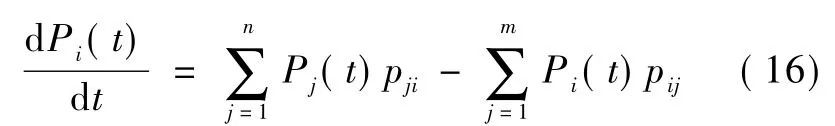
式中右边的第1项代表离子通道由其他状态转移到Si状态时概率的增加量，第2项代表离子通道从状态Si转移到其他状态时概率的减小量。如果有大量相同类型的离子通道，那么Pi(t)可以被解释为离子通道处于状态Si的比率，而pij就可以被解释为不同状态间转变的速率常数。因此通过马尔科夫模型就能够将微观离子通道的特性与H-H模型描述的宏观电流联系起来。

图2表示了一个包含五个状态的马尔科夫模型，这个模型对应了H-H模型中的钾离子通道。该模型中n0状态表示离子通道的四个电压门都处于非自由态，n1状态表示离子通道有一个电压门处于自由态，依次类推，n4状态表示离子通道的四个电压门都处于自由态，此时离子可以通过离子通道。不同状态间的转移概率可以通过H-H模型中的速率常数计算得到，比如从n0状态转移到 n1状态共有4种途径，因此相应的转移概率为4αn。最终单个离子通道所处状态随时间变化的规律可以通过蒙特卡洛模拟得到[9]。

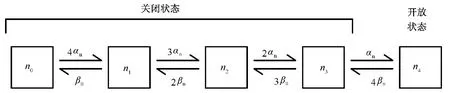
图2 代表H-H模型中钾电导的马尔科夫模型，该模型中的n0到n3为关闭状态，n4为开放状态Fig.2 A Markov model of the HH K+conductance.The Markov model has four closed states n0～ n3 and one open state n4

对于钠离子通道，Destexhe等也通过相同的方法研究[9]。在H-H模型中，假设钠通道的电压门之间都是相互独立的，在马尔科夫模型中也基于该假设进行了研究。但更精细的研究发现钠通道电压门的激活和失活过程并不是完全独立的，因此Patlak提出了一个包含电压门间相互作用的钠离子马尔科夫模型[10]，此模型能更好地对通过膜片钳技术获得的实验数据进行描述。

1.4 突触模型

文中前述内容主要对电压门控离子通道的建模方法进行了介绍，而配体门控的化学突触在神经信号的传递中同样具有重要的作用。当动作电位到达突触前末梢时，神经递质被释放到突触间隙，然后递质与突触后膜的配体门控受体结合导致离子电流流入膜内。

为了模拟突触的活动，一般把突触递质的释放、扩散、与受体结合等一系列细节抽象为突触后的一个时间依赖的配体门控通道，Rall描述了配体门控通道的电导方程[11]。假设在 tspike时刻一个动作电位到达突触，则突触电导方程可表示为：

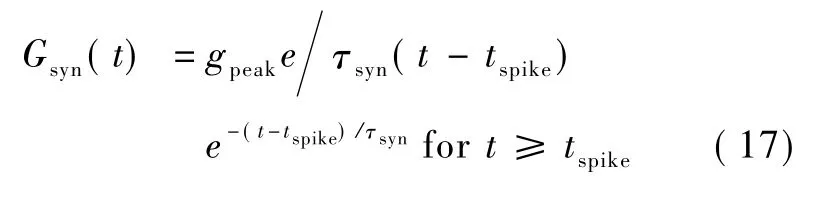
式中，τsyn为时间常数，突触电导在 t=tspike+τsyn时刻达到最大值gpeak，突触产生的突触电流为Isyn(t)=Gsyn(t)(V-Esyn)，其中Esyn为突触的反转电位。

当突触被一系列的动作电位激活时，将每个动作电位引起的电导改变进行代数相加就能得到电导的整体变化，然而这种方法会造成计算复杂性的上升因而很少被用于较复杂的模拟中。有许多有效的方法可以简化计算，比如用二阶动力学方程而不是一阶动力学方程来表示电导的变化[12];或者是重组计算顺序，Sriinaivasan等基于突触配体门控通道模型提出了一种算法，对每个突触只存储相继动作电位产生的电导变化量之和，而不是将所有动作电位产生的电导变化都进行存储再求和[13]，这种算法能提高计算速度，可以用来研究大尺寸神经元网络中短时程突触抑制的集合效应。

另一种对突触电导进行建模的方法是Destexhe等人提出的马尔科夫模型[14]。此模型中的配体门控通道仅仅有开放和关闭两种状态，可以表示为：

式中，C是关闭状态，O是开放状态，T代表神经递质，α和β是速率常数并且独立于跨膜电位。突触电流可表示为：

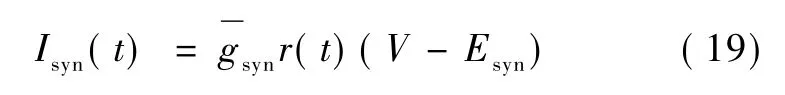
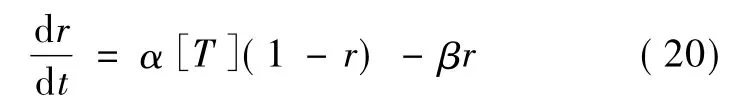
式中，神经递质的浓度为[T]。模拟神经递质浓度的一种简化方法是假定动作电位到达突触前末梢时，递质释放量随时间的变化为幅值不变的脉冲，通过数值计算就能求得r随时间变化的方程[15]。

以上讨论的模型中递质与受体结合会直接导致通道的开放形成离子电流，然而有许多神经元胞体和树突含有代谢型受体，这些受体与递质结合不会导致通道的开放而是激活细胞内的第二信使，经过一系列的胞内生物化学过程最终导致离子通道的开放。对这种级联化学反应可以用马尔科夫模型对每一步电化学反应进行模拟，最后将所有的模型进行整合来实现[15]。

包含突触的神经元模型已经被广泛地应用于神经科学的研究中，Rattay对中枢系统神经元进行了建模，模型中整合了突触模型，用于研究人工电刺激对中枢神经元产生的影响[16]。McIntyre等建立的丘脑皮层中继神经元的模型中包含了兴奋性突触和抑制性突触，此模型被用于深部脑刺激的机理研究中[17]。

1.5 多室模型

图1的等效电路可以用来模拟神经元细胞膜的一个局部区域，然而神经元细胞膜的特性并非各处都是一样的，不同的膜区域可能有不同的几何形状、不同的离子通道种类及数量、不同的受体种类及数量，在神经元的轴突上也可能包裹着髓鞘。多室模型是将神经元在空间上分割成一系列的小室，每个小室具有相同的生物物理学特性，并且可以通过如图1中的等效电路来表示，不同小室等效电路的电学参数根据室与室间生物物理学参数的不同而有所不同，室与室之间通过胞内的轴向电流联系，多室模型的等效电路如图3所示。室i的跨膜电位Vi与相邻室的跨膜电位Vi-1和Vi+1的关系为：

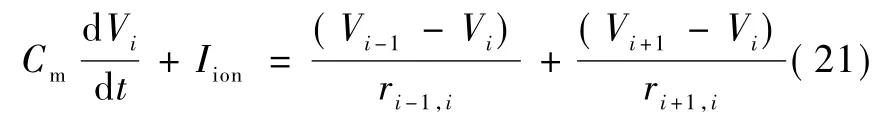
式中，ri±1，i代表相邻室间的胞内轴向电阻，(Vi±1-Vi)/ri±1，i代表胞内轴向电流[18-19]。利用多室模型能够表示任意复杂形状的细胞结构，包括有髓鞘及无髓鞘的神经轴突、复杂的树突、带有分叉的轴突及树突等[20-21]。

图3 单个神经元多室模型的等效电路Fig.3 Electrical equivalent circuit of the compartmental approach for single-neuron modeling

多室模型现在已成为神经科学中电生理模型的重要建模手段，并被广泛地用于神经科学的研究之中。自从Fitzhugh在1962年首次提出神经元有髓鞘轴突的多室模型后[18]，后人对多室模型进行了不断的扩展研究。Durand等在1992年用多室模型研究得出朗飞氏节去极化原因一是来自于朗飞氏节上的激活函数，二是来自于相邻朗飞氏节的电流分布[22]。Foulmeister等在1997年建立了蝾螈视网膜神经节细胞的多室模型，模型中包含了钙离子通道及不同种类的钾离子通道，他们用这个模型研究了神经节细胞的编码机理[23]。Parini等在2000年通过对比不同的多室模型，建立了适合于人类视神经纤维的多室模型，通过与实验数据对比，证实了模型的可行性[24]。McIntyre等在2002年提出了一种双层电缆多室模型，并对哺乳动物的运动神经纤维进行建模[25-26]，此模型对朗飞氏节间包裹着髓鞘的部分进行了精细模拟，模型的特性与实验结果有很好的吻合，他们用此模型研究了哺乳动物运动神经元兴奋时。产生去极化后动作电位和超极化后动作电位的机理，证实了一种慢钾通道在其中起了重要作用，随后在2004年，他们又用这种模型模拟了丘脑中继神经元，并对深部脑刺激的作用机理进行了研究[17]。Rattay等在2004年采用多室模型对视网膜中的双极细胞和神经节细胞进行了建模[27]，模拟结果表明在外部电流下神经节细胞的轴突是首先兴奋的位置。Oozeer等在2005和2006年通过对比前人的多种模型，提出了符合人类视神经纤维的多室模型，通过对外部电极刺激产生的外部电场进行三维仿真，研究了在外部电场作用下视神经纤维的兴奋特性[28-29]。Schiefer等在2006年对单个视网膜神经节细胞进行了建模[30]，研究表明在外部电刺激下神经节细胞首先兴奋的位置是在神经节轴突的弯曲部位。Sotiropoulous等在2007年对McIntyre提出的双层电缆多室模型进行了改进[31]，研究了深部脑刺激中电场对神经元的直接影响。Bellinger等在2008年建立了包含轴突外钾离子浓度变化的有髓鞘神经纤维计算模型[32]，用来研究深部脑刺激的直接作用，仿真结果表明轴突外钾离子的累积会对轴突的兴奋产生功能性的阻断。Jiang等在2009年建立了大鼠丘脑锥体神经元的完整模型[33]，用来研究兴奋性突触和抑制性突触对神经元兴奋共同作用的内在机理，通过模型和实验的研究他们得出了谷氨酸能兴奋性输入和GABA能抑制性输入空间加和作用的数学规律。Morse等在2010年用多室模型建立了丘脑CA1神经元的完整模型[34]，用来研究远端树突引起的超兴奋特性，结果表明动作电位在树突的反向传播导致了超兴奋的产生。

1.6 神经元网络模型

前面几部分介绍了离子通道、突触、单个神经元的建模方法，利用这些方法可以直接建立神经元网络的模型。在神经元网络中神经冲动从一个神经元通过突触连接传递到下一个神经元，通过多室模型对神经元轴突、树突、胞体进行建模，然后通过突触模型模拟突触连接就可以建立整个神经元网络的模型。在建立网络级的模型时，主要考虑两方面的问题，一是要有一种合适的数学方法来描述动作电位在神经元之间的传递，其次是如何确定网络中的突触连接。

在描述动作电位在神经元之间的传递时有两种数学算法，一种称为同步算法(时间驱动算法)[35]，通过这种算法，所有的神经元在每一个时钟时刻都进行一次模拟计算，求得各处的膜电位，这种算法非常适合如基于向量的数值计算工具如Matlab、Scilab等。另一种算法称为异步算法(事件驱动算法)，在这种算法中所有的神经元只在接收到一个动作电位或发放一个动作电位时进行一次模拟计算。异步算法跟同步算法相比更加复杂，它的优势在于当神经冲动没有到达时不需要对每个神经元都进行模拟计算，因此计算速度更快[36-38]。目前，异步算法已经被用于很多复杂的模型中[39-44]。

在建立神经元网络模型时需要考虑的第二个问题是明确神经元之间的连接，小的网络模型可以精确地确定每一个突触连接的细节，然而对大的网络模型就必须采用一定的策略来简化模型。比如无脊椎动物海兔的小的神经网络中仅包含10个神经元，每个神经元有5个突触，总共约有50个突触，因此可以精确地确定每个突触的受体类型、反转电位、最大电导和传导延迟等电生理学特性[45];然而，一个哺乳动物大脑皮层中的局部神经元网络就可能包含一万级别的神经元数量，如果每个神经元有100个突触，总共就会有一百万个突触连接，要精确地确定每个突触连接的细节是非常困难的，必须采用一定的方法来简化模型[46]。一种方法是对于特定种类神经元(比如中间神经元)和一定半径内的另一种神经元(比如皮层锥体神经元)之间的突触连接都采用同一种突触(比如GABA能受体突触)，这样就能极大地简化网络模型，并且能较好地符合生理学结构。

以上介绍的神经元网络的建模方法在需要精确描述动作电位在神经元间的传递时比较有效[47]，然而如果用这种建模方法模拟一个较大的神经元网络时会有巨大的计算量。如果不需要知道神经元的内部机制，而只关心神经元的输入输出关系，则可采用神经元的简化模型构建，比如人工神经网络。这种模型的目的不在于阐明神经回路的机制，而在于构造出具有特定功能的神经网络模型，以解决工程上的实际问题。

2 建模工具

目前已经有复杂的仿真软件工具包来帮助我们实现依赖于生物物理学细节的神经元及网络建模。两种最广泛应用的神经元建模工具为GENESIS(GEneral NEural SImulation System)[48-49]和NEURON[50]。这两种建模环境可以用来建立神经元多室模型，都提供了从分子级别到网络级别的建模工具，并且有预定义的各种功能模块及可视化图形用户界面。功能模块是指依赖于神经元结构特性的各个神经片段、电压门控通道、配体门控通道、化学突触等，通过编程语言将相应的功能模块进行连接就能建立神经元的模型，同时建模工具还提供了模拟膜片钳实验的方法，可以进行各种的模拟实验。目前很多的神经建模工作都是通过GENESIS或NEURON来进行的[51-54]，应用范围包括胞内记录、树突信号传递、神经冲动传导、信息编码以及学习记忆等。

其他较常用的仿真工具还有NEST、NCS、CSIM、XPPAUT、SPLIT和 Mvaspike。NEST主要用于建立大的神经元网络，这个软件可以非常容易地建立105数量级的网络，并且可以在每个神经元加上符合生理学数量的突触[55];NCS适合于对哺乳动物新皮层的神经元结构进行建模;CSIM可以用来模拟多达数千个到十万数量级突触的神经元网络;XPPAUT是一种模拟和分析动态系统的数值计算工具[56];SPLIT是一种专门对基于H-H方程的大规模多室模型进行建模的工具[42];Mvaspike是一种利用事件驱动算法来进行神经元网络建模的工具。概括来说，可以将各种仿真工具依据它们最适宜的应用范围分为四类：(1)单室模型：CSIM、NEST和 NCS;(2)多室模型：NEURON、GENESIS、SPLIT;(3)事件驱动模拟：Mvaspike;(4)动态系统分析：XPPAUT。

3 总结

本文对基于生物物理学参数的神经元电生理模型的建模方法进行了综述，并介绍了采用相关建模方法的研究进展以及常用的建模工具。本文可以为从事神经建模研究的科研人员提供参考。

神经建模作为一种技术手段已经成为神经科学中非常重要的研究方向，已经并将继续为神经科学的研究做出重要贡献。然而，神经建模也有它的局限性，即使建模过程依据了神经元膜的生物物理学特性，这仍是对复杂神经元结构的高度抽象。模型建立的准确性依赖于对重要细节的描述，然而在一种神经元中重要的细节可能在另一种神经元中并不那么重要，因此不能认为神经元模型就是对神经元的完整描述。神经元的建模过程就是一个从实验观察到提出假设(建立模型)，到模型预测(模型仿真)，再到模型检测(同实验数据比较)的不断迭代的过程。

[1]Hodgkin AL， Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve[J].The Journal of Physiology，1952，117(4)：500-544.

[2]Brown AM，Westenbroek RE，Catterall WA，et al.Axonal L-type Ca2+channels and anoxic injury in rat CNS white matter[J].Journal of Neurophysiology，2001，85(2)：900-911.

[3]Stys P，Lopachin R.Mechanisms of calcium and sodium fluxes in anoxic myelinated central nervous system axons [J].Neuroscience，1997，82(1)：21-32.

[4]Traub R.Simulation of intrinsic bursting in CA3 hippocampal neurons[J].Neuroscience，1982，7(5)：1233-1242.

[5]Ekeberg Ö，Wallen P，Lansner A，et al.A computer based model for realistic simulations of neural networks[J].Biological Cybernetics，1991，65(2)：81-90.

[6]Yamada WM，Koch C，Adams PR.Multiple channels and calcium dynamics[M]//Koch C，Segev I.Methods in Neuronal Modeling：From Synapses to Networks.(2nd Edition).Cambridge：MIT Press，1998：137-170.

[7]Neher E，Sakmann B.Single-channel currents recorded from membrane of denervated frog muscle fibres[J].Nature，1976，260(5554)：779-802.

[8]Colquhoun D，Hawkes A.On the stochastic properties of single ion channels[J].Proceedings of the Royal Society of London.Series B，Biological Sciences，1981，211(1183)：205-235.

[9]Destexhe A，Huguenard J.Which formalism to use for modeling voltage-dependent conductances? [M]// Schutter ED.Computational Neuroscience： Realistic Modeling for Experimentalists.Boca Raton：CRC Press，2001：129-157.

[10]Patlak J.Molecular kinetics of voltage-dependent Na+channels[J].Physiological Reviews，1991，71(4)：1047-1080.

[11]Rall W.Distinguishing theoretical synaptic potentials computed for different soma-dendritic distributions of synaptic input[J].Journal of Neurophysiology，1967，30(5)：1138-1168.

[12]Wilson MA，Bower JM.The simulation of large-scale neural networks[M]//Koch C，Segev I.Methods in Neuronal Modeling：From Synapses to Networks.Cambridge：MIT Press，1989：291-334.

[13]Srinivasan R， Chiel HJ. Fast calculation of synaptic conductances[J].Neural Computation，1993，5(2)：200-204.

[14]Destexhe A，Mainen ZF，Sejnowski TJ.Kinetic models of synaptic transmission[M]//Koch C，Segev I.Methods in Neuronal Modeling：From Synapses to Networks(2nd edition).Cambridge：MIT Press，1998：1-26.

[15]Destexhe A，Mainen ZF，Sejnowski TJ.Synthesis of models for excitable membranes，synaptic transmission and neuromodulation using a common kinetic formalism[J].Journal of Computational Neuroscience，1994，1(3)：195-230.

[16]Rattay F.Analysis of the electrical excitation of CNS neurons[J].IEEE Transactions on Biomedical Engineering，1998，45(6)：766-772.

[17]McIntyre C，Grill W，Sherman D，et al.Cellular effects of deep brain stimulation：model-based analysis of activation and inhibition[J].Journal of Neurophysiology，2004，91(4)：1457-1469.

[18]Fitzhugh R.Computation of impulse initiation and saltatory conduction in a myelinated nerve fiber[J]. Biophysical Journal，1962，2(1)：11-21.

[19]McNeal D.Analysis of a model for excitation of myelinated nerve[J].IEEE Transactions on Biomedical Engineering，1976，23(4)：329-337.

[20]Segev I.Cable and compartmental models of dendritic trees[M]//Bower JM，Beeman D.The Book of GENESIS：Exploring Realistic Neural Models with the General Neural Simulation System.New York：Springer-Verlag，1998：51-77.

[21]Zhou XL， Chiu XS. Computer model for action potential propagation through branch point in myelinated nerves[J].Journal of Neurophysiology，2001，85(1)：197-210.

[22]Durand D.Modeling the effects of electric fields on nerve fibers：determination of excitation thresholds [J].IEEE Transactions on Biomedical Engineering，1992，39(12)：1244-1254.

[23]Fohlmeister J， Miller R. Impulse encoding mechanisms of ganglion cells in the tiger salamander retina[J].Journal of Neurophysiology，1997，78(4)：1935-1947.

[24]Parrini S，Delbeke J，Legat V，et al.Modelling analysis of human optic nerve fibre excitation based on experimental data[J].Medical and Biological Engineering and Computing，2000，38(4)：454-464.

[25]McIntyre C，Richardson A，Grill W.Modeling the excitability of mammalian nerve fibers：influence of afterpotentials on the recovery cycle[J].Journal of Neurophysiology，2002，87(2)：995-1006.

[26]McIntyre CC，Grill WM.Extracellular stimulation of central neurons：influence of stimulus waveform and frequency on neuronal output[J].Journal of Neurophysiology，2002，88(4)：1592-1604.

[27]Rattay F， Resatz S. Effective electrode configuration for selective stimulation with inner eye prostheses[J]. IEEE Transactions on Biomedical Engineering，2004，51(9)：1659-1664.

[28]Oozeer M，Veraart C，Legat V，et al.Simulation of intra-orbital optic nerve electrical stimulation[J].Medical and Biological Engineering and Computing，2005，43(5)：608-617.

[29]Oozeer M， Veraart C， Legat V， et al. A model of the mammalian optic nerve fibre based on experimental data[J].Vision Research，2006，46(16)：2513-2524.

[30]Schiefer M，Grill W.Sites of neuronal excitation by epiretinal electrical stimulation [J].IEEE Transactions on Neural Systems and Rehabilitation Engineering，2006，14(1)：5-13.

[31]Sotiropoulos S，Steinmetz P.Assessing the direct effects of deep brain stimulation using embedded axon models[J].Journal of Neural Engineering，2007，4(2)：107-119.

[32]Bellinger SC，Miyazawa G，Steinmetz PN.Submyelin potassium accumulation may functionally block subsets of local axons during deep brain stimulation：a modeling study[J].Journal of Neural Engineering，2008，5(3)：263-274.

[33]Hao J，Wang XD，Dan Y，et al.An arithmetic rule for spatial summation of excitatory and inhibitory inputs in pyramidal neurons[J].Proc Natl Acad Sci USA，2009，106(51)：21906-21911.

[34]Morse TM， Carnevale NT， Mutalik PG， et al.Abnormal excitability of oblique dendrites implicated in early alzheimer's：a computational study [J].Front Neural Circuits，2010，4(16)：1-11

[35]Rotter S，Diesmann M.Exact digital simulation of time-invariant linear systems with applications to neuronal modeling[J].Biological Cybernetics，1999，81(5)：381-402.

[36]Fujimoto RM.Parallel Simulation： Parallel and Distributed Simulation Systems[M].New York：Wiley，2001：147-157.

[37]Zeigler BP，Praehofer H，Kim TG.Theory of Modeling and Simulation[M].(2 nd Edition).New York：Academic Press，2000.

[38]Sloot P， Kaandorpa JA， Hoekstra G， et al.. Distributed simulation with cellular automata：Architecture and applications[C]//Pavelka J，Tel G，Bartosek M，eds.SOFSEM’99：Theory and Practice of Informatics.Berlin：Springer-Verlag，1999：203-248.

[39]Makino T.A discrete-event neural network simulator for general neuron models[J].Neural Computing ＆ Applications，2003，11(3)：210-223.

[40]Gerstner W，Kistler WM.Mathematical formulations of Hebbian learning[J].Biological Cybernetics，2002，87(5)：404-415.

[41]Djurfeldt M，Johansson C，Örjan Ekeberg R.Massively parallel simulation of brain-scale neuronal network models[R].TRITA-NA-P0513，2005.

[42]Brette R.Exact simulation of integrate-and-fire models with exponential currents[J].Neural Computation，2007，19(10)：2604-2609.

[43]Izhikevich EM.Simple model of spiking neurons [J].IEEE Trans Neural Networks，2003，14(6)：1569-1572.

[44]Brette R，Gerstner W.Adaptive exponential integrate-and-fire model as an effective description of neuronal activity[J].Journal of Neurophysiology，2005，94(5)：3637-3642.

[45]White JA，Ziv I，Cleary LJ，et al.The role of interneurons in controlling the tail-withdrawal reflex in Aplysia：a network model[J].Journal of Neurophysiology，1993，70(5)：1777-1786.

[46]Wang Xiaojing， Buzsaki G.Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model[J].J Neurosci，1996，16(20)：6402-6413.

[47]Manor Y， Gonczarowski J， Segev I.Propagation of action potentials along complex axonal trees.Model and implementation[J].Biophysical Journal，1991，60(6)：1411-1423.

[48]Bower JM，Beeman D，Wylde AM.The book of GENESIS：exploring realistic neural models with the GEneral NEural SImulation System[M].New York：Springer-Verlag，1998.

[49]Bower JM，Beeman D，Hucka M.GENESIS simulation system[M]//The Handbook of Brain Theory and Neural Networks.(2 nd Edition).Cambridge：MIT Press，2002：475-478.

[50]Hines ML， Carnevale NT. The NEURON simulation environment[J].Neural Computation，1997，9(6)：1179-1209.

[51]Botta P，de Souza FMS，Sangrey T，et al.Alcohol excites cerebellar golgi cells by inhibiting the Na+/K+ATPase [J].Neuropsychopharmacology，2010，35(9)：1984-1996.

[52]Hendrickson E，Edgerton J，Jaeger D.The capabilities and limitations of conductance-based compartmental neuron models with reduced branched or unbranched morphologies and active dendrites[J].Journal of Computational Neuroscience，2011，30(2)：301-321.

[53]Edgerton JR，Hanson JE，Gunay C，et al.Dendritic sodium channels regulate network integration in globus pallidus neurons：a modeling study[J].J Neurosci，2010，30(45)：15146-15159.

[54]Uebachs M，Opitz T，Royeck M，et al.Efficacy loss of the anticonvulsant carbamazepine in mice lacking sodium channel beta subunits via paradoxical effects on persistent sodium currents[J].J Neurosci，2010，30(25)：8489-8501.

[55]Morrison A， Mehring C， Geisel T， et al. Advancing the boundaries of high-connectivity network simulation with distributed computing [J].Neural Comput，2005，17(8)：1776-801.

[56]Ermentrout B. Simulating， Analyzing， and Animating Dynamical Systems：A Guide to XPPAUT for Researchers and Students[M].Philadelphia：SIAM，2004.