几种混凝土弹性模量理论计算方法精度比较

王伟成，高利甲

（1.中煤三建，宿州234000；2.天津华汇建筑工程设计有限公司，天津300384）

0 引 言

目前通过试验方法获得弹性模量比较烦琐，需要反复加载卸载，直至前后两次的变形差稳定，期间人工干预比较大，结果难以准确；所以，有关学者提供了多种弹性模量计算模型，本文就这些模型的精度进行分析，以更好的与试验相结合来指导工程实践.

1 弹性模量理论计算模型

弹性模量作为混凝土的一个重要的力学参数，国内外对其进行过大量的研究.基于复合材料理论，国外学者提出多种计算模型系统，具体如下；

1.1 并联（Voigt）和串联（Reuss）系统［1］［2］

并联和串联系统是两种极端的排列方式：并联系统中，两相材料承受相同的应变，计算了弹性模量的上限解；串联系统中，两相材料承受相同的应力，计算了弹性模量的下限解.但实际工程中，混凝土各组分既不是承受相同应力，也不是承受相同的应变，所以V－R模型不够精确.模型如图1所示，表达式如公式（1）、（2）.

式中：Ec——混凝土的弹性模量

Ep——水泥砂浆的弹性模量

Ea——骨料的弹性模量

Vp——水泥浆体的体积百分数

Va——骨料的体积百分数

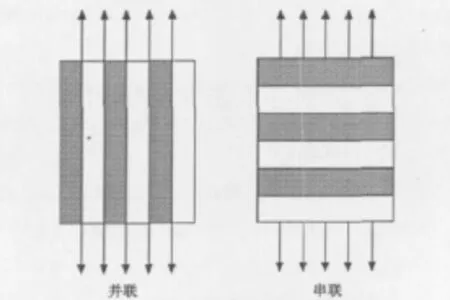
图1 并联与串联模型系统

1.2 Hirsch模型系统［1］［2］

Hirsch模型系统是将并联和串联模型进行组合得到的一个新模型，x为加权因子，混凝土的x近似值为0.5.模型如图2，表达式如公式（3）.

图2 Hirsch模型系统

1.3 H－S（Hashin－Shtrikman）系统模型［1］［2］

H－S系统模型比其他模型计算要精确一些；具体表达式如公式（4）～（13）.

其中：E——弹性模量

K——体积模量

G——剪切模量

n——泊松比

V——各组分的体积百分数

m——水泥砂浆

a——骨料

c——混凝土

（－）——下限值

（＋）——上限值

2 弹性模量数值计算值及其与理论的结果的比较

本节通过建立一组（3个）随机骨料混凝土数值模型，见图3.通过调节混凝土的水胶比（0.26～0.55），使用ANSYS软件计算其应力应变全曲线，然后获得初始切线模量、33%割线模量及峰值割线模量，进而与上节中的三种弹性模量理论计算值进行比较，得出30组数据，结果见表1；对计算结果进行误差分析如图4所示.

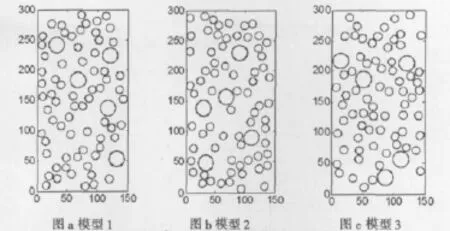
图3 混凝土棱柱体模型

表1 数值计算结果与理论计算结果比较

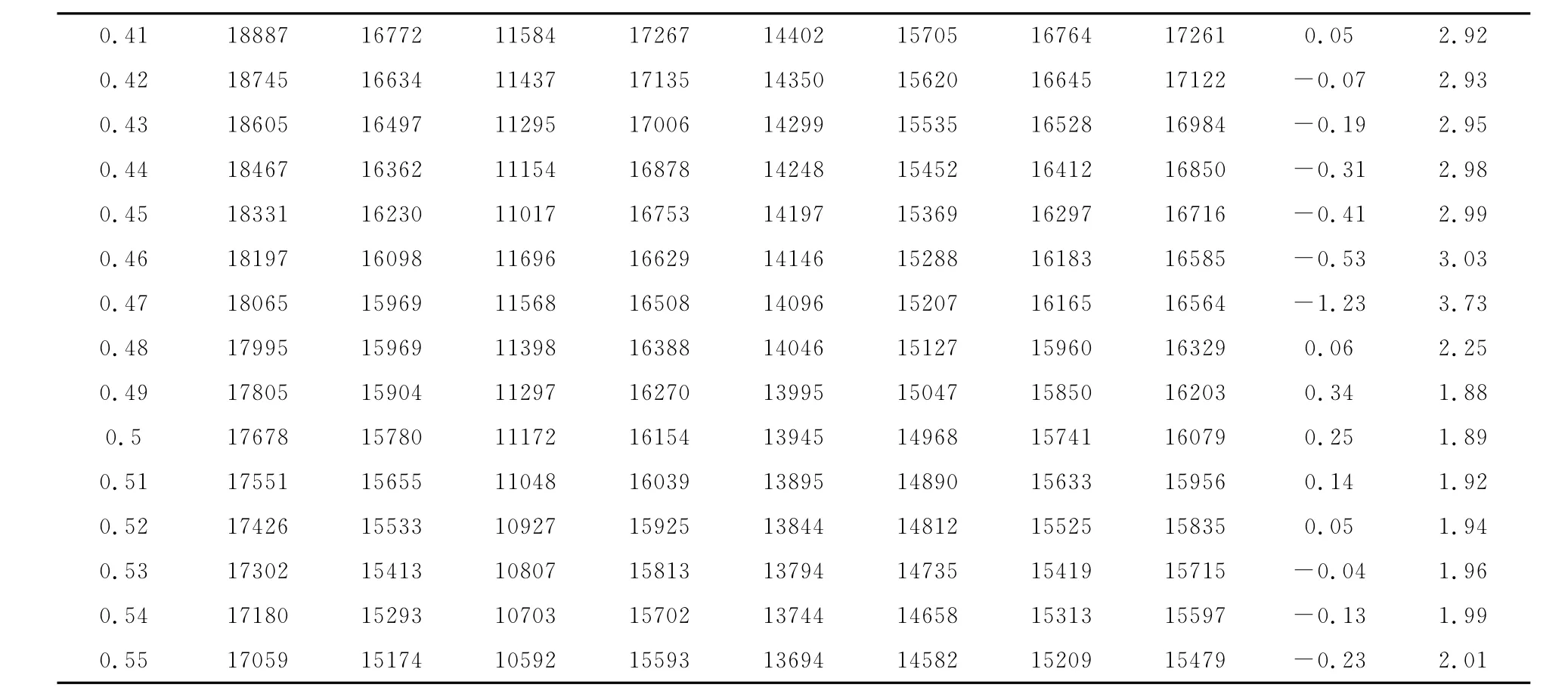
0.41 18887 16772 11584 17267 14402 15705 1676417261 0.05 2.92 0.42 18745 16634 11437 17135 14350 15620 16645 17122 －0.07 2.93 0.43 18605 16497 11295 17006 14299 15535 16528 16984 －0.19 2.95 0.44 18467 16362 11154 16878 14248 15452 16412 16850 －0.31 2.98 0.45 18331 16230 11017 16753 14197 15369 16297 16716 －0.41 2.99 0.46 18197 16098 11696 16629 14146 15288 16183 16585 －0.53 3.03 0.47 18065 15969 11568 16508 14096 15207 16165 16564 －1.23 3.73 0.48 17995 15969 11398 16388 14046 15127 15960 16329 0.06 2.25 0.49 17805 15904 11297 16270 13995 15047 15850 16203 0.34 1.88 0.5 17678 15780 11172 16154 13945 14968 15741 16079 0.25 1.89 0.51 17551 15655 11048 16039 13895 14890 15633 15956 0.14 1.92 0.52 17426 15533 10927 15925 13844 14812 15525 15835 0.05 1.94 0.53 17302 15413 10807 15813 13794 14735 15419 15715 －0.04 1.96 0.54 17180 15293 10703 15702 13744 14658 15313 15597 －0.13 1.99 0.55 17059 15174 10592 15593 13694 14582 1520915479 －0.23 2.01

图4 误差分析图

从表1和图4可以看出：

（1）V－R模型结果范围太大，不能很好的对弹性模量进行估算.其上限值可以较好的估算混凝土的弹性模量值.

（2）Hirsch模型计算结果整体偏小.

（3）H－S模型计算结果范围比较小，可以准确的估算出弹性模量，该模型最为理想.通过分析误差得：数值计算得出的弹性模量结果与H－S模型的下限值最为接近，说明该模型的下限值更能真实的反应材料的弹性模量.

3 结 论

（1）通过以上可以得出三种弹性模量计算方法可以估算混凝土弹性模量，而对其初始切线模量和峰值割线模量分析效果欠佳.

（2）H－S模型可以准确的估算出混凝土的弹性模量，该模型最为理想，其下限值更能真实的反应混凝土的弹性模量.

［1］ 过镇海，时旭东.钢筋混凝土原理与分析［M］.清华大学出版社，2003.

［2］ Peter Simeonov and Shuaib Ahmad.Effect of Transition Zone of the Elastic Behavior of Cement－based Composites［J］.Coment and Concrete Research.1996，26（4）：611－622.