CFD结合遗传算法优化室内热舒适性参数
孙 斌,蒋能飞,韩 克,周 妍
(东北电力大学 能源与动力工程学院,吉林 吉林132012)
人的一生70%以上的时间是在室内度过的,室内空气环境的好坏不仅关系到人的舒适与健康,还会影响人的工作效率,良好的室内空气流动形式是实现室内合理温度、湿度、风速和污染物分布的基础,尤其是目前在特别强调节能的大环境下,如何既能保障室内空气环境的需要,又能最大限度地节约创造室内空气环境的能耗,是从事室内空气环境研究和创造的人士面临的重要课题[1]。目前,室内空气质量的研究主要采用现场调查、实验测试和数值模拟方法,而这些方法都难以对模型进行优化,于是人们提出在遗传算法中直接调用CFD程序,但这种方法计算量相当大的,在使用遗传算法进行搜索时,每搜索一次,需要CFD程序运行超过5000次(遗传算法种群数为100),需要迭代计算十多个小时才能达到收敛[2]。为了解决上述问题,文章应用BP神经网络建立了一个替代模型,该模型首先采用CFD模拟软件建立教室模型,通过CFD模拟得到室内空气温度、相对湿度、平均辐射温度、空气速度、送风口与取样点的距离、PMV值和空气年龄的数据,然后应用CFD模型产生的数据建立BP神经网络模型来取代CFD模型,并根据热舒适性指标PMV值和空气龄数据建立遗传算法的目标函数,设置不同的权重,得到室内参数的最优值,根据优化的参数值调整教室模型,最后并与原CFD模型相比较。
1 热舒适性评价
1.1 PMV指标
PMV指标是众多评价热舒适性指标的一种,已经通过国际标准化组织(ISO 7730)的认可,具有科学性和实用性,PMV指标是丹麦教授Fanger在建立人体两点间热平衡模型的基础上,通过收集受试者的冷热感觉反映之后,利用回归公式使其量化后得到的[3],PMV指标与人的新陈代谢率、衣服热阻、空气温度、相对湿度、平均辐射温度、空气流速有关,它们之间有如下关系[4-5]:
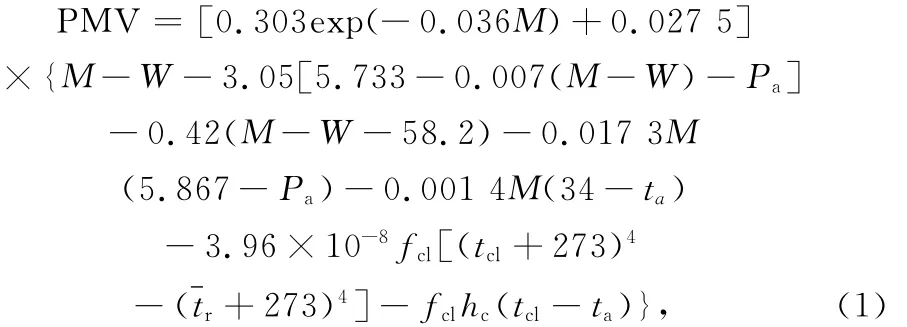
式中:M为人体能量代谢率,决定于人体的活动量大小,W/m2;fcl为人体着装后的实际表面积和人体裸身表面积之比,即服装的表面系数;W 为人体所做的机械功 W/m2;ta为人体周围空气温度,℃;Pa为人体周围空气的水蒸气分压力,Pa;tcl为人体外表面温度,℃为房间的平均辐射温度,℃;hc为对流换热系数,W/(m2·℃)。
Fanger又将PMV指标具体分成7个指标,见表1所示。

表1 PMV指标值
1.2 空气龄
空气龄是指空气进入房间的时间。在房间内污染物源分布均匀且送风为全新风时,某点的空气龄越小,说明该点的空气越新鲜,空气品质就越好。它还反映了房间排除污染物的能力,平均空气龄小的房间,去除污染物的能力就强。由于空气龄的物理意义明显,因此作为衡量空调房间空气新鲜程度与换气能力的重要指标,其表达式为[1]:

其中:F(τ)是年龄比τ短的空气微团所占的比例,τp是某点的空气龄在该点所有微团的空气龄的平均值。
2 模型的建立
2.1 建立CFD模型
建立的教室CFD模型如图1所示。教室的尺寸为8.8m×7.8m×3.9m,室内放置了42张课桌,桌前均坐着一个人:1.73m ×0.3m×0.2m,58.2W/m2;教室里有两扇窗户,尺寸均为3.8m×2.2m,壁面温度均为33.9℃;该模型起初采用侧送侧回的方式送风,2个送风口,1个回风口,送、回风口的尺寸均为0.4m×0.32m,其中送风口的送风温度为17.6℃,速度为2.02m/s。教室内布置了12盏灯,灯的尺寸为0.2m×1.2m×0.15m,功率为60W。
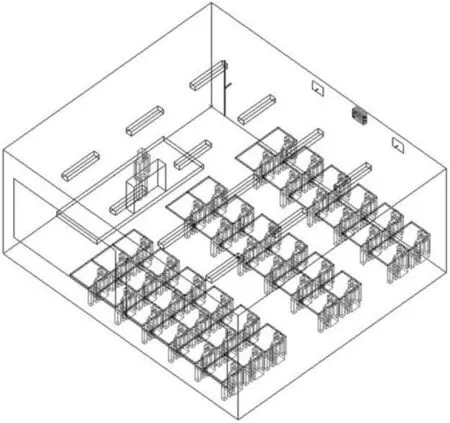
图1 教室的CFD模型
假设教室的CFD模型室内气体为不可压缩且符合Boussinesq假设,气流的流动为低速不可压缩稳态湍流[6],依据当地气候资料,夏季空调室外温度为33.9℃,教室室内设计温度为26℃,相对湿度为60%,模型中设有一面外墙,其他均为内墙,屋顶和地板为绝热边界层,外墙对面的墙有一扇门,考虑了漏风的影响,假设门开启一定角度。根据以上说明得其控制方程为[1]:
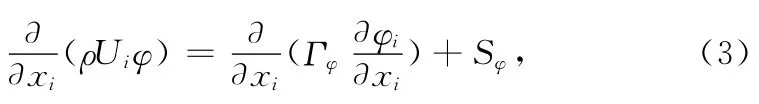
式中:φ为通用变量,可以代表u,v,w,T等求解变量;Γφ为广义扩散系数;Sφ为广义源项。应用CFD模拟软件,采用六面体网格进行网格划分,对该CFD模型进行模拟,当CFD模型计算达到收敛之后,取出模型的255组数据,其中数据均为人体胸部的高度(1.1m高处),D为送风口与取样点的距离,部分数据如表2所示。

表2 室内参数
从表2可以看出,如果风口按该模型布置,则1.1m高处的室内温度在24.54℃~27.66℃,PMV值在之间0.45~2.02之间,根据《采暖通风与空气调节设计规范》(GB50019-2003)中规定:PMV值宜在-1~+1之间,显然达不到要求,而且温度和PMV分布也很不均匀,靠近风口的座位感到适中,而远离风口的座位却感觉到热,室
内总体感觉不舒适,从而影响了学生的学习效率,因此需要对室内的控制参数进行合理的优化。
2.2 建立BP网络模型
在BP网络中,网络的学习过程实质上是一种误差修正的算法,这种学习算法由正向传播和反向传播组成[7-8]。采用误差逆转传播算法,即BP算法建立一个3层神经网络模型,该神经网络模型5个输入量:空气温度、相对湿度、平均辐射温度、空气速度和送风口与取样点的距离D,2个输出量:PMV指标及空气年龄。隐层的神经元数目选择是一个十分复杂的问题,本文根据Kolmogorov定理进行计算[9]为:
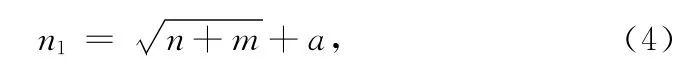
式中:n1为隐层的神经元数;n和m分别为样本的输入和输出神经元数;a为[1,10]之间的常数。文中用235组建立BP模型,20组数据来评价该网络的计算准确性。训练采用Levenberg-Marquardt反向传播算法,通过比较不同隐层节点数的误差和训练步数,最终确定隐层数为8,隐层神经元的传递函数为Signoid型正切函数tansig,输出层的传递函数为Signoid型对数函数logsig,训练次数设为1 000次,建立的BP神经网络模型如下图2所示。
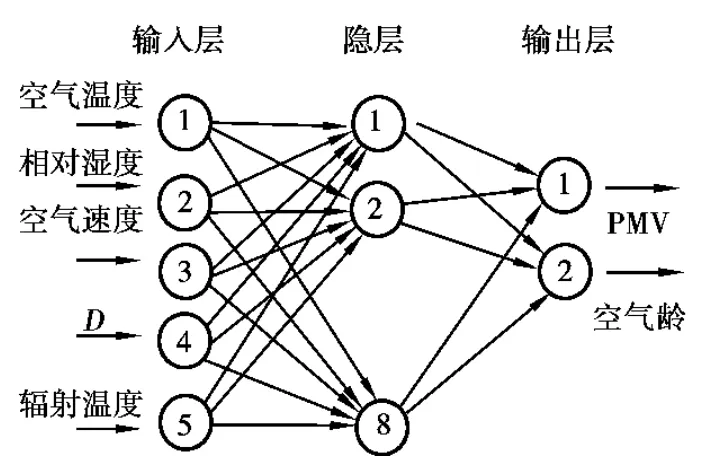
图2 BP网络结构图
将数据的计算值与预测值进行比较得出,PMV指标的均方差为4.96×10-4,平均绝对误差为0.016 2,最大绝对误差为0.179 0,而空气龄的均方差为5.29×10-4,平均绝对误差为0.017 7,最大绝对误差为0.136 4,由这些误差值可以看出,BP神经网络所建立的模型精度很高,可以很好地代替CFD模型。
3 遗传算法寻优
与传统的优化算法相比,遗传算法(GA)是从多个点构成的群体进化搜索,搜索最优解过程中只需要目标函数值转换为适应度信息,搜索过程不易陷入局部最优点[10],因此,本文采用遗传算法,选用浮点编码,设定初始种群大小为20个,交叉概率为0.8,变异概率为0.2,种群数为100,其寻优的流程图如下图3所示,其中本文的目标函数采用权重系数变化法,即对于一个多目标优化问题,若给其每个子目标函数f(xi)(i=1,2,…,n)赋予权重wi(i=1,2,…,n),其中wi为相应f(xi)的在多目标优化问题中的重要程度,则各个子目标函数的线性加权和表示为[11]:

其中,u作为多目标函数的评价函数,则多目标优化问题就可以转变为单目标优化问题。而对于本文涉及PMV指标及空气龄的优化,其目标函数可以定义为[12-14]:

式中,X为输入变量(空气温度、相对湿度、平均辐射温度、空气速度和送风口与取样点的距离D),w1为PMV值的权重,w2为空气龄的权重,PT为惩罚函数,下表i为变量的位置,其中w1,w2可以根据使用者的个人情况或者理性的分析之后给出不同的值,通过不断调整得到最优的情况。本文通过一组使人感觉舒适的数据作为参考基准,通过不同的w1和w2来与参考基准作比较得出优化结果,如表3所示。
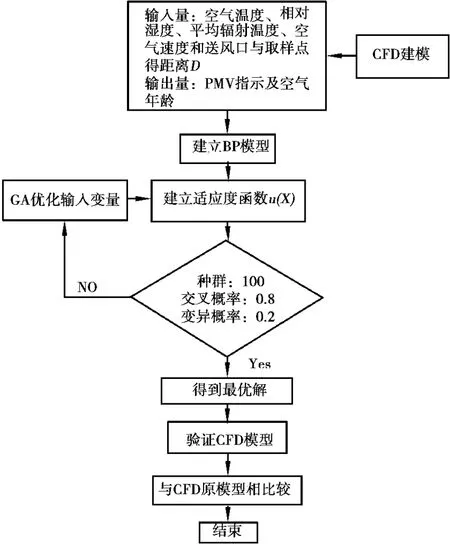
图3 CFD结合遗传算法的流程图
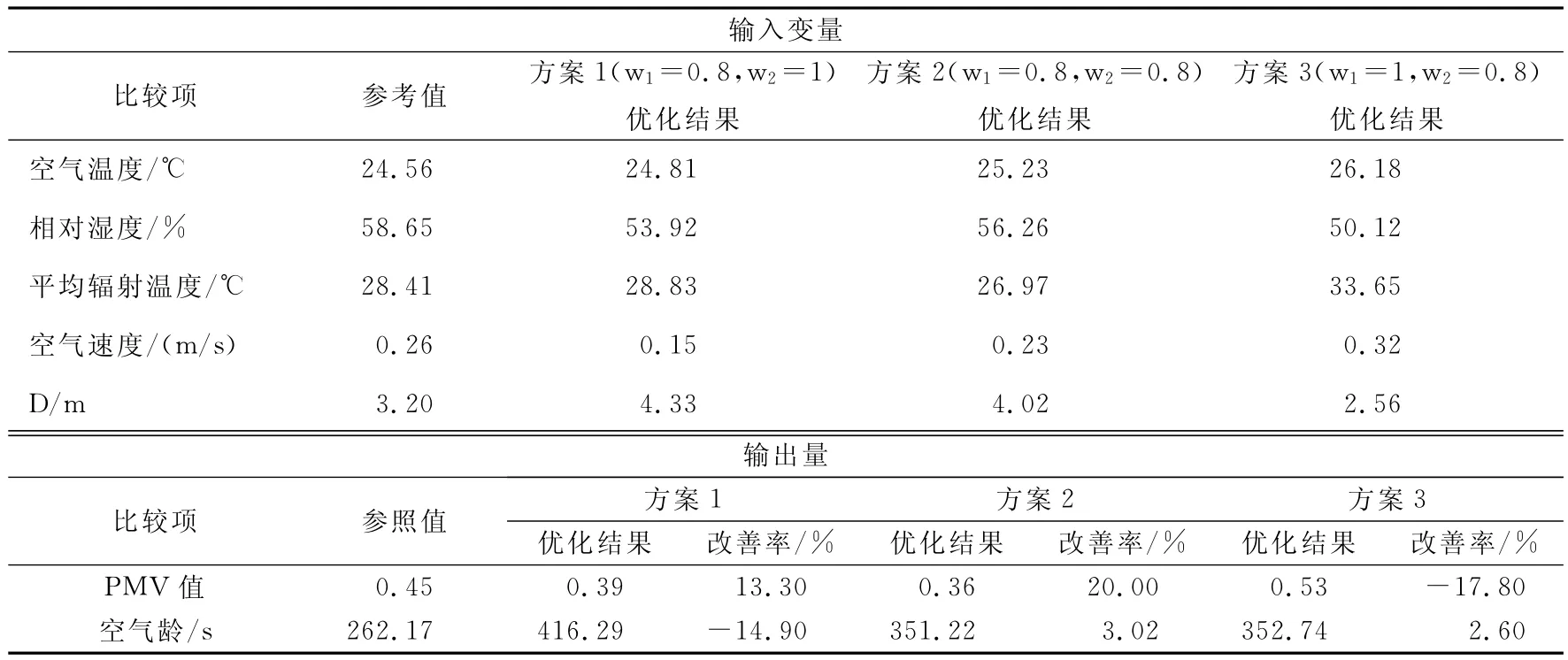
表3 权重的影响
表3中,改善率为正时,表示室内空气品质得到改善,反之,则变差。从表中可以看出,方案1室内热舒适得到改善,但室内空气质量与参考基准相比较,变的不新鲜,方案2中室内空气质量也得到了改善,而方案3恰恰与方案1相反,室内空气质量得到改善,而室内热舒适性相对降低,因此方案2更适合教室模型参数的控制调节。根据优化的结构,重新布置空调送风口的位置,将原来的侧送风改回上送上回式,每个送风口的离周围学生的座位的距离大约4m,尺寸均为0.4m×0.32m,送风速度为1.01m/s,共4个。其中回风口的位置及尺寸不变。将重新布置的模型进行模拟计算,均匀的取出25组数据(PMV值和空气龄)与原数据做比较,如图4、5所示。从图4、图5可以看出,教室内的热舒适及空气龄除个别点外都得到了改善,使教室的空气质量得到了提高,学生在教室学习更加的舒适,提高了学习效率。
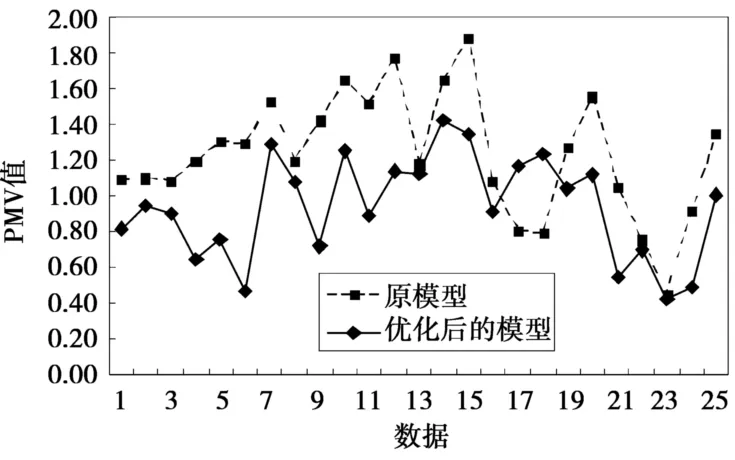
图4 优化前后的PMV值

图5 优化前后的空气龄
4 结 论
本文应用CFD结合遗传算法优化室内空气品质,通过CFD模拟得到的数据作为BP网络的输入输出,通过BP网络建立输入量和输出量的关系模型,从而得到它们之间的复杂函数关系,然后采用遗传算法对建立的函数关系进行优化并与原模型做了比较,结果表明,优化后的模型室内空气品质得到了改善,该模型可以很好地替代用遗传算法中直接调用CFD程序优化的模型,并且CFD耦合遗传算法的模型所消耗的时间只有2~3h,缩短了实验周期,改善了教室的室内空气质量,也提高了学生的学习效率。
[1]李先庭,赵彬.室内空气流动数值模拟[M].北京:机械工业出版社,2009.
[2]徐巍,陈祥光,彭红星.基于神经网络和遗传算法优化室内热舒适控制参数[J].北京理工大学学报,2010,30(2):240-244.XU WEI, CHEN XIANG-GUANG, PENG HONG-XING.Optimization of the control variables of indoor thermal comfort based on genetic algorithm and neural network[J].Transactions of Beijing Institute of Technology,2010,30(2):240-244.
[3]张川燕,王子介.基于BP神经网络的热舒适性指标计算[J].南京师范大学学报:工程技术版,2009,9(1):44-48.ZHANG CHUAN-YAN, WANG ZI-JIE.Thermal comfort index computing based on BP neural networks[J].Journal of Nanjing normal university(Engineering And Technology Edition),2009,9(1):44-48.
[4]朱颖心.建筑环境学[M].第2版.北京:中国建筑工业出版社,2005.
[5]ISO 7730-2005.Ergonomics of the Thermal environment-analytical determination and interpretation of thermal comfort using calculation of the PMVand PPDIndices and local thermal comfort criteria[S].British:International Standard Organization,2005.
[6]G.M.STAVRAKAKIS,D.P.KARADIMOU,P.L.ZERVAS,et al.Selection of window sizes for optimizing occupational comfort and hygiene based on computational fluid dynamics and neural networks[J].Building and Environment,2011(46):298-314.
[7]王剑,王昭俊,郭晓男.基于神经网络的哈尔滨高校教室热环境特征模型研究[J].建筑科学,2009,25(8):89-93.WANG JIAN,WANG ZHAO-JUN,GUO XIAO-NAN.Study on characteristic model for thermal environment of university classrooms based on neural network in Harbin[J].Building Science,2009,25(8):89-93.
[8]赵博,连之伟,周湘江,等.基于神经网络的室内热舒适评判模型[J].哈尔滨工业大学学报,2003,35(12):1436-1438.ZHAO BO,LIAN ZHI-WEI,ZHOU XIANG-JIANG,et al.Evalution model for indoor thermal comfort based on neural network[J].Journal of Harbin Institute of Technology,2003,35(12):1436-1438.
[9]飞思科技产品研发中心.神经网络理论与MATLAB7实现[M].北京:电子工业出版社,2006.
[10]谢怀勤,沈军,丛培海.人工神经网络结合遗传算法对CFWRP固化制度的优化[J].玻璃钢/复合材料,2007(2):3-6.XIE HUAI-QIN,SHEN JUN,CONG PEI-HAI.Optimization of curing cycle of CFWRP with combination of artificial neural network and genetic algorithm[J].FRP/CM,2007(2):3-6.
[11]雷英杰,张善文,李继武,等.MATLAB遗传工具箱及应用[M].西安:西安电子科技大学出版社,2005.
[12]LIANG ZHOU,FARIBORZ HAGHIGHAT.Optimization of ventilation system design and operation in office environment,part I:methodology[J].Building and Environment,2009(44):651-656.
[13]ROBERTO Z.FREIRE,GUSTAVO H.C.OLIVEIRA,NATHAN MENDES.Predictive controllers for thermal comfort optimization and energy savings[J].Energy and Buildings,2008(40):1353-1365.
[14]TAEYEON KIM,DOOSAM SONG,SHINSUKE KATO,et al.Two-step optimal design method using genetic algorithms and CFD-coupled simulation for indoor thermal environments[J].Applied Thermal Engineering,2007(27):3-11.

