应用灰关联分析林边溪溃堤淤积土壤分层

叶一隆，黄俊严，邹 祎

（国立屏东科技大学 土木工程系，台湾 屏东91201）

2009年8月7日，中度台风莫拉克所引进的西南气流带来豪大雨，导致台湾南部与东部县市严重水患，尤其以屏东县林边乡及佳冬乡最为严重。因豪雨致使林边溪上游坡地多处崩塌，而使漂流木及泥砂夹杂于洪流中冲击下游结构物，使林边溪下游多处堤岸被冲毁，洪水夹带大量的泥砂冲入村内，淤泥积深严重阻塞排水设施，严重瘫痪排水系统，也造成道路及维生系统瘫痪[1]。然而，灾害发生后，为急速复原以利民众恢复正常作息，破堤所产生的淤积亦被快速清除，无法等待开挖剖面确认淤泥淤积深度及进行相关量测试验，为建立未来灾害仿真所需数据，笔者在破堤处附近的田区分层取样，利用灰关联分析淤泥淤积深度。

灰色系统理论（Grey System Theory）是邓聚龍于1982年所提出[2]，此理论包括灰色预测、灰关联分析、灰色统计等。灰关联分析应用于水利工程相关研究，叶一隆等[3]应用灰关联分析方法探讨影响休耕水田蓄水区位评估因子，包括取水距离、土壤入渗率、调洪效益与水田灌溉面积4种评估因子，估算出该区域中最适合当休耕水田蓄水之区位。叶一隆[4]利用灰关联分析来推估位于屏东市的高雄区农业改良场雨量测站1929—1999年的观测雨量的重现几率。黄皇嘉等[5]利用灰关联分析来探讨不同大小降雨量产生入渗至地表下不同深度前所需的时间及到达浅层含水层地下水位面所需的时间。Wong等[6]建立了灰色关联的方法来测试变异点的水文数据。Trivedi等[7]指出数学模型用于仿真水文过程一般需要比较长的时间数据系列，在无法获得可靠且长久的水文数据状况下，应用灰色系统理论来发展径流预测模型。Yu等[8]应用灰色系统理论与模糊理论来进行降雨预测。Ip等[9]指出GRM是一个有用的工具，用于分析不精确的数据，样品和不完整的短水文数据。Yeh等[10]应用灰关联分析来评估于屏东平原境内的4个最佳人工湖泊地点。Mujumdar[11]应用灰色模糊优化模型，用于河流水质管理制度。Tsay等[12]应用灰色关系分析对流域水污染进行了探讨。Xia[13]基于灰色预测方法的基础上，以灰色系统理论和正交的扩张模式，提出了一种可能的方法进行预测湖泊的水质。Chang等[14]利用灰色模糊多目标来优化规划水库集水区。

为了解林边溪破堤所产生淤泥淤积深度在空间的分布，笔者在佳冬堤防破堤处取样进行粒径分析，并利用灰关联分析淤泥土壤分层，以分析淤泥覆盖深度。

2 分析方法与理论

2.1 灰关联分析

灰关联分析是灰色系统理论中用以计算离散序列间关联性的测度方法，此种关联性可又分为局部性灰关联分析与整体性灰关联分析两种[14]。笔者依取样顺序所建立关联性为序列间关联性分析，系将于林边溪佳冬乡大同村下方堤岸溃决处所取得的土样，利用各层次序列间的关联性，对各层粒径进行灰关联分析，求出邻近两层灰关联度最小者，即表示两层间之土样级配差异最大，此两层极可能为莫拉克风灾后原土与冲积土之土壤分层，藉由此方法即能推估出淤泥淤积深度。利用灰关联分析的计算步骤如下：

2.1.1 数据处理 由现地取样的土样经筛分析及比重计试验后可得各粒径的通过百分比；但由于比重试验测得的粒径不相同，致使各层粒径的通过百分比无法比较，因此必须将比重试验测得的粒径进行内差及外差使其具有同等级性。因此，数据经初始化后满足可比性，即可进行灰关联度分析。

设有一具顺序关系的序列如式（1）所示。

其中i＝1，2，3，…，m 个土壤层次；k＝1，2，3，…，n种粒径通过百分比；m，n∈N。

2.1.2 计算两层次绝对差值序列 Δi，i＋1（k） 设同一孔土样之上层及下层之粒径分布分别为xi（k）与xi＋1（k），令xi（k）为参考序列，xi＋1（k）为比较序列；取参考序列xi（k）与比较序列xi＋1（k）之差值绝对值，可得于k粒径之通过百分比 Δi，i（k）如式（2）所示。

2.1.3 求最小差值Δmin及最大差值Δmax最小差值及最大差值，其定义为参考序列xi（k）与比较序列xi＋1（k）之绝对差值序列中的最小值及最大值，如式（3）及式（4）所示。其中i为土样之层次，共有m层，与k种粒径通过百分率。

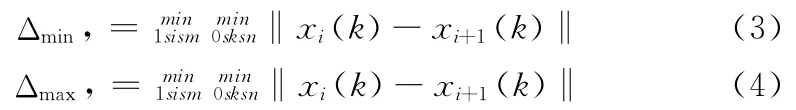
2.1.4 计算灰关联系数ζj，j＋1（k） 灰关联系数ζi，i＋1（k）如式（5）所示：

2.1.5 计算灰关联度 在求得灰关联系数后，取灰关联系数的平均值为灰关联度。灰关联度如式（6）所示。

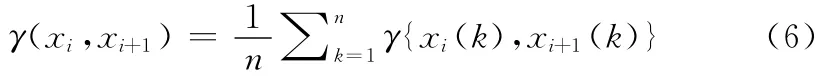
2.2 FLO－2D模式

为检验林边溪溃堤所产生的淤积土层分布趋势与水流流向之一致性，笔者利用FLO－2D模式来仿真破堤所产生的流场分布。FLO－2D为二维淹水数值模式，系由O’Brien等[15]于1988年提出，其数值解法是应用中央有限差分法来求解流体运动方程式，以求得x与y方向之平均流速u及v，并计算流体深度h等。此模式适用于洪水平原管理、都市淹水、工程风险设计、溃坝仿真、不规则形状河道及桥梁涵洞水理演算，可以处理都市水文、漫地流、泥流及土石流等问题。笔者应用FLO－2D模式将林边溪流域以每一网格为100m×100m将仿真区域划分，总计有3 672个网格数，应用以往的降雨事件验证模式的参数后，再针对莫拉克台风单场降雨事件，进行洪水流场模拟。

3 研究区域概述

林边溪流域北隔东港溪与隘寮溪流域，东以中央山脉与太麻里溪流域为界，南接率芒溪流域，西邻台湾海峡，主要支流包含瓦鲁斯溪、大后溪、来社溪、尖刀尾溪、七佳溪、力力溪等，发源于中央山脉之南大武山西南麓（标高2 950m），集水区高低落差大，且流路纵坡相当陡峭，流路短促、溪床陡峻、谷深、向源侵蚀显著，河流中、下游两岸多有河阶地与冲积扇之发育，出口处为林边溪冲积扇；林边溪主流于屏东县林边乡、佳冬乡界注入台湾海峡，主流长41.3km，流域面积为345.2km2，流域概况如图1所示[16]。

本区在地形上属典型台湾幼年期河川特性，向源侵蚀明显、河床纵坡陡峻、河道冲刷与淤积变异量大，河床在汇流口处形成台阶地形，流域的地形高度落差大，地形大致自东向西陡降，高差约3 000m，以位于东侧来义乡地势最陡；标高大部份在1 000m以上占流域面积24.64%，标高在1 000m至100m之间者占流域面积的53.02%，标高在100m以下占流域面积的22.34%，集水区内多为海拔1 000m以下，地势平缓，为典型西部河川[16]。

本区地质主要以中新世地层组成，流域内仅有两条区域性断层，其中一条潮州断层；另一条为未确定位于潮州断层左方，土壤上游山区部分为森林土及石质土，下游为冲积土。气象条件之年平均气温为26.1～28.3℃；以潮洲站为例，年日照时数约为1，568h，月平均日照时数约为131h，平均风速约0.2m／s，年平均雨量约2 115mm[16]。

4 分析与讨论

笔者所分析的资料是2009年8月6日至8月8日莫拉克台风侵台时，造成林边溪佳冬堤防破堤处所产生的淤泥淤积处取得，经现地勘查后选择21个取样点位，位置如图2所示。取样方式为分层取样，每15公分为一层，取样深度为150μm或取至原土层下30μm；因此，每个取样点视现场状况分成6～10层不等，共计取得162个土样。并记录每取样点的坐标位置，以分析其淤积深度的空间分布。土样取得后，经气干再进行粒径分析，分析方法包括筛分析与比重计试验两种方法，由试验结果可得各土样的粒径分布曲线，以此曲线求得各种粒径的通过百分比，以作为灰关联分析初始资料。

图1 林边溪流域概况图[16]

利用式（2）至式（6）的方程式计算各孔土壤取样分层间的灰关联度如表1所列，利用FLO－2D所模拟林边溪破堤时的水流流场与淤积等深线如图3所示。由表1中的各取样土壤分层的最小灰关联度即为淤积土层与原土层分界位置，取两层交界处的深度为溃堤淤泥的淤积深度，而由图3的流场方向可用于解释淤积深度分布的可能原因。经由灰关联分析结果可知，点2处的淤积最深，此区因位于破堤的主要水流方向且因邻近区域排水渠道，于积水退去后，此排水渠道已被淤泥覆盖，推估其原因为破堤初期所沉降的土质为砂质，待降雨缓和后形成区域淹水，而成为细颗粒沉降，但因渠道内下游处受淤积甚浅，积水由区域排水排出时会带动细颗粒向区排方向移动，致使本区的淤积最深。点12亦有与点2相同的淤积机制。而点5，6，7亦位于破堤的主要水流方向，但因此3点位于区域排水东侧，致淤泥随水流流向越过区域排水后方淤积于此区域，故此区域的淤积深度低于点2处。点1处距破堤处最近，但因位于上游处，故其淤积深度低于点2处，但高于其他点位。点8至点11等位于水流下游方向，其淤积深度亦较浅。而淤积最浅的区位为点13处，因此取样区为田区，邻近住户少，由分析结果可知其灰关联度最小者位于30cm处，但依实际取样现况判断，本区的淤积深度应位于90cm处。点20及点21之区位因距离破堤处较远，又因水流需经区域排水后再流至该区域，然由灰关联分析可知其灰关联度最小者位于取样的最底层处，由实际状况分析，该分层可能为长期农作翻田后灌溉所产生的土层接口，而由灰关联度之变化曲线分析，淤积深度应位于45cm处的接口。

由图3的淤泥淤积等深度线与FLO－2D模式仿真的流场方向比对，可得知流场方向与淤泥淤积等势线具一致性，是由高势能区域流至较低势能区域。并由FLO－2D模式仿真的流场型态得知水流与泥砂流是由破堤口涌入向两旁呈扇形、锥形堆积扩散，而由图中的土壤淤积等势线可知洪水在流经农舍及住家地区时泥砂淤积有更显著的现象，而在其分布情形上，可知在经过区域性排水系统之地区分布较为密集，淤积深度变化较大。由此可见，水流与泥砂流的流向亦会受到水工构造物及建筑物影响。

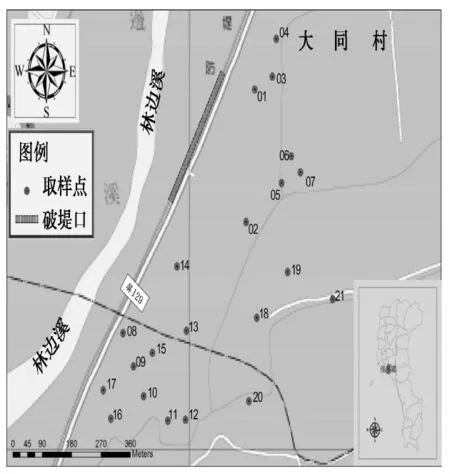
图2 佳冬堤防溃堤处取样点位分布图

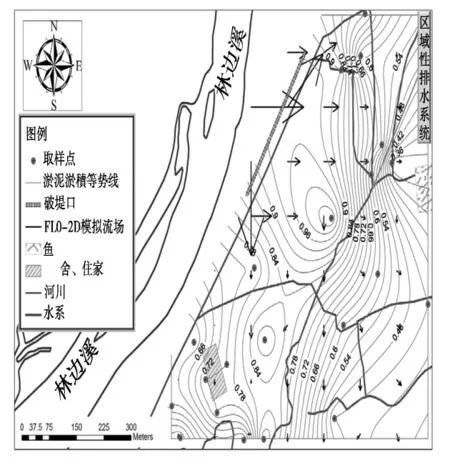
图3 FLO－2D淹水模拟流场方向与淤泥淤积等深线比较图

表1 计算得之灰关联度与推估出的淤积深度值

5 结 论

应用灰关联分析2009年8月7日莫拉克风灾造成屏东县林边溪破堤处的淤泥淤积深度分布，并配合FLO－2D的淹水模拟所得知的流场方向来评估淤泥淤积深度分布的机制，由分析结果可得知在破堤的主要水流方向且因邻近区域排水渠道的区域，因区域排水系统于破堤初期所沉降的土质为砂质，待降雨缓和后形成区域淹水，而成为细颗粒沉降，但因渠道内下游处受淤积甚浅，积水由区域排水排出时会带动细颗粒向区排方向移动，致使此区的淤拟淤积深度最深。另随破堤时水流所夹带淤泥的淤积深度及淤积土壤颗粒分布型态，并以流场方向的验证，可分析林边溪堤岸破堤时的水流流向，由此可作为减灾应变的依据。

[1]国家灾害科技中心.莫拉克台风灾区勘灾行动计划期末报告－屏东县与台东县[M].国立屏东科技大学，2010.

[2]DENG JL.Control problems of grey system [J].System ＆Control Letters，1982，1（5）：288－294.

[3]叶一隆，林信宏，林国华，等.应用灰关联分析休耕水田蓄水区位评估[J].台湾水利，2010，58（1）：46－54.YEH YILUNG，LIN SHINHUNG，LIN KUOHUA，CHEN TINGCHIEN.2010， Evaluation of storage water sites in fallow paddy fields using grey relational analysis[J].Taiwan Water Conservancy，2010，58（1）：46－54.

[4]叶一隆.日降雨型态重现之灰关联分析[J].台湾水利，2003，51（4）：89－97.YEH YILUNG.Recurrence analysis of daily rainfall pattern using grey correlation method[J].Taiwan Water Conservancy，2003，51（4）：89－97.

[5]黄皇嘉，温志超，谢孟益.降雨量大小对土壤入渗机制之影响[J].农业工程学报，2005，51（1）：34－45.HUANG HUANGJIA，WEN JETCHAU，HSIEH MENGI.The infiltrating mechanism of soils for scales of precipitation[J].Journal of Chinese Agricultural Engineering，2005，51（1）：34－45.

[6]WONG H，HU B Q，IP WC，et al.Change－point analysis of hydrological time series using grey relational method [J].Journal of Hydrology，2006，324：323－338.

[7]TRIVEDI H V，SINGH J K.Application of grey system theory in the development of a runoff prediction model，Biosystems Engineering，2005，92（4）：521－526.

[8]YU P S，CHEN C J，CHEN S J.Application of grey and fuzzy methods for rainfall forecasting [J].Journal of Hydrologic Engineering，2000，5（4）：339－345.

[9]IP W C，HU B Q，WONG H，et al.2009，Applications of grey relational method to river environment quality evaluation in China[J].Journal of Hydrology，2009，379：284－290.

[10]Yeh Y L，Chen T C.Application of grey correlation analysis for evaluating artificial lake site in Pingtung Plain，Taiwan [J].Canadian Journal of Civil Engineering，2004，31（1）：56－64.

[11]MUJUMDAR P P.Grey fuzzy optimization model for water quality management of a river system [J].Advances in Water Resources，2006，29：1088－1105.

[12]TSAY J S，LO J J，WU J H.Application of grey relational analysis to river water pollution [J].The Journal of Grey System，2000，12（4）：391－398.

[13]XIA J.A grey system method applied to forecasting of lake water quality[J].The Journal of Grey System，1990，2（2）：257－265.

[14]CHANG N B，WEN C G，CHEN Y L，et al.Optimal planning of the reservoir watershed by grey fuzzy multi－objective programming（I）：Theory [J].Water Research，1996，30（10）：2329－2334.

[15]O’BRIEN J S，JULIEN P Y，FULLTERTON W T.Two dimensional water flood and mudflow simulation[J].Journal of Hydraulic Engineering，1993，119（2）：244－259.

[16]经济部水利署水利规划试验所.易淹水地区水患治理计划－屏东县管河川林边溪水系治理规划总报告[M].经济部水利署，2008.