基于最小二乘法的LabVIEW拟合桥梁挠曲线研究

朱定国

(上海市水利工程设计研究院，上海市 200061)

0 引言

桥梁在外荷载作用下的变形、结构材料的变异等都能够通过挠度的变化表现出来，挠度是桥梁健康状态最直观、有效的参数之一，所以桥梁挠度及线形测量的精度、准确性及测试效率一直是业界所关注的热点问题。

目前桥梁挠度测量一般采用如下方法[1-5]：（1）利用百分表和千分表测量挠度。此法固定底座安装不易，数据采集困难，效率较低。（2）GPS挠度观测。此法系统价格昂贵，测量精度低，测点少，受干扰大。（3）利用水准仪进行挠度观测。此法误差因素多，测量速度慢耗时长，仪器操作复杂，而且需要封桥，时间长，效率较低。（4）用加速度计测量桥梁加速度，通过两次积分得挠度。此法难以选择合适的加速度计，存在较大的幅值误差，安装布线困难，难以进行实时监测。（5）采用倾角仪测量挠度。此法精度不够，反算结构挠度较慢，使用范围较窄。（6）利用连通管方法测量挠度。此法测量环境有限制，液面易挥发和污染。

综上所述，我们可以看到桥梁挠度测量的方法有很多，但是每种方法都有其缺点，要么操作复杂耗时长，要么精度效率低，要么价格昂贵，所以为了桥梁健康监测与检测的需要，有必要设计一种基于光纤光栅传感器的挠度测量方法，达到实时长期监测桥梁挠曲线的目的。本文介绍了基于平均曲率采用最小二乘法分跨拟合桥梁挠曲线测试方法的原理、算法，推导了相应的公式，介绍并应用LabVIEW编写了相应的专业软件，并通过数值模拟验证了其具有很高的精度。可以为同类桥梁的分析研究、监测评估提供参考依据。

1 桥梁的应变、曲率和挠度的关系

曲率是度量梁弯曲变形的程度，用k表示。由材料力学的知识，曲率等于曲率半径的倒数即：

由材料力学还知某点线应变：

其中y为该点到中性轴的距离。

由上面两式可得：

对于同一横截面曲率是常数，由式（3）可知曲率k与线应变ε成线性关系，知道某点的线应变ε以及该点到中性轴的距离y就能得到该点的曲率，进而由很多个点的曲率可以得到曲率函数，且曲率函数积分两次后就是挠曲线，这样就可以利用曲率建立起应变与挠度的关系。

2 平均曲率

由式（3）可知要想求出传感器所在截面的曲率必需先测出传感器到中性轴的距离y。而这一距离是很难精确测量的，所以本文拟采用平均曲率的方法加以解决。即将两个FBG传感器安装在与中性轴平行的位置。下面给出了3种情况：图1(a)为FBG传感器都位于梁的中性轴下面，图1(b)为分别位于上下方，图1(c)为都位于上方。

如图1(a)所示，测点1、2的单元曲率为：

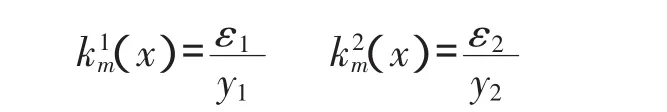
由上两式可得此单元的平均曲率为：

如图1（b）所示，测点1、2的单元曲率为：

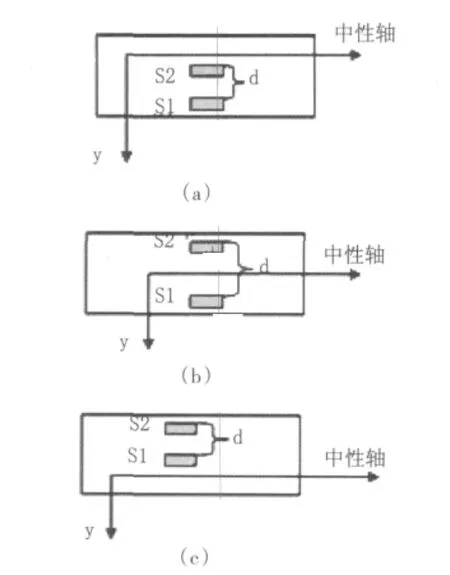
图1 单元中FBG安装示意图

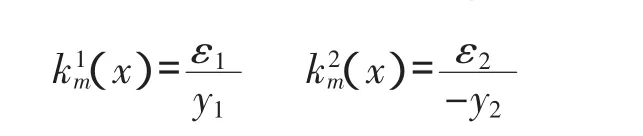
由上两式可得此单元的平均曲率为：

如图1（c）所示，测点1、2的单元曲率为：

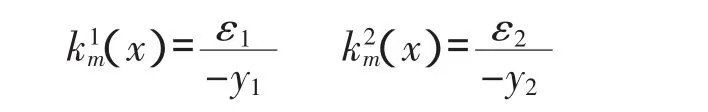
由上两式可得此单元的平均曲率为：

由式（4）、（5）、（6）可知单元的平均曲率与梁的中性轴的位置无关，只要将两个传感器平行于中性轴安装，此单元的平均曲率可统一表示为：

3 最小二乘法曲线拟合原理

最常见的最小二乘法拟合曲线模式是多项式：

由式(7)可知，通过将两个FBG传感器平行于中性轴安装就可以测得此单元的曲率ki，然后沿桥梁的纵向安装若干组这样的传感器就可以得到一组测量数据（xi，ki），然后通过最小二乘法就可以拟合出曲率曲线了。

4 分跨拟合挠曲线原理

假设待测桥梁有n跨，基函数取为：

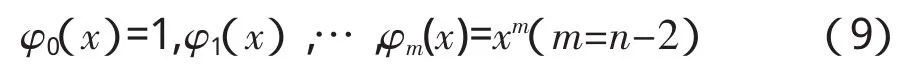
则第k（1≤k≤n）跨的曲率函数为：

k跨内各单元曲率由式（7）得到。

将式（9）积分两次即可得到挠曲线：

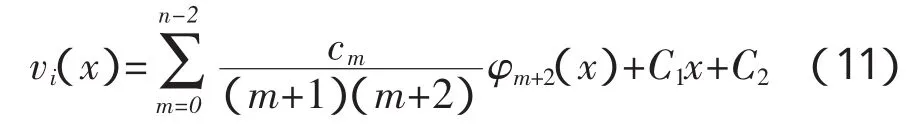
C1、C2为积分常数，可由左右两端支座沉降求得，如左端沉降为Δ左，右端沉降为Δ右，设跨长为l，则：

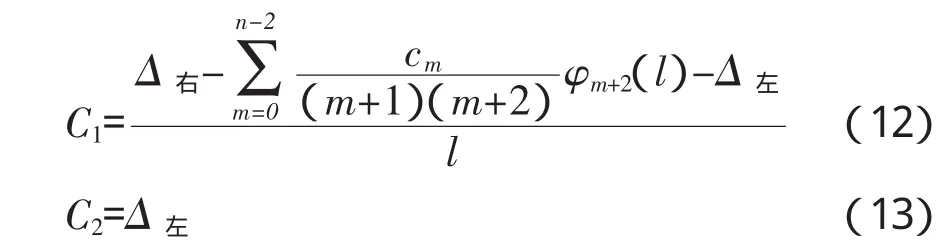
求得每跨挠曲线后，叠加即可得到整个待测桥梁的挠曲线：

5 数值模拟验证

本文采用LabVIEW软件作为工具编写了根据测得的曲率用最小二乘法拟合桥梁挠曲线的软件。为了证明此方法的可行性与准确性，这里对简支梁在多种不同荷载作用下的挠曲线进行了数值模拟。模拟中根据各截面处的平均曲率，运用根据最小二乘法所编写的LabVIEW程序拟合了挠曲线，并且将拟合值与理论值进行了比较，得到了相对误差。

通过模拟发现精度对跨度不敏感，但是精度对传感器安装截面个数较敏感，为了达到良好的精度，截面个数取多为宜，本次模拟假设简支梁跨度为50 m，每隔5 m安装一组传感器，即以9个截面安装传感器。

5.1 受跨中集中荷载

跨度l=50 m的简支梁受跨中集中荷载作用，P=300 kN，截面特性 EI=3.5×1010N·m2，如图 2所示：

图2 简支梁受跨中集中荷载

根据理论计算，图2所示结构挠曲线和曲率表达式为：

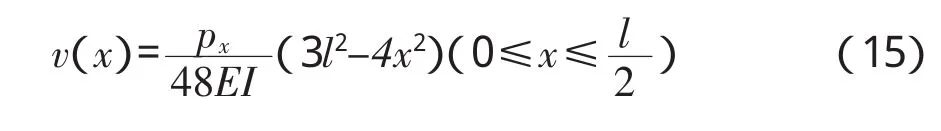
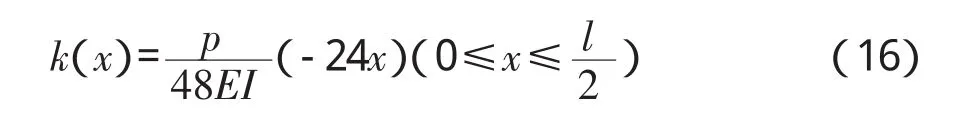
由式(16)求得结构的理论曲率值，然后根据LabVIEW编写的桥梁挠曲线拟合软件拟合出结构的挠曲线（如图3），图中还列出了拟合值与式(15)计算的理论值的相对误差。

图3 跨中集中荷载拟合挠曲线及与理论挠度值的比较

从图3中可以看出本文方法拟合得到的挠度值与理论挠度值误差很小，最大误差为1.21667%，能满足工程需要。

5.2 受3/4跨集中荷载

跨度l=50m的简支梁受3/4跨集中荷载作用，P=300 kN，EI=3.5×1010N·m2截面特性，如图4所示：

图4 简支梁受3/4跨集中荷载

根据理论计算，图4所示结构挠曲线和曲率表达式为：

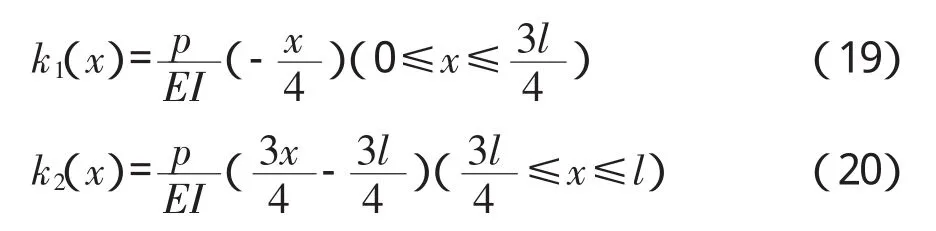
由式(19)、(20)求得结构的理论曲率值，然后根据LabVIEW编写的桥梁挠曲线拟合软件拟合出结构的挠曲线（如图5），图中还列出了拟合值与式(17)、(18)计算的理论值的相对误差。

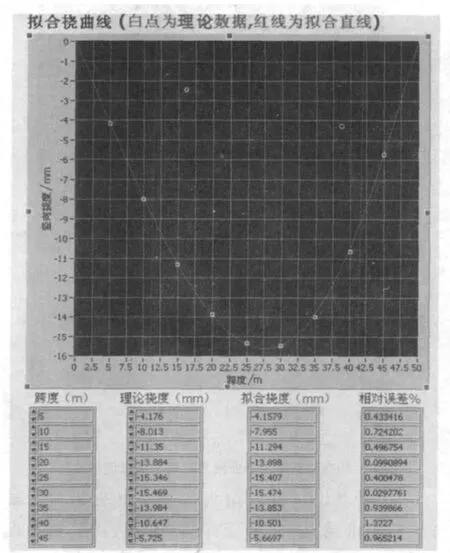
图5 3/4跨集中荷载拟合挠曲线及与理论挠度值的比较

从图5中可以看出本文方法拟合得到的挠度值与理论挠度值误差很小，最大误差为1.372 7%，能满足工程需要。

5.3 受均布荷载

跨度l=50m的简支梁受均布荷载作用，q=10 kN，截面特性EI=3.5×1010N·m2，如图 6所示。

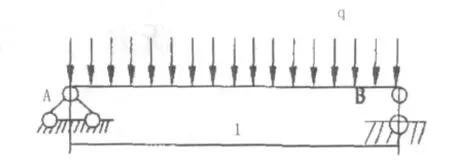
图6 简支梁受均布荷载

根据理论计算，图6所示结构挠曲线和曲率表达式为：

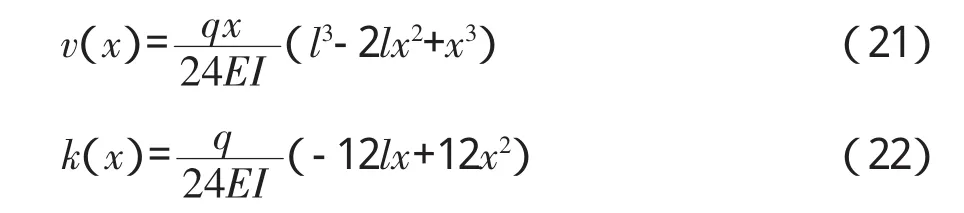
由式（22）求得结构的理论曲率值，然后根据LabVIEW编写的桥梁挠曲线拟合软件拟合出结构的挠曲线（如图7），图7中还列出了拟合值与式（21）计算的理论值的相对误差。

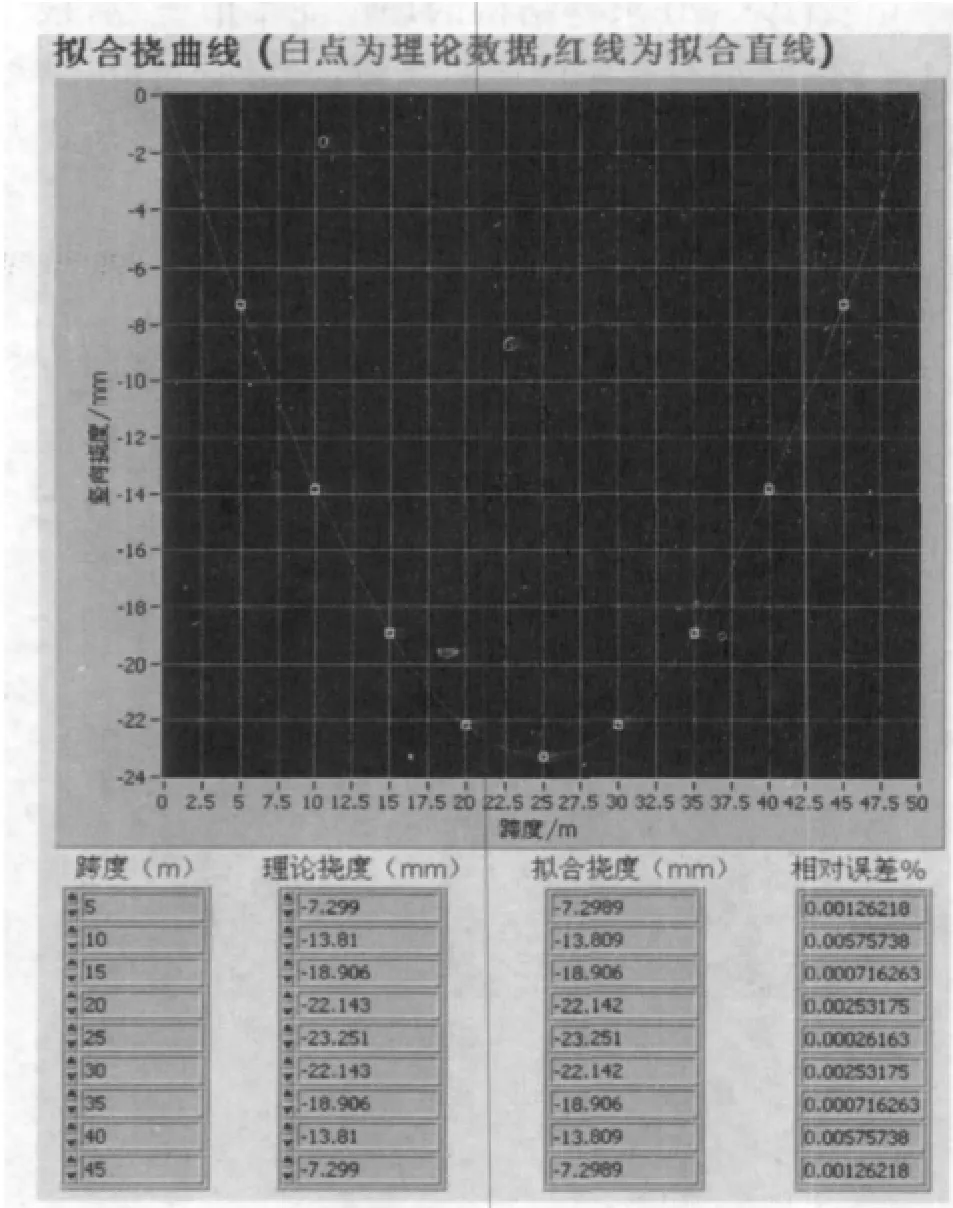
图7 均布荷载拟合挠曲线及与理论挠度值的比较

从图7中可以看出当所受荷载为均布荷载时，精度非常高，几乎没有误差（如图7），最大误差仅为0.005 757%。我们知道，实际桥梁主要受车辆荷载，经桥面板分配后，主要承受的就是均布荷载或三角荷载，这样采用此方法来拟合桥梁挠曲线就具有更好的效果。

6 结论

目前已有的基于光纤Bragg光栅的各种传感器基本上都是直接或间接地利用应变或温度改变光栅中心波长，达到测试被测物理量的目的。FBG的测试基本物理量是应变，无法直接测试挠度。而挠度又是桥梁健康状态最直观、有效的表现形式之一。本文基于该现象，采用最小二乘法由截面的平均曲率分跨拟合桥梁的挠曲线，达到由FBG测试桥梁挠曲线的目的。并通过使用LabVIEW软件编制由曲率拟合挠曲线的专业程序，可以得到任意荷载作用、跨长、支座沉降情况下的挠曲线方程。

通过简支梁受跨中集中荷载、3/4跨集中荷载以及均布荷载3种工况，用所编制的程序拟合得到的挠度值与理论挠度值进行比较。比较发现用最小二乘法拟合桥梁挠曲线的方法具有很高的精度。比较3种结果，发现程序精度与荷载的作用方式有关，当所受荷载为均布荷载时，精度非常高，几乎没有误差（如图7）。我们知道，实际桥梁主要受车辆荷载，经桥面板分配后，主要承受的就是均布荷载或三角荷载，这样采用此方法来拟合桥梁挠曲线就具有更好的效果，此方法用于实时监测桥梁的挠度变化曲线是可行的。

[1]汪正兴,王 波,钟继卫,朱世峰.基于液一气耦合压差原理的桥梁挠度测量系统研究[J].桥梁建设,2009（S2）：78-83.

[2]胡伍生.水准测量法观测桥梁挠度的应用 [J].华东公路,1996（2）：72-74.

[3]袁向荣.桥梁动挠度计算的加速度积分方法[J].广州大学学报(自然科学版),2007,6（1）：75-78.

[4]叶贵如,周玉龙.倾角仪在大跨度桥梁挠度检测中的应用[J].公路交通科技,2009,26（l1）：103-107.

[5]曾威,于德介,胡柏学,刘克明,郭建文.基于连通管原理的桥梁挠度自动监测系统[J].湖南大学学报(自然科学版),2007,34（7）：44-47.