具有宽负载范围的新型Boost功率因数校正器
于海坤 许建平 张 斐 王金平
(西南交通大学电气工程学院 成都 610031)
1 引言
功率因数校正技术可有效减少网侧电流谐波含量,提高电源功率因数,是电网供用电设备不可或缺的重要组成部分。Boost变换器因其拓扑结构简单、变换效率高、控制策略易实现等优点,被广泛用作PFC电路[1]。
Boost变换器的工作模式分为不连续导电模式(Discontinuous Conduction Mode, DCM)和连续导电模式(Continuous Conduction Mode, CCM)两种。DCM Boost PFC变换器的平均输入电流自动跟踪输入电压,不需要专门的电流控制回路即可实现功率因数校正。但是,由于DCM Boost PFC变换器的电感电流在每个开关周期内有一段保持为零,若变换器传递更多能量给负载,只能大幅提高电感电流峰值,导致开关管电流应力大以及EMI较为严重,因而 DCM Boost PFC变换器仅限于小功率场合的应用(一般小于250W)[2-4]。CCM Boost PFC变换器可以有效减少开关管的电流应力,在中、大功率场合得到了广泛的应用。但在负载较轻时,CCM Boost PFC变换器的电感电流在输入电压过零点附近出现断续现象,开关变换器工作在混合工作模式(Mixed Conduction Mode, MCM),此时变换器的动态特性急剧变化,CCM模式的采样和控制策略将导致变换器输入电流严重失真[1-4]。因此,DCM Boost PFC和CCM Boost PFC变换器均只适用于特定的负载范围。
当负载范围变化较宽时,根据负载大小在CCM和 DCM两种工作模式之间进行选择性切换是一种有效的解决方案。文献[2]在传统Boost变换器中增加额外的滤波电感电容,负载功率大于阈值时增加升压电感量以确保电感电流工作于 CCM模式,反之则减小升压电感量使其工作于 DCM模式。文献[3]提出采用两个开关频率的控制思想,当负载减小时大幅降低开关频率达到电感电流断续的目的,从而避免系统工作在 MCM 模式。上述方案存在EMI滤波器参数设计难度大、控制算法复杂的缺点。文献[4]针对MCM现象,在传统CCM双环控制的基础上,通过增加数字采样校正和占空比前馈控制环以改善输入电流波形,但该控制方案对数字控制芯片的处理速度要求很高。
伪连续导电模式(Pseudo Continuous Conduction Mode, PCCM)是一种介于DCM与CCM之间的第三种工作模式。在一个开关周期内,它存在与DCM类似的三个工作状态,但其第三个工作状态的电感电流不为零。相对于 DCM Boost变换器,PCCM Boost变换器具有电感电流纹波小、负载能力强的优点;相对于CCM Boost变换器,PCCM Boost变换器具有与 DCM Boost变换器类似的功率级小信号传递函数,不存在CCM Boost变换器的右半平面(Right Half Plane, RHP)零点,在DC-DC变换器中具有理想的动态性能[5-7]。
本文提出了工作于PCCM模式的Boost PFC变换器,分析了PCCM Boost PFC变换器的工作原理,根据其特有的两个控制自由度,建立了两个并行的控制环路,在此基础上,针对负载变化范围较宽时具备高功率因数的控制目标,对控制系统进行了详细的设计。最后通过 PCCM Boost PFC变换器与CCM Boost PFC变换器的对比实验验证了控制该方案的有效性。
2 PCCM Boost PFC变换器
2.1 PCCM Boost变换器工作原理
图1a为PCCM Boost变换器电路,其主要工作波形如图1b所示。与常规Boost变换器相比,PCCM Boost变换器增加了与电感并联的辅助开关和二极管。PCCM Boost变换器在一个开关周期内存在三个工作状态,分别如图2a~图 2c所示。在 d1Ts时间段,主开关S1导通,电感电流IL以Vin/L的斜率上升到峰值 Ip;d2Ts时间段,二极管 VD1导通,IL以 (Vo-Vin)/L的斜率下降到谷值 Idc;d3Ts时间段(也称惯性阶段[5]),辅助开关 S2和二极管 VD2导通,电感两端短路,忽略电感寄生电阻时,IL保持不变。

图1 PCCM Boost变换器及其主要波形Fig.1 PCCM Boost converter and its main waveforms
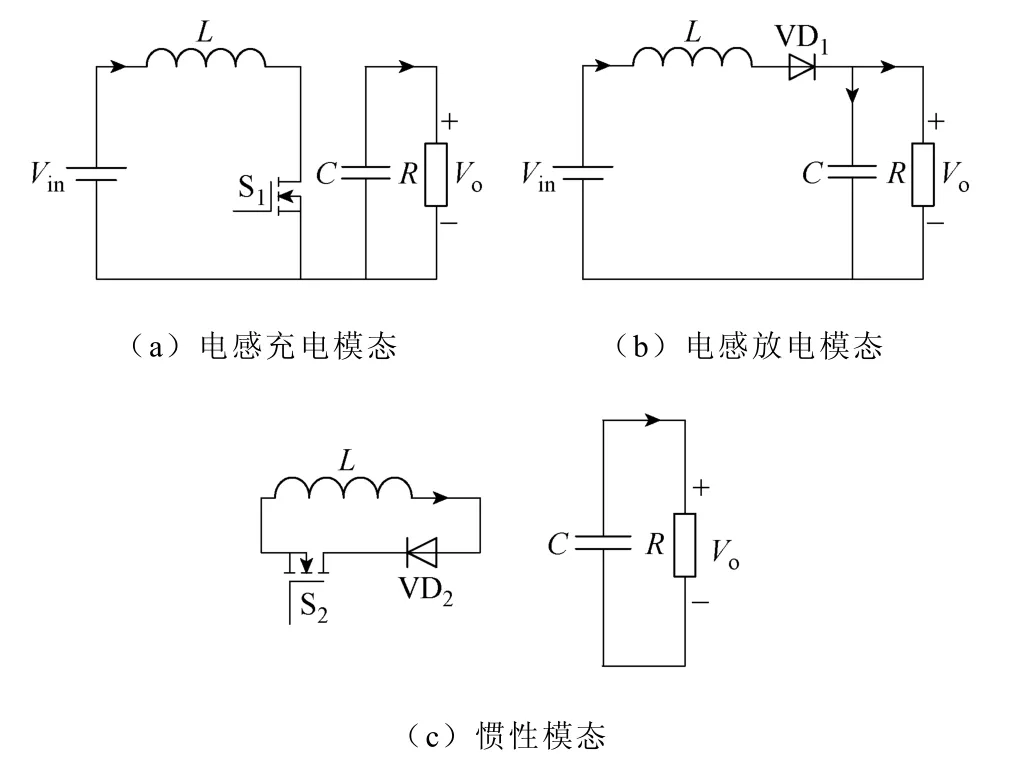
图2 PCCM Boost变换器等效电路Fig.2 The equivalent circuit of PCCM Boost converter
由图1b可知,PCCM Boost变换器的电感电流波形与DCM Boost变换器的电感电流波形相似,所不同的是,PCCM Boost变换器的电感电流IL在惯性阶段不为零,因此,在相同输出功率的情况下,PCCM Boost变换器两个开关管的电流应力均远小于 DCM Boost变换器开关管的电流应力。相对于CCM Boost变换器,PCCM Boost变换器消除了二极管VD1的反向恢复损耗,但在惯性阶段辅助开关S2和二极管VD2存在额外的导通损耗(当输入电压较高时,可忽略不计[6])。
利用开关变换器的时间平均等效电路分析方法[8],可得PCCM Boost变换器的直流大信号模型为
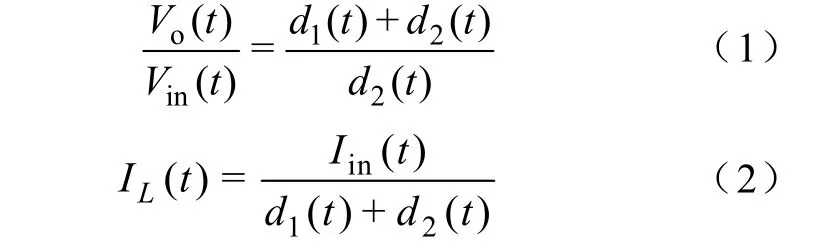
由式(1)、式(2)可知,通过改变 d1(t)/d2(t)的比值,可以实现输出电压的调节。PCCM 工作时d1(t)+d2(t)<1,变换器的平均电感电流大于平均输入电流。
2.2 PCCM Boost PFC变换器控制策略研究
PFC变换器需要在实现输出直流电压控制的同时,使输入电流与输入正弦电压同频率同相位,因此,需要两个控制量。而PCCM Boost变换器正好存在两个控制自由度 d1和 d3,非常符合 PFC的要求。文献[7]通过建立系统的控制到输出的传递函数的矩阵方程,将变换器等效为二维可变的受控系统,并用相对增益阵列法得出 Vo与主开关控制信号 d1相关,IL与辅助开关控制信号d3相关的组合控制方式。
如图3所示为本文设计的PCCM Boost PFC变换器数字控制方案,它有电压环和电流环两个控制环路。输出电压与参考电压的误差信号经电压 PI环后控制主开关S1;采用谷值电流跟踪算法控制辅助开关S2,当电感电流IL下降到参考正弦点时使其导通,保证IL的谷值呈正弦变化。当PCCM Boost PFC变换器工作于稳态时,主开关占空比 d1(t) 保持恒定,而d2(t)、d3(t) 按正弦规律变化。
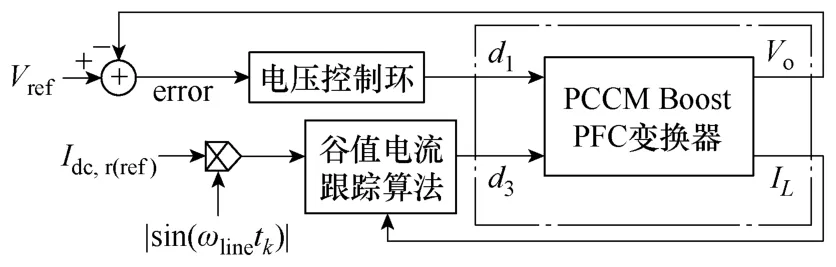
图3 控制系统框图Fig.3 Block diagram of control system
在本文中,下标r表示交流变量的有效值,Vin,r与 Iin,r分别表示输入电压和输入电流的有效值,Vo表示稳态直流输出电压,则式(1)和式(2)可转换为
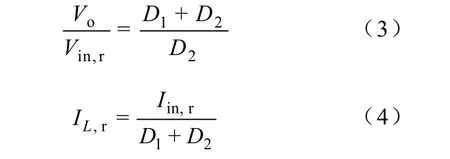
式中 D1——占空比d1(t) 的直流工作点;
D2——d2(t) 的有效值工作点。
当忽略变换器损耗时,根据功率平衡原理,可得
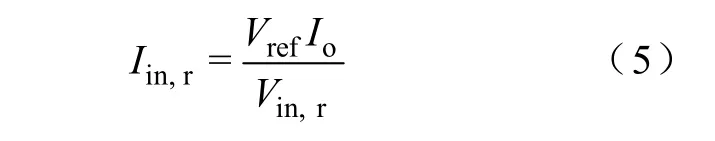
由上面的分析可知,PCCM Boost变换器的平均电感电流大于平均输入电流,则由式(5)可知,以负载电流为参考量,实时调整电感电流幅值,可得
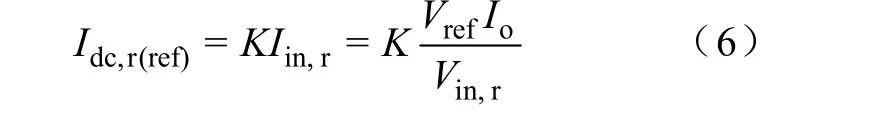
式中,K>1可保证Boost变换器工作于PCCM模式。当忽略电感电流纹波时,联立式(4)、式(6)得
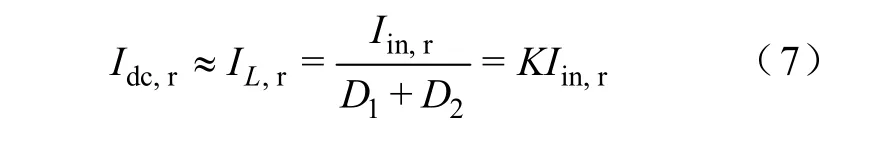
将D1+D2+ D3=1代入式(3)和式(7),整理得
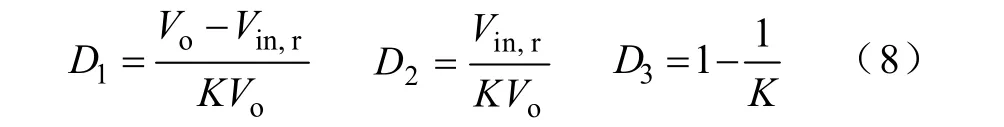
由式(8)可知,系统各个控制信号的稳态工作点与K有关。当K值较低时,惯性阶段时间较短,通过减小惯性阶段时间,可以提高PCCM Boost变换器的效率。因此,在保证 Boost变换器工作于PCCM模式的前提下,选择较小的K值,可以最大限度地降低辅助开关 S2和二极管 VD2引起的额外导通损耗。
值得注意的是,由于输入电压呈正弦波动,PFC变换器输出电流含有偶次谐波量。若直接采样负载电流作为电流控制环路的参考电流,将影响参考电流的正弦度。为了解决这一问题,可以采用纹波补偿法、采样保持法、交替边缘采样等算法[9]。输入电压过零点采样保持法实现简单可靠,可保证参考电流幅值不受谐波影响,但会降低参考电流的响应速度。在本文设计的PCCM Boost PFC变换器中,参考电流的作用是保证系统的稳态性能,而其动态响应速度主要由电压环决定,因此可以采用如图 4所示采样保持法设计参考电流幅值。
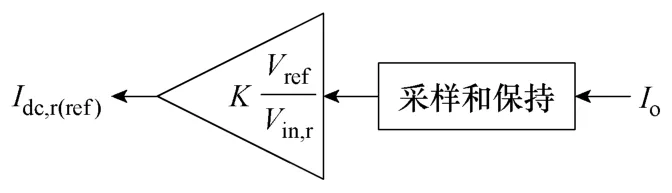
图4 参考电流幅值设计方案Fig.4 The design scheme of reference current amplitude
3 PCCM Boost PFC变换器控制系统设计
3.1 PCCM Boost PFC变换器电流环设计
如图5所示为数字电感电流谷值控制示意图,图中实线为实际电感电流谷值的正弦曲线,虚线为参考电流曲线。由于变换器的开关频率远大于电网频率,因此,在每一个开关周期内,可认为输入电压和输出电压恒定不变。
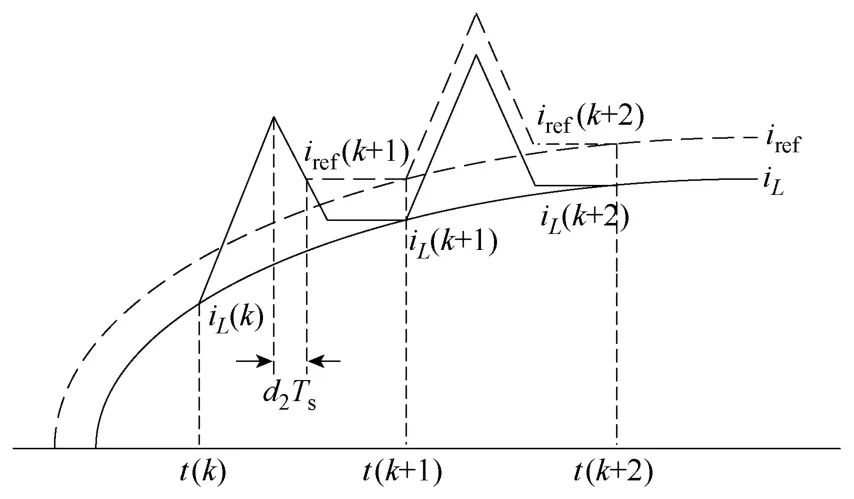
图5 数字电流谷值控制示意图Fig.5 The waveforms of digital valley current control strategy
根据电感电流工作过程可得
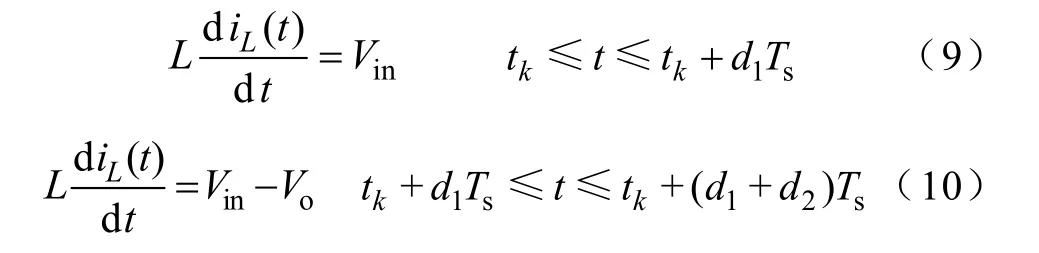
由式(9)和式(10)可得电感电流在第 k与k+1个开关周期起始点的离散表达式如下:
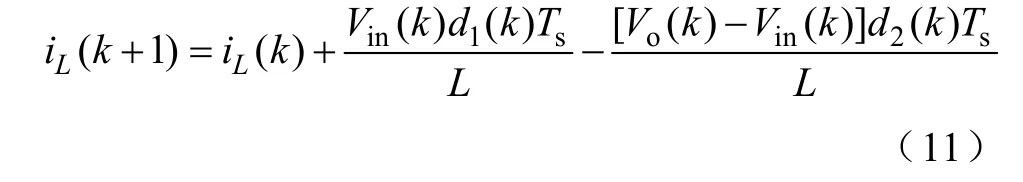
为使第k+1个周期起始时刻电感电流谷值跟踪参考电流,输出电压跟踪参考电压,可得
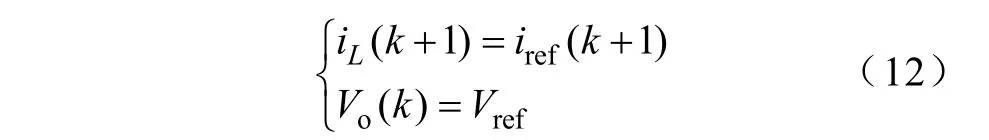
代入式(11)可得
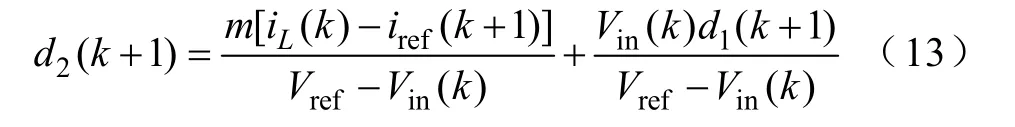
式中,m=L/Ts,参考电流iref(k+1) 由参考电流幅值与当前输入电压相位相乘后得到,Vin(k) 和iL(k) 直接采样得到,d1(k+1) 由电压环计算得知。
3.2 PCCM Boost PFC变换器电压环设计
对于PCCM Boost PFC变换器,将变换器大信号模型中各交流变化量用其有效值替代,交流变化等效为有效值工作点的纹波,则PCCM Boost PFC变换器功率级的动态小信号模型可近似为对应的PCCM Boost 变换器的动态小信号模型[10]。根据PCCM Boost变换器的状态空间方程[7],可得PCCM Boost PFC变换器控制到输出的交流小信号传递函数为
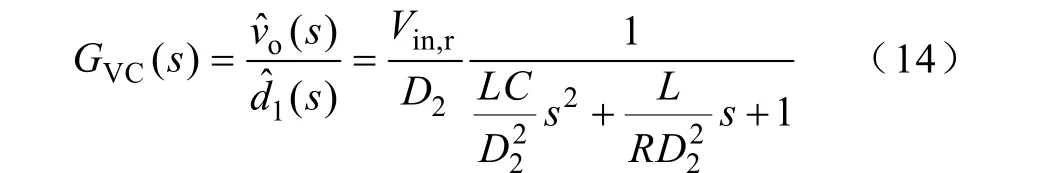
式中,D2为式(8)计算得到的d2(t)有效值。与CCM Boost变换器不同的是,式(14)所描述的PCCM Boost变换器的传递函数为简单的二阶系统,分子项不存在动态移动的RHP零点,从而使电压环的补偿设计更加简单且精确。
PCCM Boost PFC变换器的电压PI环可设计为

设置补偿零点频率fzv远小于二倍网频,则电压环带宽主要由KP决定。额定负载情况下环路在截止频率fcv处的增益为1,因此可由下式计算补偿参数:
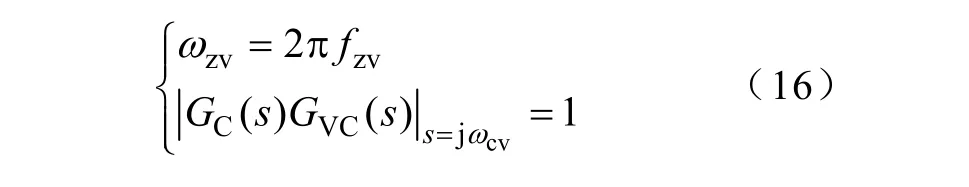
传统平均电流控制 CCM Boost PFC变换器中参考电流幅值由电压环输出信号决定,为避免将输出电压的二次谐波分量引入电流环,需要使电压环带宽低于二倍工频的1/4(一般为10~20Hz)[3]。本文提出的PCCM Boost PFC变换器中,其参考电流信号由负载电流采样保持控制,不受电压谐波量影响,但电压环带宽的提高会使主开关的占空比含有谐波量,即电感电流峰值波动。因此,本文在设计电压环补偿器时取零点频率 fzv=1Hz,截止频率fcv=20Hz。
4 PCCM Boost PFC变换器实验研究
基于以上分析,本文以 TMS320F2812为控制核心,分别对PCCM和CCM Boost PFC变换器进行了实验研究。PCCM Boost PFC变换器中主开关管采用后缘调制,辅助开关管采用前缘调制。实验电路参数如下:负载功率范围Po=70~400W,输入电压 Vin,r=110V,输出电压 Vo=200V,电容C=470μF,电网频率 fline=50Hz,开关频率 fs=50kHz,PCCM 模式的电感 L=200μH,CCM 模式的电感L=1mH。实验采用TDS3034B数字示波器,通过对波形做快速傅里叶分析以进行PF值计算。
为了验证宽负载范围PFC变换器的性能,图6和图7分别给出了最大负载功率(400W)和最小负载功率(70W)时PCCM与CCM Boost PFC变换器的电感电流、输入电流和输入电压波形。当负载功率为400W时,PCCM与CCM Boost PFC变换器的输入电流波形均有较高的正弦度,PCCM Boost PFC变换器的电感电流应力为7.5A,仅比CCM大2.5A,而 DCM Boost PFC变换器在同样负载功率下的电流应力达到 14A[11],验证了 PCCM 与 CCM Boost PFC变换器具有较大的负载能力。当负载功率为70W时,PCCM Boost PFC变换器具有很好的PFC控制性能,而CCM Boost PFC变换器的电感电流出现了MCM现象,导致输入电流发生畸变。

图6 负载功率为400W时变换器输入电压、电感电流和输入电流波形Fig.6 The waveforms of input voltage, inductive current and input current with 400W load
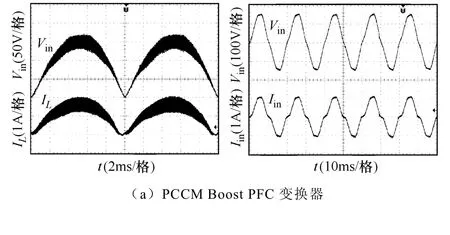
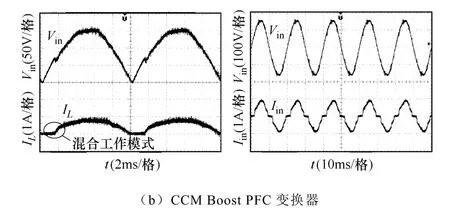
图7 负载功率为70W时变换器输入电压、电感电流和输入电流波形Fig.7 The waveforms of input voltage, inductive current and input current with 70W load
下表为PCCM和CCM Boost PFC变换器在不同负载功率时的输入电流总谐波失真度(THD)和功率因数。由上面的分析可知,PCCM Boost PFC变换器通过实时地调整参考谷值电流与输入电流成固定比例,可保证系统各个控制信号具有稳定的工作点,进而具备稳定的PFC性能。表中的数据表明,在整个负载功率范围内PCCM Boost PFC变换器的PF值均保持在0.975以上且变化不大,与理论分析一致;而CCM Boost PFC变换器的功率因数随负载功率的降低而减小。
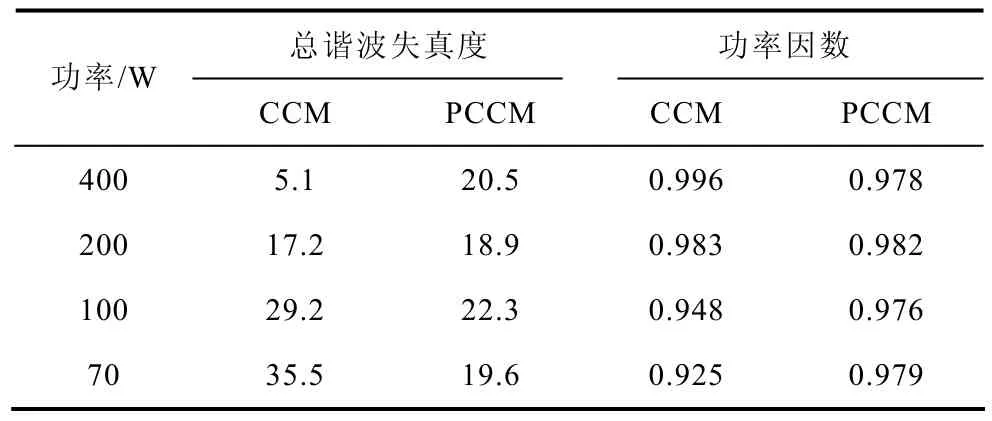
表 PCCM与CCM变换器总谐波失真度和功率因数随功率变化结果Tab.THD and power factor varying with power of PCCM and CCM converter
5 结论
本文针对DCM和CCM Boost PFC变换器负载功率应用范围受限的问题,提出了一种工作于PCCM模式的Boost PFC变换器。详细分析了其工作原理,并设计了相应的数字控制策略。通过PCCM和CCM Boost PFC变换器的对比实验,结果验证了PCCM Boost PFC变换器在宽范围输出功率内具有更好的PFC性能。该电路拓扑同样适合应用于其他类型的PFC变换器,使其能适合功率范围较大的应用场合。
[1]Sebastian J, Cobos J A, Lopera J M, et al.The determination of the boundaries between continuous and discontinuous conduction modes in PWM DC-to-DC converters used as power factor preregulators[J].IEEE Transactions on Power Electronics, 1995, 10(2): 574-582.
[2]Tripathi R K, Das S P, Dubey G K.Mixed-mode operation of boost switch mode rectifier for wide range of load variations[J].IEEE Transactions on Power Electronics, 2002, 17(6): 999-1009.
[3]Rajesh Ghosh, Narayanan G.A single-phase boost rectifier system for wide range of load variations [J].IEEE Transactions on Power Electronics,2007,22(2):470-479.
[4]Gusseme K D, Van de Sype D M, Van den Bossche A P, et al.Digitally controlled boost power factor correction converters operating in both continuous and discontinuous conduction mode[J]. IEEE Transactions on Industrial Electronics, 2005, 52(1):88-97.
[5]Ma Dongsheng, Ki Wing Hung.Fast transient PCCM switching converter with freewheel switching control[J].IEEE Transactions on Circuits and Systems,2007,54(9): 2194-2197.
[6]Kanakasabai Viswanathan,Ramesh Oruganti,Dipti Srinivasan.A novel tri-state boost converter with fast dynamics[J].IEEE Transactions on Power Electronics,2002, 17(5): 677-683.
[7]Kanakasabai Viswanathan,Ramesh Oruganti,Dipti Srinivasan.Dual mode control of tri-state boost converter for improved performance[J].IEEE Transactions on Power Electronics, 2005, 20(4):790-797.
[8]Xu Jianping.Modelling of switching DC-DC converters by timeaveraging equivalent circuit approach[J].International Journal of Electronics,1993:477-488.
[9]Spiazzi G, Mattavelli P, Rossetto L.Methods to improve dynamic response of power factor preregulators: An overview[C].Proceedings of the European Power Electronics Conference, 1995:754-759.
[10]Huliehel F A, Lee F C, Cho B H.Small signal modeling of the single phase boost high power factor converter with constant frequency control[C].Proceedings of the Power Electronics Specialists Conference, 1992: 475-482.
[11]Zhen Z Ye,Milan M Jovanovic.Implementation and performance evaluation of DSP based control for constant frequency discontinuous conduction mode Boost PFC front end[J].IEEE Transactions on Industrial Electronics, 2005, 52(1): 98-107.
[12]马皓,郎芸萍.一种关于单相Boost功率因数校正器数字控制的改进算法[J].电工技术学报,2006,21(2): 83-87.Ma Hao,Lang Yunping.An improved algorithm for DSP implementation of Boost PFC converter[J].Transactions of China Electrotechnical Society, 2006,21(2): 83-87.
[13]Chen Jingquan, Prodic A, Erickson R W, et al.Predictive digital current programmed control[J].IEEE Transactions on Power Electronics, 2003, 18(1):411-419.

