基于细菌觅食的盲源分离算法研究

李 丹，唐普英

（电子科技大学 光电信息学院，四川 成都 610054）

0 引言

盲信号处理（BSP，Blind Signal Processing）是在对源信号和传输信道信息未知的情况下，仅从观测到的混合信号中分离出源信号的一种信号处理方法[1]。盲源分离是盲信号处理的重要方面，是从上个世纪九十年代迅速发展起来的新兴领域。现有的盲源分离算法存在运算速度慢、稳定性差等方面的问题，并容易陷入局部最优，有待进一步的改进和优化。研究新的盲源分离算法是很有必要的。细菌觅食算法（BFO，Bacterial Foraging Optimization）是基于大肠杆菌觅食过程的智能优化算法，适用于优化问题的求解。它是 2002年才被提出的一种新算法，其在具体问题中的应用是很有价值的研究[2]。

1 基本原理

1.1 盲源分离的基本原理

盲源分离是在信号的来源、数目、位置及传输信道等信息都未知的情况下，直接根据观测数据对源信号进行估计。其基本思想是通过寻找一种合适的滤波器或逆系统，使得输出的信号尽可能地接近于源信号。在目前的研究中，实现分离的关键是空间的统计独立性假设，即认为源信号是相互独立的[3]。要实现信号的有效分离，还要求接收信号的个数不少于原始信号的个数。文中的研究也基于以上假设。实现分离的基本原理是：假设生成观测信号X的源信号S相互独立，寻找分离矩阵W，使输出结果 =Y WX中的各分量尽可能相互独立，则Y就是对源信号S的估计。其模型如图1所示。分离的关键是寻找分离矩阵W 。与源信号相比，分离信号的顺序和幅度都具有不确定性，但这并不影响应用。

图1 盲源分离模型

1.2 细菌觅食算法的基本原理

细菌觅食算法是一种通过模拟大肠杆菌寻找食物的过程来寻找系统最优解的智能优化算法。该算法包括如下3种操作：趋向性操作、复制操作和迁徙操作。细菌通过旋转和游动来寻找食物，在算法中，模拟这一行为的操作称为趋向性操作。根据优胜劣汰的原理，一段时间后，觅食能力差的细菌会被淘汰，剩余的细菌进行自我复制，对应到算法中即为复制操作。由于某种原因，细菌种群可能集体迁徙到新的区域，算法中与之对应的为迁徙操作，这将避免陷入局部最优，有利于寻找全局最优。该算发流程如图2所示[4]。

图2 细菌觅食算法流程

在具体应用中，细菌的位置对应解空间的解，由当前的解计算出系统适应度，根据适应度确定细菌的下一步趋向性操作。完成规定次数的趋向性操作（细菌生命结束）后，适应度较差的一半细菌被淘汰，剩下的细菌进行自我复制，然后重复趋向性操作。完成规定次数的复制操作后，原有的细菌群集体死亡，在解空间的其他位置随机产生新的细菌群，并重复上述操作，直到迁移结束。针对具体问题构造合适的适应度函数是该算法应用的关键[5-6]。

2 基于细菌觅食的盲源分离算法

根据盲源分离的概念和细菌觅食算法的原理，提出了一种基于细菌觅食的盲源分离算法。以源信号和混合信号均为两个的情况为例，选择分离矩阵W 为细菌觅食算法中解空间的解（细菌的位置），分离信号Y中两个信号的相关系数为适应度函数，相关系数越小则适应度越好。新算法步骤如下：

①初始化。设置细菌个数N、趋向性操作次数SN、复制操作次数reN 、迁徙操作次数edN 、初始适应度saveV 及各细菌的初始位置矩阵P；

②进行趋向性操作。根据细菌i的位置计算出其当前的适应度，与 Vsave作比较，若优于 Vsave，则将 Vsave的只更新为当前适应度的值，并记录此时的细菌位置为W 。然后根据比较结果确定细菌前进的方向和步长；

③进行复制操作。趋向性操作次数达到 NS后，将各个细菌趋向性操作期间的各适应度相加，并按照这个和由小到大的顺序将N个细菌排序，然后用前个细菌覆盖后个细菌，完成复制操作，再返回第②步，直到复制操作次数达到 Nre；

④进行迁徙操作。复制操作完成 Nre次后，原有的细菌群消亡，重新产生N个具有新的位置的细菌，然后返回第②步，直到 Ned次迁徙操作都完成；

⑤根据公式 Y =WX，由观测信号X和上述操作求得的W 计算出分离信号Y。

3 仿真实验

为证明新算法的可行性，对上述算法用MATLAB进行了仿真实验。两信号源分别发出方波信号和正弦波信号，如图3所示。混合矩阵为随机产生的[0，1]内均匀分布的矩阵，混合后所得信号如图4所示[7]。

图3 信号源发出信号

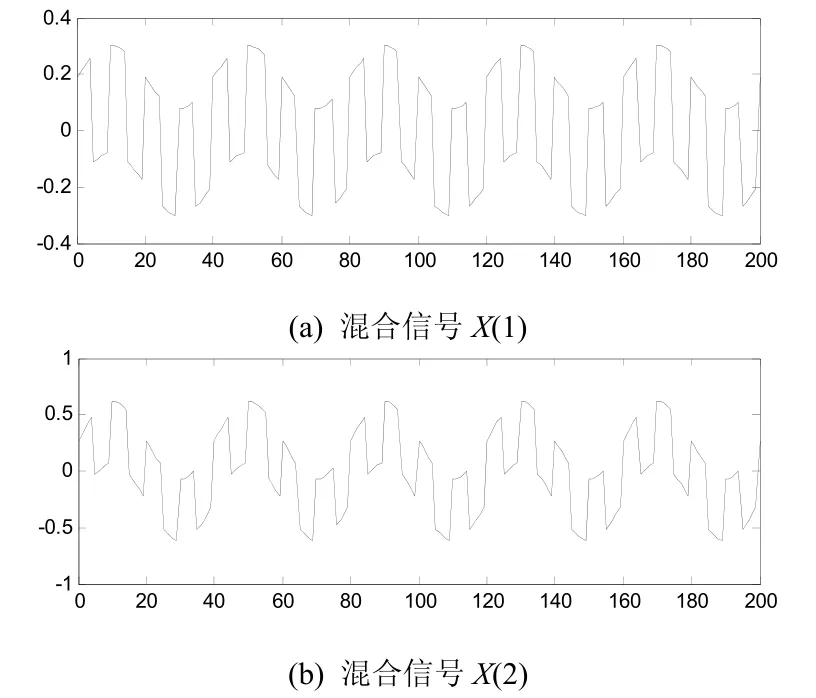
图4 混合后的信号

设定细菌总数N为10、趋向性操作次数SN 为6、复制操作次数reN 为2、迁徙操作次数edN 为2，分离结果如图5所示。作为对照，基于最大信噪比的盲源分离算法对该混合信号的分离结果如图6所示[8]。

图5 细菌觅食算法分离信号

图6 基于最大信噪比的分离算法分离信号

可以看出，图5中的波形比图6中的波形更接近于图1。也就是说，基于细菌觅食算法的分离结果优于基于最大信噪比的分离算法的分离结果。

为了更准确地说明两种分离方法的分离效果，通过计算，两种算法分离信号与源信号的相关系数分别如表 1、表2 所示。1S、2S分别表示两信号源发出的信号，1Y、2Y分别表示分离所得结果。由于分离信号的顺序和幅度具有不确定性，只需取每列绝对值最大的一个值即可。这个值的绝对值越接近 1，分离信号与源信号就越接近，则估计越准确[7]。

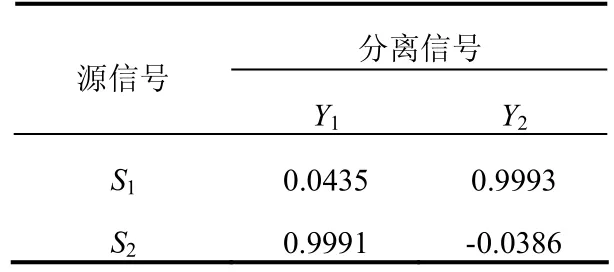
表1 细菌觅食算法分离信号与源信号的相关系数

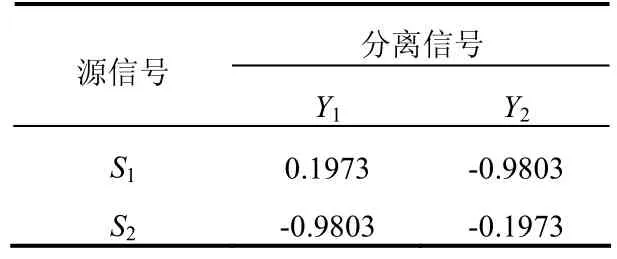
表2 传统算法分离信号与源信号的相关系数

由仿真结果可以看出，细菌觅食算法成功分离出了两路信号，且分离效果优于基于最大信噪比的盲源分离算法，证明了该算法的有效性和可行性。

4 结语

细菌觅食算法成功分离了两路线性即时混合信号，为盲源分离提供了新的研究思路。然而，目前只研究了两路信号的情况，随着信号个数的增加，需要考虑的因素就越来越多，要实现完全分离还需进一步研究。而且，分离对象仅为线性瞬时混合信号，而非线性混合信号的情形更复杂，分离难度更大，需要做更多的研究工作。另外，尚未考虑噪声的因素，在实际应用中噪声的影响又是不可避免的，所以，对含噪声的混合信号的分离也是一个进一步研究的方向。对基于细菌觅食的盲源分离的进一步研究可从以上几个方面进行[9]。

[1] 马建仓, 牛奕龙, 陈海洋. 盲信号处理[M]. 北京：国防工业出版社,2006: 85-170.

[2] 周雅兰. 细菌觅食优化算法的研究与应用[J]. 计算机工程与应用,2010, 46(20): 16-21.

[3] 赵祝兵, 周杰. 基于边检测盲源分离几何算法研究[J]. 通信技术,2008,41(10): 4-6.

[4] PASSINO K M. Biomimicry of Bacterial Foraging for Distributed Optimization and Control[J]. IEEE Control Systems Magazine,2002, 22(03): 52-67.

[5] 王雪松,程玉虎,郝名林. 基于细菌觅食行为的分布估计算法在预测控制中的应用[J]. 电子学报, 2010(02): 333-339.

[6] DELGADO A, CARVALHO J de. A Novel Multi Objective Optimization Algorithm based on Bacterial Chemotaxis [J]. Engineering Application of Artificial Intelligence, 2010, 23(03):292-301.

[7] 边峦剑. 基于改进粒子群的盲源分离算法及其应用研究[D]. 哈尔滨: 哈尔滨工程大学, 2010: 22-36.

[8] 张小兵, 马建仓. 基于最大信噪比的盲源分离算法[J]. 计算机仿真, 2006,12(10): 72-75.

[9] 权友波, 王甲峰, 岳旸,等. 盲源分离技术现状及发展趋势[J]. 通信技术, 2011, 44(04): 13-15.