仿真技术在空气蒸发器设计中的应用

程莹莹,王 浩,张 杰,柳光磊

(湖南科技大学能源学院,湘潭411201)

蒸发器是空调的换热器之一,其通过与室内冷热源进行热量交换,达到把室内的不需要的冷量或热量排放到室外的目的。蒸发器在空调系统中至关重要,因此对蒸发器的设计研究在空调器设计研究中至关重要。

制冷剂在蒸发器中主要是经历相变的过程,这样可以极好的利用制冷剂冷凝潜热大的特点。在制冷模式下,当机组系统稳定运行时,制冷剂以低温低压气液混合两相状态进入蒸发器,在蒸发器内通过吸热液态逐渐变为气态,并最终全部变为气态,乃至过热气态。当蒸发器设计不合理或系统中制冷剂充注量不够时,蒸发器内制冷剂的状态变化可能并不理想,达不到制冷效果,从而影响装置的功效。

为了能很好的反映不同情况蒸发器的特性,在建立蒸发器的数学模型时,应该充分考虑研究的目的和期待达到的效果[1]。例如,当房间空调器在运行时处于动态平衡状态,可考虑采用稳态模型;而家用电冰箱由于要不断靠开停机来动态调节冰箱内的温度,所以应当采用动态模型。在进行蒸发器特性研究时,可以通过建立复杂一些的分布参数模型,考察相关参数的分布特征,但是分布参数模型的计算量大,计算的稳定性也不易保证。

本文的研究主要是针对小型房间空调器的空气蒸发器进行的。

1 蒸发器的仿真计算模型[2]

稳态分布参数模型[3]

蒸发器稳态分布参数模型的复杂程度有很大差别,如果完全考虑流动换热的具体情况,则必须建立三维的模型。但是此类模型的计算量大,稳定性差,而且未必能保证得到令人满意的结果。故本文不考虑这些流动换热的细节,仅对主流区分为两个区域进行设计计算。

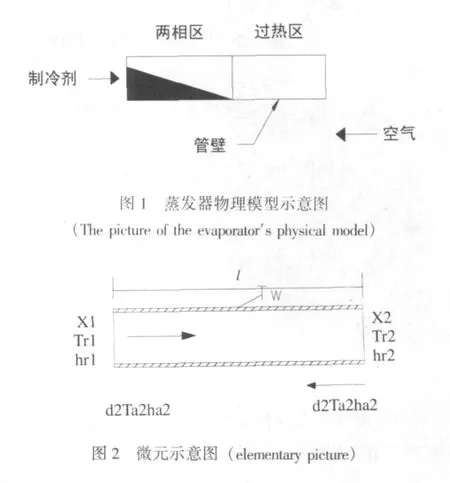
1.1 物理模型

建立蒸发器稳态分步参数模型需要在如下假设条件的基础上[4]:

1)蒸发器为逆流型换热器。常见的实际装置中制冷剂流向和管外空气的流动更接近于叉流,但是如果按照叉流计算,建立的模型就很复杂,而且按照逆流计算并不影响计算结果对实际情况的精确度。

2)管内制冷剂的流动为一维均相流动,不考虑压降[5]。实际的制冷剂流动状态因制冷剂流速较大而为复杂的分相流,但是采用最简单的一维均相模型并不会导致结果的较大差异。此处不考虑蒸发器管内压降的主要原因是因管内压降变化引起的温差并不是很大,忽略后可以使计算程序简洁明了。

3)管外空气流动视作一维流动。实际上,蒸发器管外结构复杂,空气流动受空间约束较强,但是影响与具体的装置结构有关,对于研究而言可以不考虑,根据实际的生产可以进行修正。

4)为了研究的方便,管壁热阻,管内外污垢热阻忽略不计。

5)管壁的径向温度不变。实际上蒸发器管壁上温度的分布情况很复杂,可能为线性也可能为曲线性,但是由于管壁较薄,取一个定值计算并不影响计算的精确,而且可以达到优化程序的效果。

6)其他假设条件,如忽略任何轴向的导热,管内看做无翅片结构等。

蒸发器简化后的物理模型如图1。

1.2 数学模型 (基本计算微元)

模型将蒸发器分两个相区分别来考虑:两相区和过热区。每个相区划分为若干微元。

两相区:此区中制冷剂温度不发生变化,微元按制冷剂侧焓降进行均分,当微元的个数达到一定的数值后,对计算结果的影响很小,实际计算中应具体考虑。

过热区:微元的划分按照过热区制冷剂焓差或温差进行均分。基本微元如图2所示。

对于以上任意微元,结合质量守恒定律、能量守恒定律和动量守恒定律可以建立如下的方程组:

制冷剂侧换热方程:

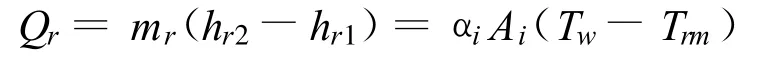
空气侧换热方程:

管内外换热量平衡方程:

制冷剂侧平均温度:

根据制冷剂侧算得管壁长度:

空气侧平均温度:

根据空气侧算得管壁长度:

对于过热区,制冷剂侧换热系数αi由Dittus-Boeler换热关联式[6]计算:

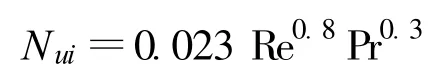
式中:

对于两相区,制冷剂侧换热系数采用Kandlikar关联式[7]:

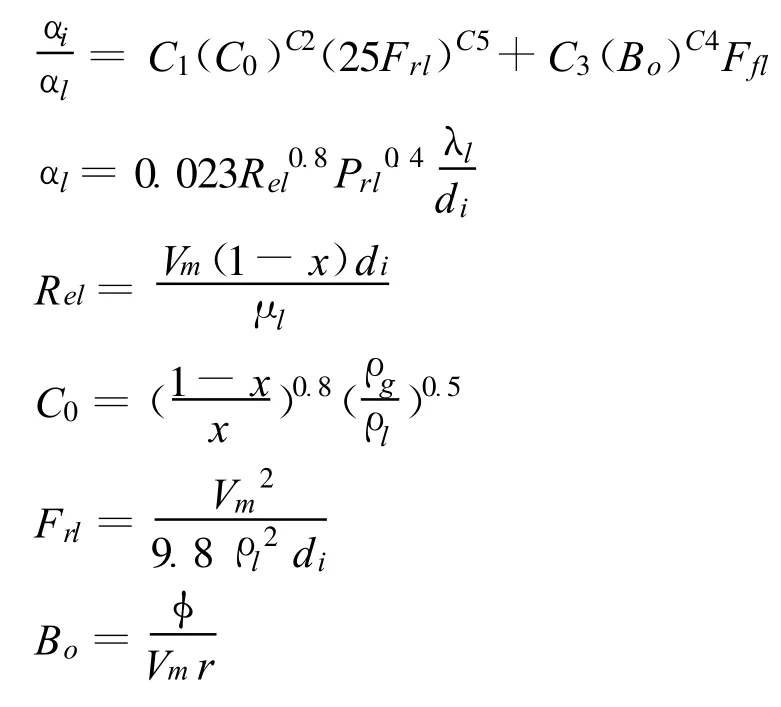
Ffl是与制冷剂性质相关的一个无量纲系数,可以按表1取值。

表 1 Ffl取值

C1～C5为常数,它们的取值取决于C0:

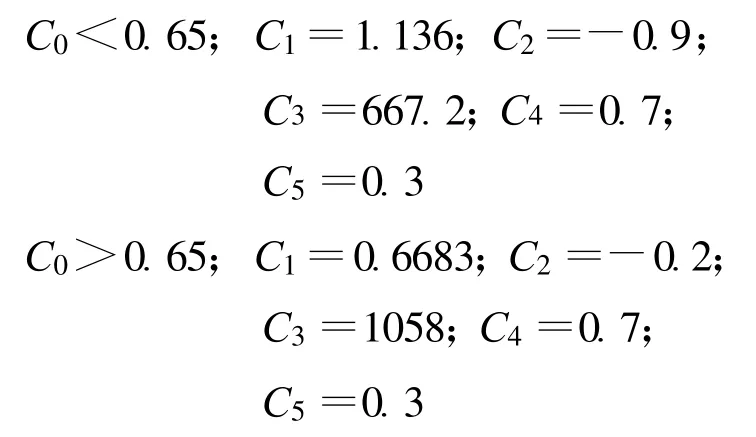
对于空气侧换热系数,采用李妩等人实验所得换热关联式如表2[8]。

计算模型应用上述关联式得到结果与实验值有一些偏差,需要根据具体的情况进一步调整。

表2 空气侧换热系数

2 算法设计

根据蒸发器换热管长度确定蒸发器出口状态参数的迭代算法[9],编制蒸发器分布参数模型计算程序。程序的输入量为蒸发器结构参数,空气和制冷剂的入口及出口条件,空气和制冷剂的流量等,这些参数在实际的使用过程中主要是建立在压缩机出厂的参数上;程序输出量为空气和制冷剂在管道中的状态,换热管的长度以及换热量。

简易程序的流程图如图3。

图3 蒸发器仿真算法流程图(The picture of the evaporator′s simulation algorithm)

3 仿真实例及结果分析

选择R22作为制冷系统制冷剂,传热管为紫铜肋管,外径10mm,内径9.3mm,四排管,每排按三角形排列,管间距25mm,沿空气流动方向管间距21.65mm,翅片间距2.5mm,翅根直径25mm。

迭代初值的确定:蒸发温度为7℃,蒸发压力为0.7MPa。由上面的程序流程图可知,程序需要的输入量如下:蒸发器出口制冷剂温度为20℃(此值可为试验测得值,用于初次迭代,根据实际情况改变),蒸发器空气入口温度35℃,相对湿度为60%。根据图表查得此状态下制冷剂和空气的其他状态参数,带入程序中进行编译。

结果及分析:

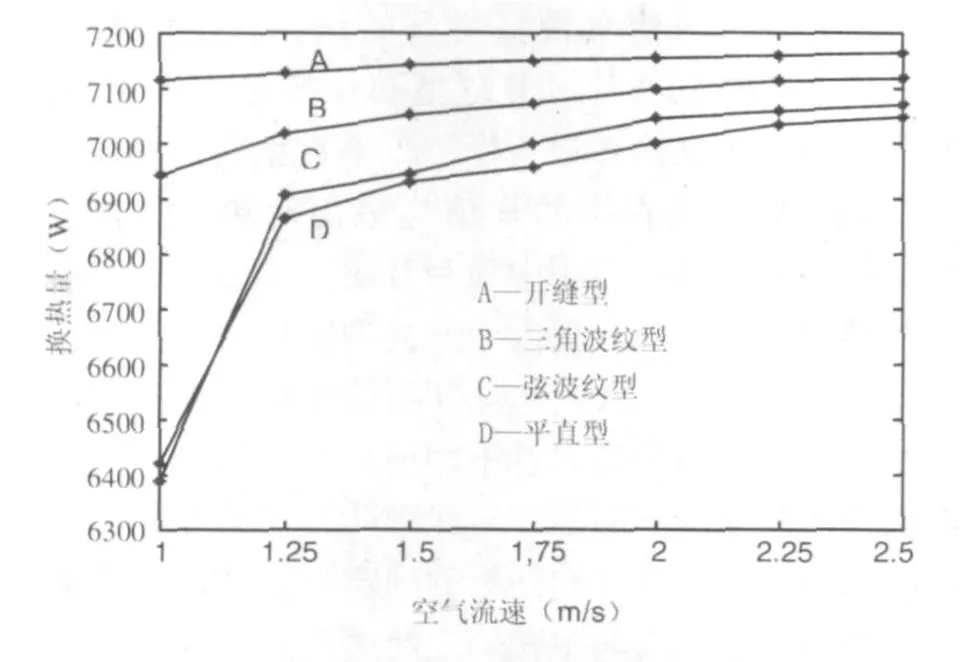
图4 不同类型肋片换热管在不同空气流速下的换热情况(The relation of the heat exchange and velocity among different types of the fins)

由图4分析可知:开缝型肋片换热效果最好,其换热量随风速变化不大,主要原因在于开缝的肋片能加大空气的扰流作用,达到强化换热的目的;三角波纹型肋片换热效果次之;正弦波纹型和平直型肋片换热效果接近。从而可以看出肋片结构的复杂性在很大程度上决定了肋片的换热效果,结构越复杂换热效果越好。但是当风流速度达到一定值之后,如图中显示的2m/s,换热能力基本不会随风度发生变化,当空气流速很小的时候,肋片结构对换热性能起着很大的作用,如图中显示1m/s的风速下,开缝型肋片换热量为正弦波纹型肋片换热量的115%。所以合理的选择肋片形式对空调换热能力有很大的关系。

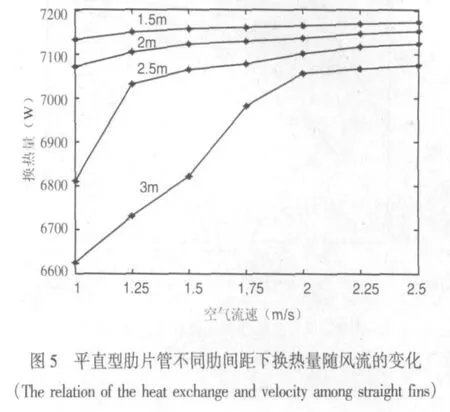
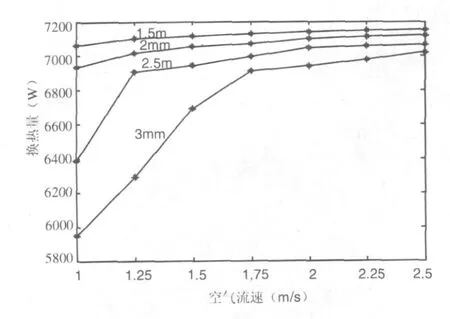
图8 正弦波纹型肋片管不同肋间距下换热量随风流的变化(The relation of the heat exchange and velocity among sine-ripple fins)

由图5至图8分析可知:肋片间距越小其换热量越大,原因在于肋间距减小后可以增大空气扰流同时增加管壁与空气的换热面积,从而增强了换热效果。但是减小肋片间距的同时会增加生产制造难度和成本,所以应综合考虑决定最终的肋间距。针对具体的肋片形式,从上面的图形分析可知,开缝型肋片肋间距的改变对换热效果没有太大的改变,平直型肋片和正弦波纹型肋片的肋间距对换热效果有一定的影响,但是影响的程度都很有限,而且当风流速度达到2m/s之后可以看到影响更加小了。

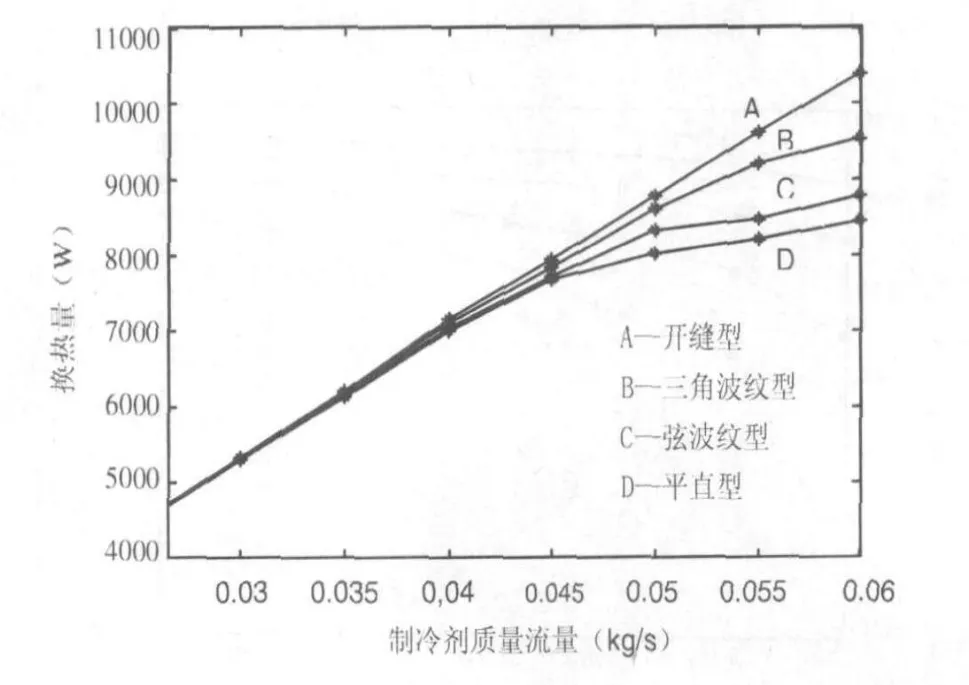
图9 不同制冷剂流量下的蒸发器换热量(The influence of the refrigerant flow making to the heat exchange)

由图9分析可知:制冷剂流量对蒸发器换热效果起着决定性的作用。当制冷剂流量较低时不管什么类型的肋片其换热效果都不好。针对具体的肋片,由图可知开缝型肋片的换热能力随制冷剂流量的变化最为强烈,流量越大,换热量就越大;另外三种肋片当制冷剂流量达到一定值 (如正弦波纹型质量流量达到0.05kg/s)之后,换热量随制冷剂流量变化就会趋缓。所以在实际的生产中要保证制冷剂流量达到某一临界值,这样就可以保证必需的换热量了。实际设计过程还应该考虑到小型制冷系统的蒸发器末端制冷剂状态,最好能使蒸发器出口的制冷剂有一定的过热度,不影响压缩机的吸气。

4 结论

(1)通过对仿真模拟得到的结果进行分析可知:四种类型的肋片以开缝型肋片换热效果最高,在各种情况下其换热最为稳定,平直型肋片换热效果最差。但是平直型肋片结构最为简单,生产方便,故现在的实际应用中最为普遍。三角波纹型肋片换热效果也很好,仅次于开缝型肋片。

(2)同一种形式的肋片其换热量随着肋间距的减小而增大,但是效果各不相同。开缝型肋片改变肋间距的效果最不明显,对此种肋片不需要特别小的肋间距。当然具体肋间距的确定应随实际情况而定,并不是缩小肋间距就一定能达到更好的效果。

(3)制冷剂流量对空调制冷有着决定性的影响,任何形式的肋片,当制冷剂流量较小时,无法得到制冷效果。而且任一形式的肋片在具体的情况下都存在一个能达到预定制冷效果的临界制冷剂流量,当流量达到此值时,没有必要继续增加制冷剂流量。同时应该考虑到小型制冷系统的蒸发器末端制冷剂状态,最好能使蒸发器出口的制冷剂有一定的过热度,不影响压缩机的吸气。

(4)仿真计算在空气蒸发器的设计中有很大的作用,合理的使用可以极大的帮助实际生产,节约成本缩短研发周期。并且能使实际生产过程中无法描述的情景数值化,易于观察调节。

符号说明:

Q—换热量;

h—焓值;

T—温度;

m—质量流率;

A—微元面积;

ξ—析湿系数;

λ—漏热系数;

λ根据实际测定,一般为0.8和1之间,冷凝器中一般取值0.9;

αi—管内沸腾换热系数,W/(m2K);

αl—液相在管内流动的对流换热系数,W/(m2K);

C0—对流特征数;

Ffl—液相弗劳德数;

Bo—沸腾特征数;

Prl—液相普朗特数;

λl—液相导热系数,W/(mK);

di—管内径,m;

Vm—质量流率,kg/(m2s);

质量流率的确定:制冷剂质量流量/某一制冷剂流向上所有并列管路的截面积之和。

x—制冷剂干度;

μl—液相动力粘度,Pa·s/m2;

ρg—气相密度,kg/m3;

ρl—液相密度,kg/m3;

φ—热流密度,W/m2;

r—气化比潜热,J/kg

下脚标:

a—空气侧;

r—制冷剂;

m—平均值;

i—管内侧

[1]丁国良,张春路.制冷空调装置仿真与优化[M].北京:科学出版社,2001

[2]刘浩.神经网络理论在空调仿真中的应用研究 [D](硕士论文).上海:上海交通大学.2000

[3]葛云亭,彦启森.蒸发器动态数学模型的建立与理论计算.制冷学报[J],1995,(1):9-17

[4]彦启森,石文星.空气调节用制冷技术[M].北京:中国建筑工业出版社,2004

[5]丁国良,张春路.制冷空调装置智能仿真[M].北京:科学出版社,2002

[6]Shah,M M.A General Correlation for Heat Transfer During Film Condensation Inside Pipes.Int J Refrig,1979,22(4):75-556

[7]Kandlikar S G.A general correlation for saturated two-phase flow boilingheat transferinsidehorizontal and vertical tubes.Journal of Heat Transfer.1990,112:219-228

[8]李妩,陶文铨,康海军等.整体式翅片管换热器传热和阻力性能的实验研究.机械工程学报,1997,33(3):81-86

[9]杨宾.制冷系统中蒸发器模型的建立和仿真分析[J].制冷,2006,25(3):51-55