溶液型浆体在岩溶裂隙中运移的动力学研究
孙克国,李术才,仇文革,许炜萍,张俊儒
(1.西南交通大学土木学院地下系,成都 610031;2.山东大学岩土与结构工程研究中心,济南 250012)
0 引言
注浆法作为一种预防和处置多种地质灾害的有效方法,在19世纪初出现以来,随着近代工业和材料学的迅速发展,注浆设备和注浆材料都得到了极大的进步。得益于工艺的完善和新材料的研制,其应用范围和堵水加固效果也得到了工程界的认可。但相对于注浆法在现场实践中的快速发展,其理论层面的研究水平却相对落后,且进展缓慢,已经不能有效指导注浆法的发展。其主要原因是被注介质的复杂性、浆液特征参数的多样性和时变性以及注浆过程的隐蔽性[1]。在注浆开始之前、注浆过程之间和注浆结束之后,随着浆液特性的改变,技术人员均难以有效把握被注介质在注浆作用下的改变。而且浆体动力学的研究涉及到牛顿与非牛顿流体动力学、岩土体力学和渗流力学等多门学科,给相关的理论研究带来很大的困难。
正因为浆液在注入过程中所表现出来的复杂特征以及被注介质的千差万别,所以必须对其进行分类研究。依据浆液被注介质中扩散机制和作用形式的不同,可以将岩土体中的注浆法分为渗透注浆、充填注浆、压密注浆、劈裂注浆和喷射注浆5种。注浆工作者以此为基础,对其进行研究,并获得了诸多的符合实际工程的有益成果,如Baker[2]和隆巴迪分别推导了牛顿流体和宾汉流体在裂隙中注浆的最大扩散半径。Wittke W等[3]推导出的公式基本与隆巴迪公式相似。杨晓东等[4]与刘嘉材[5]分别推导了未考虑黏度时变性的浆液扩散公式。阮文军[6]通过大量试验证明水泥基浆液的黏度时变性符合指数函数分布,假设浆液在裂隙岩体中的流动符合宾汉流体的层流运动,在此基础上获得了浆液扩散模型。Giovanni Lombardi[7]和杨秀竹等[8-9]基于广义达西定律和球形扩散理论获得了宾汉型和幂律型浆液在渗透注浆中的扩散半径计算公式。郝哲等[10]借助于蒙特卡洛法,以单裂隙浆液扩散公式为基础编制了浆液在岩体裂隙网络中的扩散程序;郑长成[11]通过修正宾汉浆体在光滑裂隙内的辐射流运动方程,使之适用于浆液在粗糙裂隙岩体中的层流扩散。杨米加等[12]采用实验手段对裂隙张开度、交叉角度和压力梯度在渗流注浆过程中的影响进行了研究。张良辉等[13]通过稳定压水试验反算裂隙参数,建立平面粗糙裂隙中浆液层流流动的力学模型。
综合比较各种注浆工法的理论研究,可以看出在地下水渗流力学基础上发展起来的渗透注浆理论在岩土体注浆理论中最为完备。但是其也仅仅停留在研究连续介质的层流流动层面上,对于更为复杂的劈裂注浆、充填注浆和压密注浆理论仍处于半经验状态。针对岩溶区的动水注浆理论,本文在研究前人成果及现场实践的基础上认为只有从浆液特性、运移过程和被注介质这3个方面进行综合考虑,才能有效提升岩溶区的注浆理论水平。因此本文以溶液型化学浆液为流体模型,在流体动力学的基础上推导出浆液运移过程中的控制方程并对其离散,以岩溶区的贯通裂隙或管道作为被注介质模型,在此基础上对浆液在岩溶区被注介质中的运移进行了开创性研究。
1 裂隙注浆理论研究概况
由于自然界中的一切复杂流动都可以用Navier-Stokes方程来描述,而浆液在裂隙岩体中的扩散也不例外。以x方向为例时,Navier-Stokes方程可表示为:
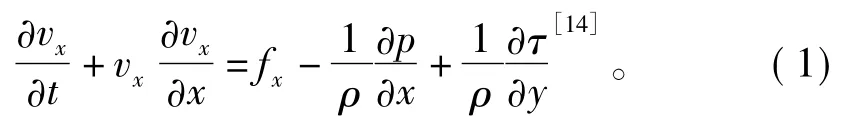
式中:f为体积力;τ为附加法向应力;vx为x方向的速度;ρ为浆液密度;t为时间;p为压力。依据浆液的物理形态可以分为溶液型和悬浮型2种,从其本构关系上讲,均属于广义牛顿流体中的宾汉流体和牛顿流体。浆液凝结或者凝胶前,溶液型浆液多为牛顿流体,悬浮型浆液多为宾汉流体。
1)当浆液是宾汉流体时
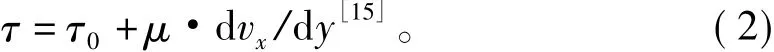
式中:τ0为驱动浆液运动的最小剪应力;μ为运动黏度;dvx/dy为剪切速率。
在黏度不变的前提下,可以求得式(1)中的平均流速vx为:
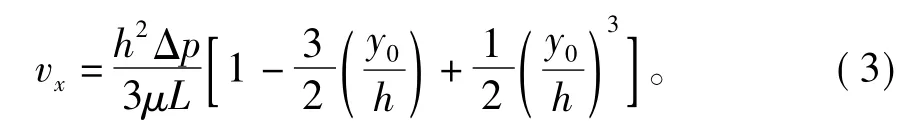
式中y0为宾汉流体的流核高度,当y=y0,τ=τ0。
2)当浆液为牛顿流体时

在黏度不变的前提下,由哈根-泊肃叶定律可以得到:
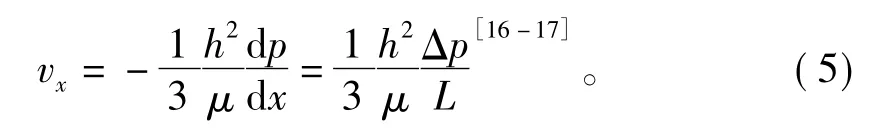
式中:p为压力;Δp为压差;L为运移距离;μ为动力黏度;h为裂隙半宽。当流核高度y0等于0时,式(3)中括号里的部分可以转化为1,此时式(3)就转化为式(5),从而验证了在牛顿流体和宾汉流体本构关系下推导出的平均速度的正确性和合理性。
通过对式(3)和式(5)的合理应用,可以获得浆液在岩体裂隙或者管道中的径向运移规律。对于裂隙辐向流可以通过对两式进行积分来获得注浆量、注浆压力、扩散半径和裂隙开度之间的关系[18]。但是式(3)和式(5)均是在小管径内液体的径向流动基础上推到演化而来,而岩体中的管道和裂隙形状多变,管道直径和裂隙开度也千变万化,如果简单以等径或等宽度的裂隙来计算,其误差将会较大的影响计算分析结果,所以在复杂的岩溶地区需要另辟它径来完成浆液在岩溶区裂隙管道中运移的研究。
2 浆液扩散的动力学控制方程
2.1 质量守恒方程
质量守恒方程是连续介质理论的基础,对于某个微小体积,可以表述为体积内的质量改变量等于进入或者流出该体积的流体质量,假设该体积表面的外法线方向为正、流入该体积的速度为正。所以质量守恒方程可以表示为:
将式(6)在微小体积上积分,可以将其化为积分表达形式,如下所示:
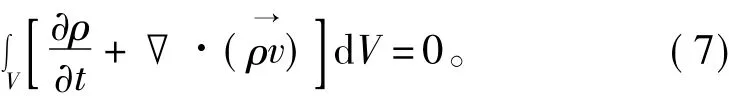
为了方便后续的离散工作,将其转化为偏微分形式,如下所示:

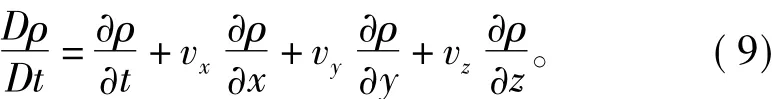
2.2 动量守恒方程
动量守恒方程是在牛顿第二运动定律的基础上推导出来的,可以表述为某个微小体积的动量随时间的变化率等于微小体积所受到的外力之和(其中i,j为张量符号)。
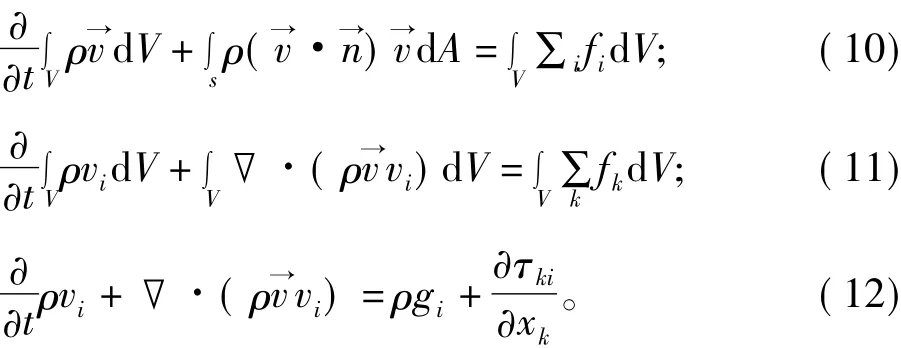
2.3 溶液浆体的动力学扩散假设
1)溶液型浆液在凝胶前一般属于牛顿流体,由于注浆过程中相对速度较低、外界压力和温度变化较小,所以可以将扩散期间的溶液型浆液视为不可压缩的牛顿流体。
2)浆液在运移过程中的锋面不与地下水发生稀释,而且其在裂隙或者管道的壁面处满足无滑移条件,即浆液在壁面上的法向和切向速度均为0。
3)岩溶管道或者裂隙的贯通性好,在浆液注入过程中无堵塞现象发生。
3 控制方程的离散格式
在上述假设的基础上,对式(8)和式(12)进行简化后,得到溶液型浆液在岩溶区裂隙或者管道中运移的动力学控制方程:
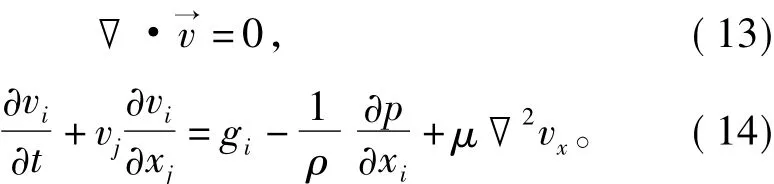
3.1 空间域的离散
3.1.1 扩散项
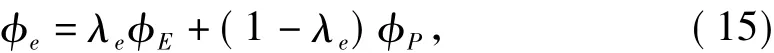
其中:
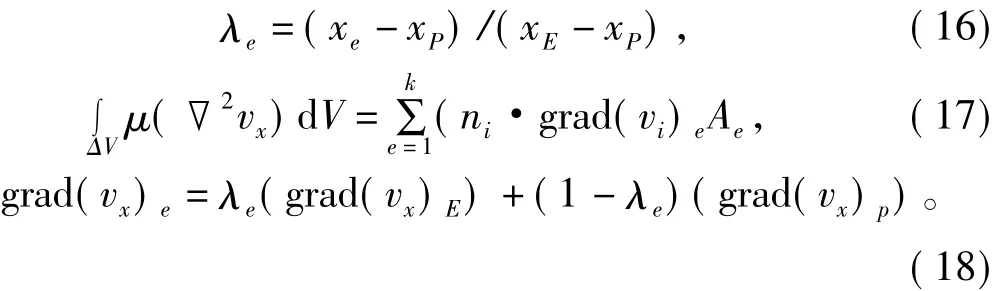
3.1.2 对流项
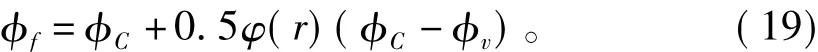
φ(r)是一个限幅函数,相当于加权函数,当φ(r)取不同的值或表达式时,式(19)可以改写为不同的插值格式,如图1和图2所示。
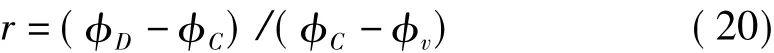
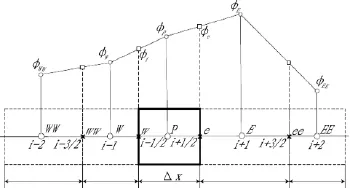
图1 Central difference示意图Fig.1 Central difference
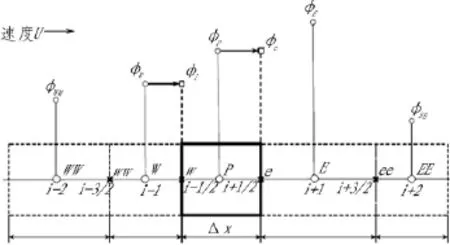
图2 HQUICK格式示意图Fig.2 HQUICK format
当 φ(r)=2(r+|r|)/(r+3)时,为 HQUICK 格式,此时的φf为:
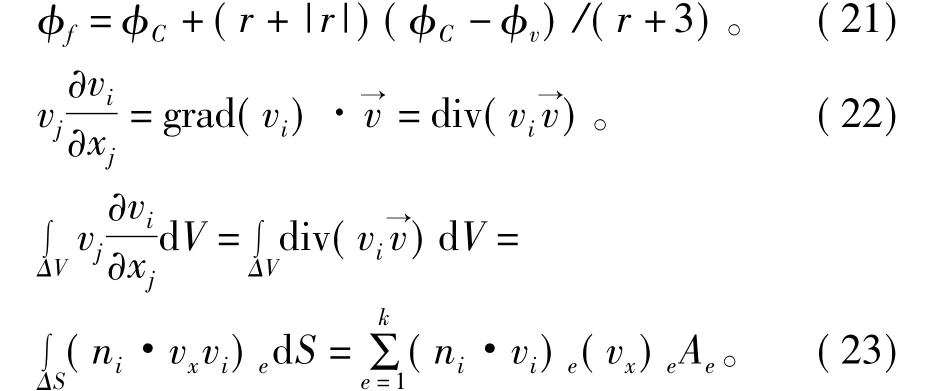
3.2 时间域的离散
为表述简便起见,动量守恒方程可以改写为:

式中:l是除去瞬态项外的所有项的算子,包括对流项、扩散项、源项。在对式(24)左右两边进行体积积分并完成空间离散后,可以表示为:

式中:L是空间域离散后的算子,包括对流项的离散、扩散项的离散以及源项的离散;V代表控制体的体积。从式(25)可以看出,对方程左边项(瞬态项)的离散不需要与右边项(对流项、扩散项、源项)保持一致,即可以对不同的项采用不同的离散格式。本文对瞬态项采用中心差分格式,对流项采用Adams-Bashforth格式,扩散项采用Crank-Nicolson格式。
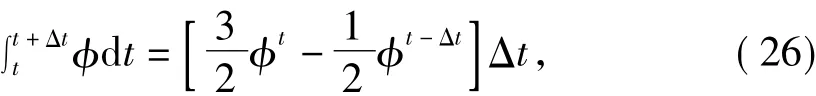
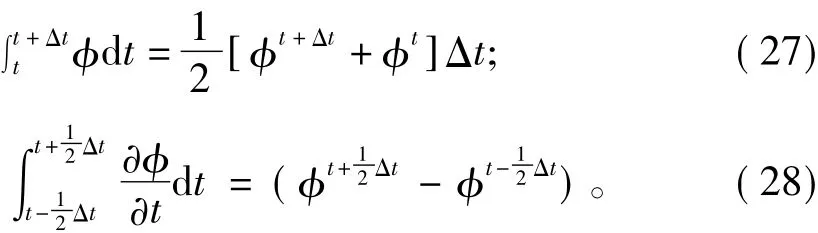
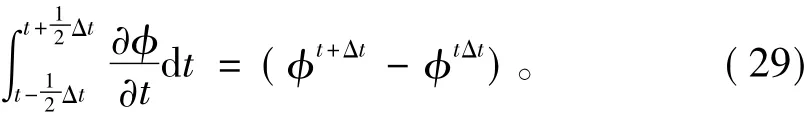
综合瞬态项、对流项、扩散项和源项的以上各种离散格式,可以得到岩溶区浆液扩散的动量守恒方程在时间域上的离散格式为:
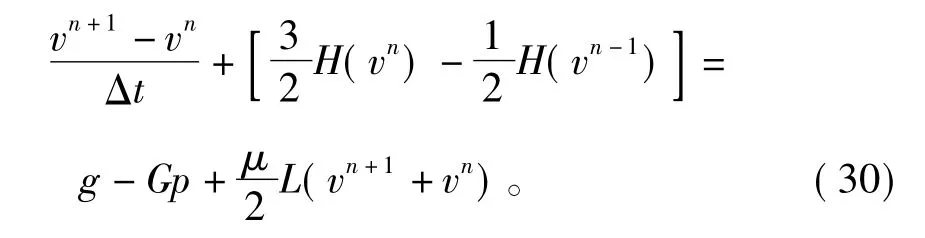
同理对于连续方程:

式中:G为梯度算子;▽为散度算子;L为拉普拉斯算子;v为速度矢量;p为压力。
4 离散方程的求解与验证
4.1 离散方程的求解
压力泊松方程法主要应用于瞬态问题的求解,是时间分裂法的一种。由于岩溶区浆液的运移过程是一个与时间具有直接关系,具有明显的瞬态特征,所以在本文的研究过程中采用压力泊松方程法来求解vx,vy,vz和p等物理量。其基本思路如下:
1)假定初始压力p;
2)利用初始压力p,求解动量守恒方程,得到不满足连续方程的速度场S*;
3)假定压力修正值p*,并用p*和S*来表示符合连续方程的速度场S,S=S*-ΔtGp*;
4)将S代入连续方程,从而得到关于p*的泊松方程,Lp*=DS*/Δt;
5)求得p*,并更新压力pnew和速度场S,pnew=p+p*,S=S*-ΔtGp*。
6)将pnew作为初始压力,进行下一时间步的计算。式中:G为梯度算子;D为散度算子;L为拉普拉斯算子。
4.2 有效性验证
笔者以此方法为基础,采用Matlab高级编程语言编制了浆液在裂隙岩体中的扩散程序(GSK)。为了验证该方法的正确性,在有限体积法的基础上,以方腔顶端驱动流为验证模型[19],将计算结果与试验结果进行验证(如图3所示),证明了该方法的正确性和精确性。
5 结论
1)总结前人关于浆液在岩体裂隙中渗流的运移形态规律,指出该规律的局限性,并从中发掘出溶液型浆体在岩溶区裂隙和管道中进行动力扩散的理论研究切入点。

图3 计算结果与试验结果对比图Fig.3 Comparison and contrast between calculation results and testing results
2)以需找的理论研究切入点为突破口,基于流体动力学基础,在质量守恒定律和动量守恒定律的指导下,推导出适用于浆液扩散的动力学控制方程。
3)针对溶液型浆液的基本特征和岩溶区被注介质所独有的特性,在对浆液扩散过程进行合理假设的基础上,通过简化浆液扩散的通用动力学控制方程,获得了适用于牛顿浆体在岩溶裂隙或管道中的扩散的动力学控制方程。
4)采用 HQUICK、Central-Difference、Crank-Nicolson和Adams-Bashforth格式对浆液在岩溶裂隙中运移的动力学控制方程分别在时、空域上完成数值离散研究,最后采用流场分离变量求解技术中的压力泊松方程法完成数值求解工作,编制求解程序,并完成该程序的正确性和精度验证工作。
5)在流体动力学的基础上,对溶液型浆体在岩溶裂隙和管道中的动力学扩散过程进行开创性研究。但是此过程没有考虑浆液的黏度时变性,也没有对符合悬浮型浆液的宾汉流体的动力学控制方程进行数值离散求解,这将是下一步的研究重点。
[1] 王杰,杜嘉鸿.岩土注浆技术的理论探讨[J].长江科学院院报,2000,17(6):82-86.(WANG Jie,DU Jiahong.Theoretical exploration on grouting technology[J].Journal Of Yangtze River Scientific Research Institute,2000,17(6):82-86.(in Chinese))
[2] Baker C.Comments on paper‘Rock Stabilization in Rock Mechanics’[A].Muler,Springer-Verlag NY,1974.
[3] Wittke W.采用膏状稠水泥浆灌浆新技术[C]//现代灌浆技术译文集.北京:水利电力出版社,1991:48-58.(Wittke W.The application of grouting with dense cement paste[C]//In collection of translations of modern grouting techniques.Beijing:Water Resources and Electric Power Press,1991:48-58.(in Chinese)
[4] 杨晓东,刘嘉材.水泥浆材灌入能力研究[C]//中国水利水电科学院科学研究论文集:第27集.北京:水利电力出版社,1987:184-191.(YANG Xiaodong,LIU Jiacai.Groutability of cement grouts[C]//Scientific symposium of the institute of water resources and hydropower research:27th.Beijing:Water Resources and Electric Power Press,1987:184-191.(in Chinese))
[5] 刘嘉材.裂缝灌浆扩散半径研究[C]//中国水利水电科学院科学研究论文集:第8集.北京:水利出版社,1982:232-233.(LIU Jiacai.Study on the diffusion radius of grouts in the rock fracture[C]//Proceedings of the eighth scientific research symposium of China Institute of Water Resources and Hydropower Research:8th.Beijing:China Waterpower Press,1982:232-233.(in Chinese))
[6] 阮文军.浆液基本性能与岩体裂隙注浆扩散研究[D].长春:吉林大学地质工程系,2003.(YUAN Wenjun.Research on diffusion of grouting and basic properties of grouts[D].Changchun:Geoloy Engineering,Jilin University,2003.(in Chinese))
[7] Giovanni Lombardi Grouting of rock masses[C]//Grouting and Ground Treatment:Proceedings of the Third International conference(GSP 120).ASCE,2003.
[8] 杨秀竹,雷金山,夏力农,等.幂律型浆液扩散半径研究[J].岩土力学,2005,26(11):1803-1806.(YANG Xiuzhu,LEI Jinshan,XIA Linong,et al.Study on grouting diffusion radius of exponential fluids[J].Rock and Soil Mechanics,2005,26(11):1803-1806.(in Chinese))
[9] 杨秀竹,王星华,雷金山.宾汉体浆液扩散半径的研究及应用[J].水利学报,2004(6):75-79.(YANG Xiuzhu,WANG Xinghua,LEI Jinshan.Study on grouting diffusion radius of Bingham fluids[J].Journal of Hydraulic Engineering,2004(6):75-79.(in Chinese))
[10] 郝哲,王介强,何修仁.岩体裂隙注浆的计算机模拟研究[J].岩土工程学报,1999,21(6):727-730.(HAO Zhe,WANG Jieqiang,HE Xiuren.Computerized simulation of crack grouting in rock mass[J].Chinese Journal of Geotechnical Engineering,1999,21(6):727-730.(in Chinese))
[11] 郑长成.岩体裂隙内稳定水泥浆液扩散范围的理论分析[J].水利与建筑工程学报,2006,4(2):1-5.(ZHENG Changcheng.Estimation on penetrating radius of stable cement grouts in rock fractures[J].Journal of Water Resources and Architectural Engineering,2006,4(2):1-5.(in Chinese))
[12] 杨米加,陈明雄,贺永年.裂隙岩体注浆模拟实验研究[J].实验力学,2001,16(1):105-112.(YANG mijia,CHEN Mingxiong,HE Yongnian.Simulating experiment for grouting seepage in rockmass[J].Journal of Expermental Mechanics,2001,16(1):105-112.(in Chinese))
[13] 张良辉,熊厚金,邹小平,等.平面裂隙参数计算机器对浆液流动的影响分析[J].岩土力学,1998,19(1):7-12.(ZHANG Lianghui,XIONG Houjin,ZOU Xiaoping,et al.Calculation of the parameters of fissure and analysis of grout flowing in the fissure[J].Rock and Soil Mechanics,1998,19(1):7-12.(in Chinese))
[14] Tasos C.Papanastasiou,Georgios C.Georgiou.Viscous fluid flow[M].Washington,D C:CRC Press,2000.
[15] 沈崇堂,刘鹤年.非牛顿流体力学及其应用[M].北京:高等教育出版社,1989.(SHEN Chongtang,LIU Henian.Mechanics of non-newton fluid and application[M].Beijing:Higher Education Press,1989.(in Chinese))
[16] Frank M White.Viscous fluid flow[M].2nd edition.McGraw-Hill,Inc,1991.
[17] H Schlichtinq,K Gersten.Boundary-layer theory[M].8th edition.Springer,2000.
[18] 郝哲,王介强,刘斌.岩体渗透注浆的理论研究[J].岩石力学与工程学报,2001,20(4):492-496.(HAO Zhe,WANG Jieqiang,LIU Bin.Theoretical study of osmotic grouting in rock mass[J].Chinese Journal of Rock Mechanics and Engineering,2001,20(4):492-496.(in Chinese))
[19] E Erturk,T C Corke,C Gokcol.Numerical Solutions of 2D Steady Incompressible Driven Cavity Flow at High Reynolds Numbers[J].International Journal for Numerical Methods in Fluids,2005,48:747-774.

