大型干坞放排水过程中边坡稳定性分析
宋 妍,王光辉
(中铁隧道集团有限公司技术中心,河南洛阳 471009)
0 引言
目前,国内外大型干坞放排水施工监测参考分析资料十分稀少,相关领域的文献资料对此种工况的参考价值也是十分有限。文献[1-2]肯定了ANSYS计算软件在渗流分析中的有效性,并依托工程实例进行验证,同时涉及到了水头、渗透系数及含水量等影响因素的分析;文献[3]利用有限元的方法分析了受雨水浸润的边坡和路肩应力、应变情况,找出雨水浸润和车辆荷载对边坡失稳和路肩破坏的影响程度,从而为牧区道路的设计提供相关理论依据;文献[4]探讨了堤防土质在浸水后强度指标的变化规律及堤防稳定情况,并对洪水长时间浸泡后堤防的各项指标进行了预测;文献[5]分析了水位升降、降水、裂隙等因素对堤防安全的影响规律。文献[1-5]从各个角度分析边坡与内外水的相互作用,但均缺乏实际现场监测数据的有效支持,并且干坞内边坡放排水速率有别于降水及洪水。以生物岛—大学城沉管隧道施工为例,对大型干坞放排水过程中边坡的稳定进行数值模拟计算并对现场监测数据进行分析总结。
1 工程概况
生物岛—大学城隧道工程位于广州市的东南部,连接生物岛与大学城,隧道线路呈南北走向。本标段为A标段,A标段工程的起讫里程为SK0+265~+817,全长552 m,包括214 m的沉管段和338 m的北端岸上段。在北端边岸上段基坑内,能满足一次性预制全部3节管段和北端27.5m接口段主体施工的场地需要。214 m的沉管段分为E1,E2和E3 3节管段,每节管段的长度分别为94,116,4 m。设计采用北端轴线干坞方案,坞底标高为-5.61 m,接头段主体结构标高和坞底标高能够错开,在高潮位时满足管段浮运出坞要求,最后完成273 m明挖暗埋管段施工。
北端岸上段基坑东侧为土质边坡,由上到下依次为人工覆土、〈3-2〉粉细砂、〈5-1〉砂质黏性土(残积-可塑)、〈5-2〉砂质黏性土(残积-硬塑)及〈6〉全风化层。放坡开挖支护形式主要有预应力锚网喷支护、预应力锚杆、预应力锚索,坡面设有排水孔,边坡施作过程中应注意保护边坡原状土。放坡开挖挂网喷射混凝土厚度为100 mm和120 mm,网片约21000 m2,混凝土量约为2 200 m3;预应力锚杆采用直径16~18 mm锚杆,间距1 300~1 500 mm,长度为6~28 m,倾角20°,总长度约为77 600m;预应力锚索采用2~4根钢绞线,每根钢绞线由直径5 mm的7根盘条组成,间距1 200 m,长度为20 ~36 m,倾角分别为20°,30°和45°,总长度约为28200m。西侧为旋喷桩和钻孔灌注桩桩锚支护。干坞西侧旋喷桩有131根,直径800mm,间距1200mm,深度为13 m,总长度为1 703 m;干坞端头(接口段,即东侧)钻孔灌注桩有30根,直径800 mm,间距1 200 mm,深度为11~24 m,总长度为482 m;干坞西侧钻孔灌注桩有130根,直径1 000 mm,间距1 200 mm,深度为17 m,总长度为1 870 m。
东侧土质边坡经历放坡开挖、管段制作、管段浮运、边坡二次开挖等复杂工况,为国内施工监测少见项目。
2 数值模拟方案及结果分析
2.1 数值模拟方案
边坡稳定分析的计算方法有很多,如条分法、数值分析方法、塑性极限方法、可靠度方法和模糊数学方法等。目前,对于土质边坡来说,边坡稳定分析方法主要分2类,即以极限平衡理论为基础的条分法和以弹塑性理论为基础的数值计算方法。
ANSYS是一个功能强大的有限元软件,边坡稳定分析就是利用ANSYS可对结果数据进行数学运算的功能来做的,即:根据有限元程序计算得到的应力场来计算各点的安全系数,然后利用ANSYS强大的后处理功能绘出安全系数等值线,安全系数最小的那条等值线就是最可能的滑裂面,其安全系数就是边坡的安全系数。
求出了各点(在ANSYS中实际上是各单元的高斯积分点)安全系数F后,就可以用ANSYS绘出F的等值线图。F>1部分的抗滑力大于滑移力,是稳定的。F<1部分如果等值线穿越凌空边界,则这部分不但有滑移的趋势而且有滑移的可能,是不稳定的,且F等值线就是滑移线;F<1的部分如果等值线成为封闭曲线或与固定边界成为封闭曲线,其包围的部分虽有下滑的趋势,但封闭区域以外的部分是不滑动的,所以封闭区域以内的部分受外面部分的约束也没有滑移的可能,仍然是稳定的。如果所有的F都大于1,则最小的F就是该边坡的稳定安全系数[1]。
ANSYS没有直接进行渗流分析模块,但可以用热分析模块进行渗流分析。土体渗流问题与温度场问题的控制方程与定解条件在数学上是一样的,只需要将温度场介质换成土体介质,相应的参数换为求解渗流场的参数,就可以采用ANSYS软件中温度场分析功能进行渗流场的分析计算。
2.2 数值模拟结果分析
边坡内部水头值均采用实测数据,边坡内外水位差选取抽水过程中的最大值进行模拟,即边坡内水位为0.06 m,边坡外水位约为-5.0 m。干坞底部淤泥以荷载形式作用在坡脚处。边坡岩土力学参数如表1所示,模拟时渗透系数以埋深函数形式定义。
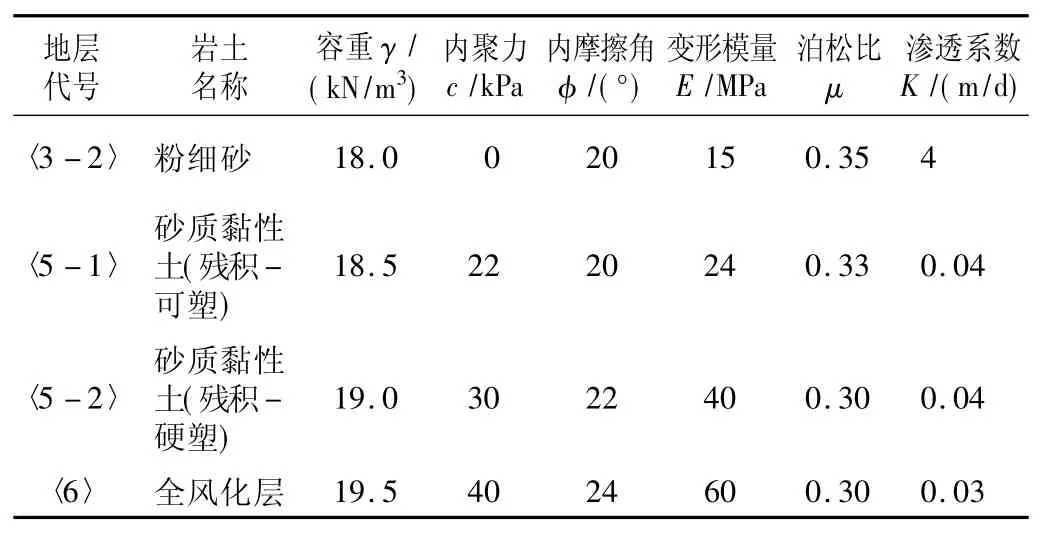
表1 岩土层力学参数表Table 1 Mechanical parameters of rock and soil strata
图1为受静水压力作用下边坡的变形。图2为利用ANSYS温度场对边坡进行的渗流分析。鉴于渗流场与应力场耦合带来的诸多不便及误差,本次模拟尝试提取图1中各节点水头值,重新建立模型后,将各节点的水头值转化为渗透力作用在新模型相对应的节点上,计算结果如图3所示。
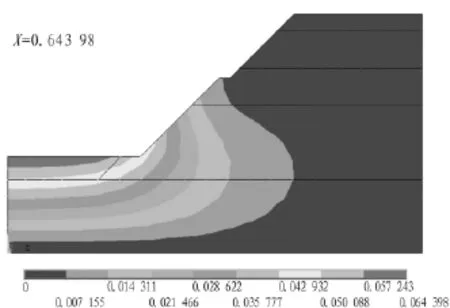
图1 干坞放水后边坡变形(单位:m)Fig.1 Slope deformation after water filling(m)

图2 边坡渗流分析(单位:m)Fig.2 Analysis on slope seepage(m)
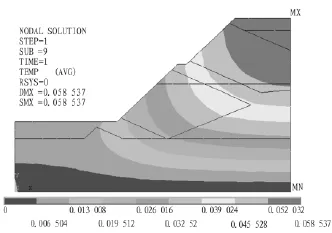
图3 干坞排水后边坡变形(单位:m)Fig.3 Slope deformation after water discharging(m)
图中3条水平台由下向上分别称为坞底、8.3 m平台及边坡顶部。水头值沿Y轴方向,水位测点设在8.3 m平台上,最高水头设定是以实测数据为检验标准,通过反复计算确定在边坡顶部附近的32.7 m。图4中边坡最小安全系数为1.08,在坞底和边坡顶部,对边坡稳定没有构成威胁。8.3 m平台下有若干条潜在滑裂面,因安全系数均大于1.3,故可认为干坞排水对边坡稳定没有影响。
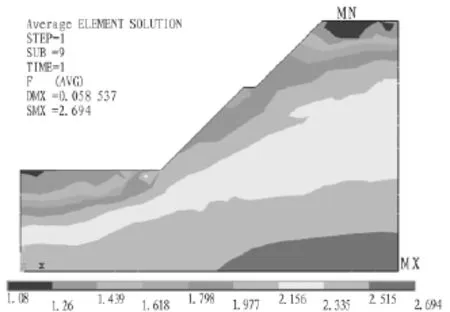
图4 边坡安全系数计算Fig.4 Calculation of safety factor of slope
3 现场监测分析
干坞2009年2月18号放水,第1阶段放水至高程1.6 m处进行管段检漏(低水位检漏);2月27日,干坞第2阶段放水至高程5m处(高水位检漏)。边坡内水位从2009年2月19号开始明显上升,直到2009年3月12号上升到5m左右,与干坞内水位基本持平。
干坞及测点布点如图5所示,测点布置在8.3 m平台上。
图5 干坞及水位孔布点Fig.5 Dry dock and layout of piezometer holes
3.1 干坞内放水
2009年2月19号至2月22号边坡内水位变化明显,4 个水位孔内水位累计变量分别为 4.65,4.50,4.50和4.57m,水位平均上升速度分别为0.93,0.90,0.90 和0.91m/d。至2009年2月22日边坡内水位约为1 m,稍低于干坞内水位1.6 m。2009年2月23号至2月27号,水位变化趋向于平缓,4个水位孔水位累积变化量分别为0.91,1.14,0.91 和0.76 m,水位平均上升速度分别为 0.18,0.23,0.18 和 0.15 m/d。2 月 27 日,干坞继续放水至高程5 m处,2009年2月27日至3月1日边坡内水位上升速度小于第1阶段,4个水位孔内水位平均上升速度分别为 0.68,0.67,0.62 和 0.62 m/d。至2009年3月1日,边坡内水位约为4 m左右。从2009年3月2日开始水位上升速度减缓,2009年3月2日至2009年3月18日,12d 4个水位孔内水位累积变化量分别为 0.78,0.75,0.91 和0.66 m,水位平均上升速度 0.065,0.062,0.076 和 0.055 m/d。至 2009年3 月18 日,4 个观测点内水位分别为4.78,5.00,4.97和5.02 m,基本持平于干坞内水位。可见,水头是影响边坡内水位上升速率的主要因素,第1,2阶段水头分别约为7.2和3.4m;排水孔对边坡内水位提升有助力作用;锚网喷混凝土层具有一定的防水能力。边坡内水位历时曲线如图6所示。
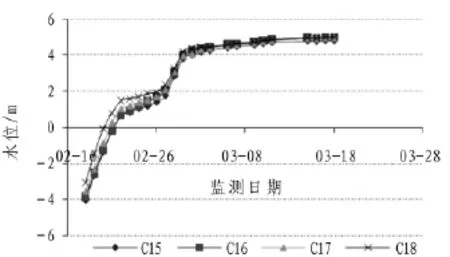
图6 放水期间边坡内水位历时曲线Fig.6 Curves of water head inside slope during water filling
3.2 干坞内排水
坞门破除后,干坞基坑内的水与官州河连成一整体,基坑内水位每天随官州河潮汐涨落而波动,此时边坡内的水位也会有一些变化,如图7所示。官州河涨潮时,基坑内的水位升高,边坡内的水位也随之升高,且升高速度很快,基坑内水位稍微高于边坡内的水位,但相差不大;官州河落潮时,基坑内的水位降低,边坡内的水位也随之降低,但降低速度较慢,基坑内水位明显低于边坡内的水位。同时,C18水位孔靠近接口段,与其他水位孔相比,多了一个方向的水源供给,在潮汐涨落过程中,该孔的水位相比其他水位孔的水位处于极端位置。图7中监测16次之前是每天高低潮汐时测得的边坡内水位,高潮汐时边坡内最高水位达5.72 m,低潮汐时边坡内最低水位为5.05 m,时测管州河高潮汐为5.8 m,低潮汐为4.5 m,可见坡外水体进入边坡的速度大于边坡内水体流失的速度。
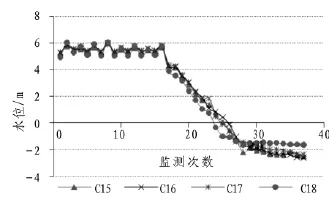
图7 排水期间边坡内水位历时曲线Fig.7 Curves of water head inside slope during water discharging
二次围堰选择在官州河低潮位时封闭,有效减少基坑内排水的工作量。在基坑排水的过程中,监测基坑内、外水位的变化速度,以边坡内(基坑外)水位降低的速度来控制下一步基坑内排水速度。基坑内外水位及差值的曲线如图8所示。由图8可知:在基坑内排水的同时,边坡内的水位也明显降低,但边坡内水位降低速度明显慢于坑内水位降低速度。随基坑排水,边坡内外水位差在逐步增大,由最初的平均1 m到平均3 m,为保证边坡安全,加密监测的同时减少日抽水量;抽水结束后边坡内水位仍有少许下降。
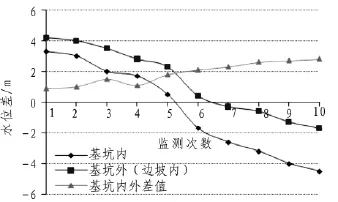
图8 基坑内外水位及差值的曲线Fig.8 Curves of water heads inside and outside foundation pit and their differences
3.3 边坡放排水期间变形分析
H1~H11均匀分布在8.3 m平台之上,H1始于边坡始端接口段,H11靠近边坡尾端桩锚支护段。现场采用H2~H10监测数据分析,如图9所示。边坡始端变形小于边坡尾端变形,分析原因在于H2靠近的接口段采取地下连续墙及交叉锚索施工,相当于重力式挡土墙给予边坡始端很好的保护,相比之下H10附近的桩锚支护对边坡尾端的保护欠之。对比干坞放水期间边坡内部水位,如图7所示,边坡H10点处的沉降与水位变化基本同步;如图10所示,经过近半年的浸泡,于9月16日干坞开始排水到24日结束,边坡沉降基本与图7中水位变化同步,排水结束后边坡变形趋于平稳。
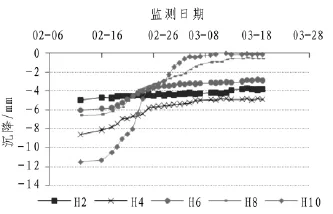
图9 边坡放水期间边坡沉降Fig.9 Slope settlement during water filling
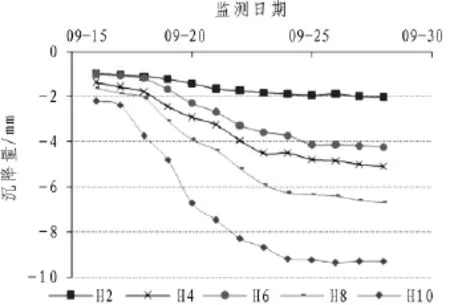
图10 边坡排水期间沉降历时曲线Fig.10 Slope settlement during water discharging
数据显示边坡在干坞放水期间的最大变形(11.31 mm)大于干坞排水期间的最大变形(-9.86 mm),由于现场没有对边坡土体进行放排水前后力学试验,无法确切判断边坡在水中长期浸泡后力学参数的改变情况,参考相关资料,分析原因有三:1)土体弹塑性。当边坡放水时,在超过0.1 MPa的静水压力作用下,边坡局部土层产生塑性变形,而大部分土体还处于弹性变形范围内;当边坡排水时,塑性变形无法完全恢复,但弹性区变形可以恢复,所以抽水后边坡的累计变形小于放水时期边坡的累计变形。可以假设,外部水体浸入为边坡的“吸”,内部水体渗出为边坡的“吐”,如果边坡再次“吸吐”水体,边坡的累计变形量差会逐步衰减下去。2)静水压力。水侵入边坡内部后,尽管会使之自重增加,但静水压力的推挤作用更加强大使之向坑外变形,使累积变形逐步恢复。3)有效应力。土中总应力是不变的,放水时孔隙水压力增大,有效应力较之前减小,边坡有恢复原状态的趋势;排水时孔隙水压力减小,有效应力增大,迫使土体产生较大变形。因土体中没有蒙脱石等遇水膨胀的土质,所以不在考虑范围内。
4 结论
1)由于参数选取、施工效果、支护等不确定因素,使有限元软件在岩土数值模拟方面存在很大困难。以本工程为例,尝试在没有渗流场与应力场耦合的情况下,将渗流场计算得到的水头转换为结构场下的渗透力,计算边坡的稳定性,但从边坡变形量与实际对比,此种方法仍有不成熟处。
2)点安全系数法在计算边坡稳定性是可行的,但准确程度有待进一步调试。
3)ANSYS模拟边坡锚杆锚索支护,通过提高周边土体参数来实现,参数具体数值与实践经验关系密切。
4)干坞放、排水2个阶段,边坡几乎同时完成对水的“吸、吐”过程。“吸水”过程中边坡变形大于“吐水”过程中边坡的变形,并且边坡的“吸水”速度大于“吐水”速度,由于边坡持水能力,造成边坡内外水差局部最大达4 m,对边坡稳定造成威胁。
5)不同于堤坝水位的频繁迅速升降,干坞排水的速率对边坡稳定性有极大的影响。
6)基坑内水体对边坡的反压效果,可以有效较小边坡的不利变形。
7)边坡内部渗流并未对边坡稳定造成危害,微量流砂未对边坡土体的强度造成影响。
8)在控制边坡滑动时锚杆、锚索可以被动的发挥作用,而控制边坡的变形则十分有限。锚杆、锚索提高了潜在滑动面土体的整体性及强度,也使边坡土体内部刚度不连续,致使局部出现较大的屈服应力和变形。
9)边坡两翼历史累积变形大于边坡中部。在边坡内外水作用下,由于边坡两翼约束方式不同,使之因“吸、吐”水产生的变形也有差异。
[1] 李维维.用ANSYS作考虑渗透压的边坡稳定分析[D].贵阳:贵州大学水工结构工程,2006.
[2] 黄燕宏.渗流及其对边坡稳定性影响的有限元模拟分析[D].武汉:华中科技大学岩土工程,2006.(HUANG Yan-Hong.Simulation analysis with FEM on seepage and its infulences to stability of the dam slop[D].WuHan:Geotechnical Engineering,Huazhong University of Science & Technology,2006.(in Chinese))
[3] 胡朋,李万鹏,柳志军.雨水浸润对牧区道路边坡稳定性的影响[J].山东交通学院学报,2005,13(1):40-44.(HU Peng,LI Wanpeng,LIU Zhijun.The influence of rain soaking on the stability of pastoral area highway slope[J].Journal of Shandong Jiaotong University,2005,13(1):40-44.(in Chinese))
[4] 乔兰,赵宇坤,李庆安.考虑洪水浸泡的黄河下游堤防稳定性预测[J].人民黄河,2008,30(7):14-17.(QIAO Lan,ZHAO Yukun,LI Qing’an.Predict stability of immersed embankments of the lower[J].Yellow River,2008,30(7):14-17.(in Chinese))
[5] 沈华中,洪卫.基于GeoStudio软件的堤坝安全评价[J].人民黄河,2008,30(11):18-20.
[6] 龚曙光,谢桂兰.ANSYS操作命令与参数化编程[M].北京:机械工业出版社,2004.
[7] 龚曙光.ANSYS基础应用及范例解析[M].北京:机械工业出版社,2003.
——结构相互作用的影响分析

