购票问题的数学模型研究

韩新社

（武汉船舶职业技术学院公共课部，湖北武汉 430050）

问题 在一场激烈的足球赛开始前，售票工作正在紧张地进行中。每张球票50元。现有2n个人排队购票，其中有n个人手持50元的钞票，另外n个人手持100元的钞票，假设开始售票时售票处没有零钱。问这2n个人有多少种排队方式，才不致使售票处出现找不开钱的局面？

解法一，从题目中可以推断出，只有手持100元的人才需要找50元。也就是说，当手持100元的球迷到达售票处时，售票处至少一张50元的零钱。不难看出，从队首开始往后数，任何时候，只要手持100元球迷总数比手持50元的球迷少，就肯定可以把钱找开。从这个问题可以联想到括号匹配问题。假设每个手持50元的球迷是一个左括号“（”，而手持100元的球迷是右括号“）”，要求任意一个左括号都要有一个右括号与它对应。类似的，任意一个手持100元的球迷，他从售票处找回的50元都来自于他之前一个手持50元的球迷。所以，始终找得开钱的排队方式对应着合法的括号排列。

根据解决括号匹配问题的思路，可以考虑用栈来解决问题。假设存在一个栈，遍历n个左括号“（”和n个右括号“）”排成的队列，每次如果是左括号“（”，则将其压人栈中；如果是右括号“）”，则让栈尾的左括号“（”出栈，如果能够始终保持栈中有足够的左括号，那么该排列是一个合法排列。

因此，可以做如下分析。第0个符号一定是左括号，否则该队列肯定出错。假设第0个左括号跟第k个符号匹配，那么从第1个符号到第（k－1）个符号，第（k＋1）个符号到第（2n－1）个符号也都是一个合法的括号序列。可想而知，k肯定是奇数。否则，第2个符号到第（k－1）个符号之间只有奇数个符号就不合法，设k＝2i＋1（i＝0，┄，n－1），如图1所示。

图1 括号排列示意图

假设2n个符号中合法的括号序列个数为f（2n），若第0个括号（左括号）与第k＝2i＋1（i＝0，┄，n－1）个括号（右括号）匹配，那么剩余括号的合法序列为：f（2i）·f（2n－2i－2）个，根据上面的分析，可以得到如下递推式：

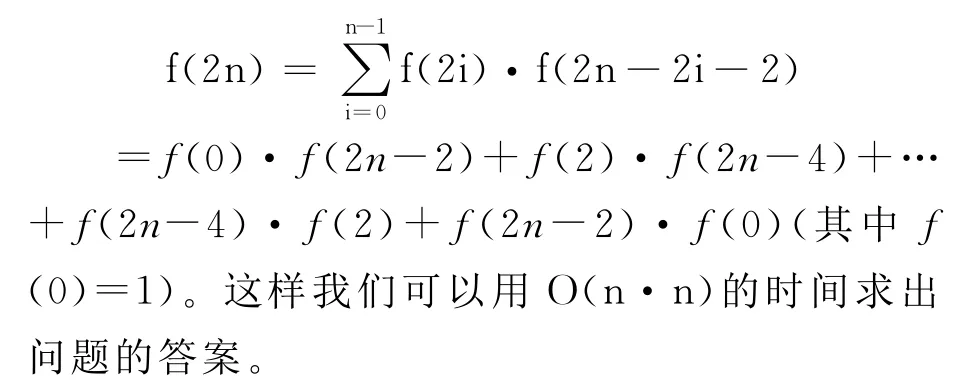
解法二，为了便于描述，这里用1表示持有50元的球迷，用0表示持有100元的球迷。那么2n个球迷的排队就对应n个1和n个0的排列，例如：1，1，0，0，0，┄，1。如果序列的任意前k（k＝1，2…，2n－1）项中1的个数都不少于0的个数，我们称这样的一个序列是合法的，否则称其为非法序列。显然合法的序列正好与可行的排列方式一一对应。同时，定义由（n－1）个1和（n＋1）个0组成的序列为σ序列（仅仅是一个记号，没有任何特殊的含义），这样的序列共有

在一个非法序列中，存在某个k，使得序列前k个项中1的个数少于0的个数。即存在k使得前k项中1的个数比0的个数刚好少1个，取其中最小的k。那么这个序列的后（2n－k）项中1的个数刚好会比0的个数多1个。将后2n－k项中的0换为1，1换为0，于是得到一个新的序列：由（n－1）个1和（n＋1）个0组成的序列，那么这是一个σ序列。这样我们就已经成功地将一个非法序列对应到唯一一个σ序列。所以，非法序列和σ序列一一对应。

同理，σ序列也可一映射到一个非法序列。对任意一个σ序列，存在某个k，使得序列的前k项中1的个数少于0的个数（因为只有n－1个1，而有n＋1个0）。进一步地，存在某个k，使得序列前k项中1的个数比0的个数刚好少一个，取其中最小的k。那么这个序列的后（2n－k）项中1的个数刚好会比0的个数少1个。将后（2n－k）项的0换成1，1换成0，于是得到一个新的序列：由n个1和n个0组成。而这个序列正是一个非法序列（因为前k项中1的个数比0的个数少）。我们又成功地将一个σ序列对应到唯一一个非法序列。

1 盛 骤，谢式千，潘承毅.概率论与数理统计［M］.高等教育出版社，2006.

2 吴 翊，吴孟达，成礼智.数学建模的理论与实践［M］.国防科技大学出版社，2002.

3 张珠宝.数学建模与数学实验［M］.高等教育出版社，2005.