异常工况下双进双排气门-导管许用间隙值研究

许春霞，董 兵，胡 瑞，刘佐民

(1.武汉理工大学机电工程学院，湖北 武汉 430070;2.济南沃德汽车零部件有限公司技术部，山东 济南 250022)

现代车用柴油机除了必须具备良好的燃油经济性和动力性外，还需在较大转速及负荷变化范围内满足日益严格的排放法规的要求，4气门技术是实现这一目标最有效的方法之一。与传统的柴油机相比，4气门柴油机可以增大气门面积，减少高速时的泵吸功，降低换气损失，提高充气效率[1]。目前，世界各大汽车公司新开发的轿车大多采用4气门结构。但国内4气门的使用还不广泛，且对气门-导管间隙方面的研究大都是在正常工况下，而异常工况下气门-导管间隙对气门应力特性的影响较大，特别是对气门第二热点应力的分布[2-6]。虽然在不同的初始条件下分析得出的具体数据可能不一样，但其应力的变化趋势是相同的。基于此，笔者以气门偏摆落座理论模型为基础，以柴油机双进双排气门为研究对象，分析异常工况(气门偏摆落座)下气门-导管间隙ΔD、锥面角β对双进双排气门应力特性的影响。由于笔者主要讨论由ΔD和β变化而引起的第二热点应力及表面最大应力的分布特性，因此，其变化规律还能反映许用间隙ΔD的变化范围。

1 双进双排气门的数值分析

双进双排气门结构中两气门杆端固定在气门桥中，因此，其工作时两气门间的偏摆角受限于气门-导管间隙ΔD。在正常工况下，气门的偏摆落座取决于气门-导管的安装间隙ΔD，其值很小，因此其偏摆角也很小，可忽略不计;但当气门杆或导管产生磨损后，ΔD增大，此时气门落座的偏摆角将增大。图1为双进双排气门偏摆落座示意图。

设图1中的偏摆角为α，则:

由式(1)可知，当导管长度L为定值，则ΔD越大，气门偏角越大，而由于气门桥的限制，气门的偏摆主要发生在盘部，即气门盘与气门座锥面发生偏斜，在此情况下，气门-气门座偏斜角将增大气缸内热气流对气门杆第二热点的冲击，从而导致热点处气门杆材料屈服强度的下降和热应力的增大，直接影响气门的寿命，甚至气门杆断裂。

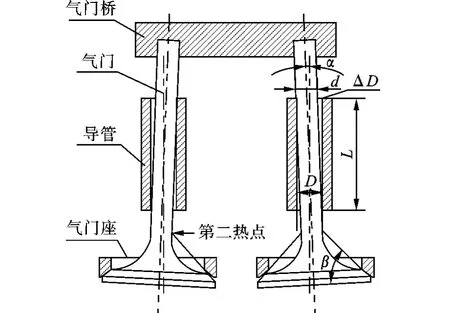
图1 双进双排气门偏摆落座模型

为此，笔者采用有限元法分析ΔD、β及其耦合作用对该热点应力的影响，并探讨ΔD的许用值范围。

1.1 模型建立

为便于分析，笔者选用气门常用材料21-4 N[7]，其密度为 7 900 kg/m3，泊松比为 0.3，弹性模量为210 GPa，切变模量为81 GPa，热膨胀系数为1.3×10-6，热传导系数为25.96;气门导管材料为HT250，弹性模量为140 GPa，泊松比为0.25;气门座圈和气门桥材料为42CrMo，弹性模量为206 GPa，泊松比为 0.3。

利用Pro/E软件对气门、气门座、气门导管，以及气门桥进行参数化三维实体建模，参数化模型建立后可以直接调用该零件或设置参数变量值来获取所需的零件，从而提高建模效率。然后再对所建立的各个零件进行装配，最后将气门装配体导入Ansys-workbench进行分析，由于Pro/E与Ansys-workbench之间的无缝连接使得模型的数据不会丢失，较好地保证了分析的准确性。

1.2 网格划分

计算精度取决于网格划分的精度，网格划分越细密计算精度越高，但同时会增加求解计算的时间和存储空间，理想的网格密度是计算结果不随网格的加密而改变的密度。网格划分时，实体一般采用10节点的4面体单元和20节点的6面体单元进行划分。为提高分析的准确性，气门选择6面体优先，单元尺寸为2 mm，其他均采用默认设置进行网格划分。

1.3 边界条件分析

气门边界条件取决于发动机型号，其变量涉及气门落座力、气门结构尺寸、气门弹簧预紧力、气缸内燃气对气门盘部的背压力，以及气缸热气流温度等。图2为由偏摆落座而引起气门应力分布特性的分析流程图。

为便于进行有限元分析，气门座和气门导管设为固定约束，气门桥与气门之间的接触设为不分离。为提高分析的准确性，考虑到施加在气门桥中间的力会对气门产生力矩，因此在分析中将该力设置为远程力，它将在气门桥中间的作用点处产生一个等效的力和由于偏置所引起的力矩[8-9]。图3和图4分别为双进双排气门结构及约束模型和在异常工况下，ΔD和β对其应力特性影响的云图。

图2 建模及分析流程示意图

图3 双进双排气门结构及约束模型

图4 气门应力云图

2 结果分析与讨论

2.1 ΔD对气门应力的影响

图5为气门-导管间隙ΔD对气门应力特性的影响，由图5可以看出:偏摆落座时，气门第二热点应力及最大表面应力随ΔD的变化而改变，当ΔD≤0.22 mm时，其随ΔD增大略微呈减小趋势，且变化比较平稳;而当ΔD＞0.22 mm时，随着ΔD的增加，第二热点应力呈急剧增大趋势，最大表面应力先急剧增大后略呈减小趋势，但此时间隙值ΔD已较大，较大的ΔD将使气门偏摆程度增加，甚至使润滑油流失，使气门的工作条件更加恶劣从而更易失效。另外，ΔD也不能太小，由于气门在工作过程中受到气缸内部高温燃气的作用，工作温度较高，热膨胀量较大，ΔD太小易使气门在导管中运动时发生卡死现象，特别是在异常工况下。因此，ΔD不能过大也不能过小，其最佳取值为0.22 mm。

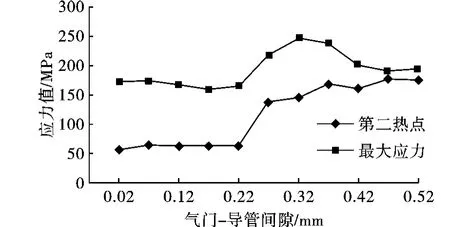
图5 ΔD对气门应力的影响

2.2 ΔD与β耦合对气门应力的影响

锥面角β是气门的一个主要结构参数，β较小，气门盘部相对较薄，在承受热载荷和力载荷时就容易变形，变形过大就会产生失效;β较大时，气门盘部变厚，会增加气门的质量，从而增加双进双排气门机构的整体质量。在影响气门落座力的因素中，气门机构的整体质量对气门落座力的影响最大[10]，而落座力是分析气门应力特性的边界条件之一。因此，需探讨β的合理取值。

图6 分析了 β =30°、β =45°及 β =60°时，ΔD 对气门第二热点应力的影响，由图6可以看出，ΔD≤0.22 mm 时，β =30°、β =45°及 β =60°的气门第二热点应力都随ΔD增大而减小;而ΔD＞0.22 mm时，β=30°、β=45°的气门第二热点应力随ΔD增加而增大，特别是β=45°时的气门第二热点应力值随ΔD增加而急剧增大，但β=60°时的气门第二热点应力随ΔD增大呈先减小后缓慢增大的趋势。

图6 ΔD与β耦合对气门第二热点应力的影响

图7为ΔD与β耦合对气门表面最大应力的影响，由图7可以看出:当ΔD≤0.22 mm时，气门表面最大应力随ΔD的增加而减小，ΔD=0.22 mm时，气门表面最大应力达到最小;而 ΔD＞0.22 mm时，其呈现先增大后减小趋势。由上面的讨论可知，气门-导管间隙值ΔD不宜过大，综合考虑，其最佳值为0.22 mm。下面将研究ΔD=0.22 mm时，β对气门应力的影响规律。

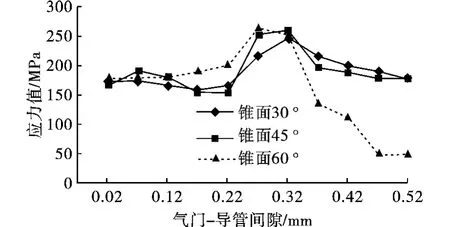
图7 ΔD与β耦合对气门表面最大应力的影响

图8为间隙ΔD=0.22 mm时，锥面角β对气门应力的影响曲线。由图8可知，ΔD=0.22 mm时，第二热点的应力随β的增加而呈先减小后增大的趋势，其中β为45°时第二热点的应力最小，这也与图5的分析相吻合;而气门表面最大应力随β增加而呈线性增大趋势，其中β＞45°时，其增大的趋势更明显。在气门的设计中，β过大会增加气门的质量，进而增大气门与气门座接触时的落座力，而β过小易使气门盘部变形，综合考虑，β的合理值为45°。

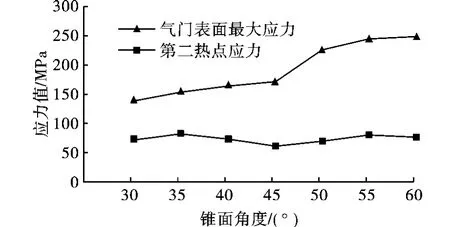
图8 锥面角β对气门应力的影响

3 结论

(1)研究表明，气门-导管间隙对双进双排气门偏摆落座影响较大，其主要特征反映在气门第二热点应力及表面应力状态上。一般地，气门第二热点应力及表面最大应力随ΔD增大而增大，但存在临界值，因此，为了控制气门使用寿命，气门-导管间隙应控制在合理范围内。

(2)气门偏摆落座时，ΔD对气门第二热点应力及气门表面最大应力影响较大。在ΔD≤0.22 mm时，第二热点应力呈减小趋势且变化较稳定，而在ΔD＞0.22 mm时，第二热点的应力随间隙值增大急剧增大;气门最大表面应力也在ΔD=0.22 mm时达到最小。

(3)气门-导管间隙ΔD和气门锥面角β对气门应力的影响存在互耦性，当ΔD增加时，气门第二热点应力及表面最大应力都随之增加，而ΔD=0.22 mm时，第二热点应力随β增加而呈先减小后增大的趋势;气门最大表面应力随β增加而增大，特别是β＞45°时。综合考虑得出，合理的ΔD和β分别为:ΔD=0.22 mm和β=45°。

[1] 倪计民，高征.车用柴油机四气门结构设计研究[J].内燃机学报，2005，23(4):357-362.

[2] 谢勇.发动机四气门配气机构系统分析研究[D].上海:上海交通大学图书馆，2009.

[3] 倪洪义.车用气门主要工作部位失效模式分析[J].发动机制造，2010，21(4):74-76.

[4] 黄华，刘佐民.基于导管间隙的气门偏摆落座特性的仿真系统研究[D].武汉:武汉理工大学图书馆，2010.

[5] 李厚佳，刘佐民.基于ANSYS的气门盘部设计参数对应力分布影响的研究[J].机械，2008，35(4):31-34.

[6] 陆际清，沈祖京，孔宪清，等.汽车发动机设计[M].北京:清华大学出版社，1993:277-336.

[7] 陈凯俊，刘佐民.气门偏心对其应力分布的影响[J].机械设计与制造，2007，33(9):40-42.

[8] 李兵，何正嘉，陈雪峰.ANSYS Workbench设计仿真与优化[M].北京:清华大学出版社，2008:12-46.

[9] 张朝晖.ANSYS11.0结构分析工程应用实例解析[M].北京:机械工业出版社，2008:100-168.

[10] 卢平，汪伟，刘佐民.基于Simulink的发动机落座力仿真分析[J].武汉理工大学学报，2003，25(11):73-76.