基于删扩的速率兼容LDPC码的性能研究
徐 晋,赵德周,李成军
(武汉理工大学信息工程学院,湖北 武汉 430070)
低密度奇偶校验(low-density parity-check,LDPC)码是由GALLAGER所提出的一种具有稀疏校验矩阵的线性分组码[1],经过几十年的沉寂,1999年,MACKAY重新发现LDPC码是一种性能十分接近香农限的好码[2]。LDPC码的构造可归为两类,一类是基于随机或伪随机构造,另一类是基于代数法构造。在构造LDPC码校验矩阵时,随机构造方法不利于硬件实现,于是人们想到利用代数几何的方法来构造LDPC码的校验矩阵,于是产生了准循环LDPC码,即QC-LDPC码(quasi-cyclic LDPC codes)。基于准循环扩展QCE(quasi-cyclic extension)技术设计的非规则RA(irregular repeat-accumulate,IRA)码,由于设计简单,编码快速等优势已被列入IEEE802.16e标准[3]。
为了适应不同的传输环境,满足不同的服务质量要求,通信系统需要前向纠错编码的码率甚至帧长自适应地根据信道环境做出相应调整,即自适应信道变化的编码器。DVB-S2中采用的LDPC码就设置了两种编码长度以及21种码率,极大地改善了系统性能[4]。码率及帧长的自适应变化虽然可以由多个编码器和译码器实现,但此举必然会导致编译码器的复杂度过高,故如何设计复杂度较低的速率兼容码(变码率变帧长)显得更加重要,且已成为当前编码领域的研究热点。
所谓的速率兼容码(rate-compatible codes),即较高码率的码字的校验比特是嵌套在较低码率的码字的校验比特中的。目前常用的速率兼容码有BCH码、卷积码(rate-compatible punctured convolutional code,RCPC)和 Turbo码(rate-compatible punctured turbo code,RCPT)。发送端将母码经过不同的删除或扩展得到不同的码率,只需要一个编码器。接收端已知被删除比特或增加比特的位置即删除矩阵或扩展矩阵,因此可以按照母码进行译码,也只需要一个译码器。也就是说,整个系统中使用一对编译码器便可以完成速率兼容码的编码和译码。
1 准循环LDPC码(QC-LDPC Codes)
QC-LDPC码是LDPC码的一个非常重要的子集,属于构造码。LDPC码由其奇偶校验矩阵H确定。QC-LDPC码的奇偶校验矩阵H由一系列相同大小的稀疏循环矩阵给出,也就是说它的奇偶校验矩阵是准循环形式的。例如,IEEE802.16e标准中QC-LDPC码由m×n的矩阵H定义,其中m为校验位的位数,n为码长的位数。其校验矩阵H是由基础矩阵(Hb)mb×nb膨胀得到的,其中Hb如式(1)所示,膨胀因子z=n/24,m=mb× z,n=nb× z。
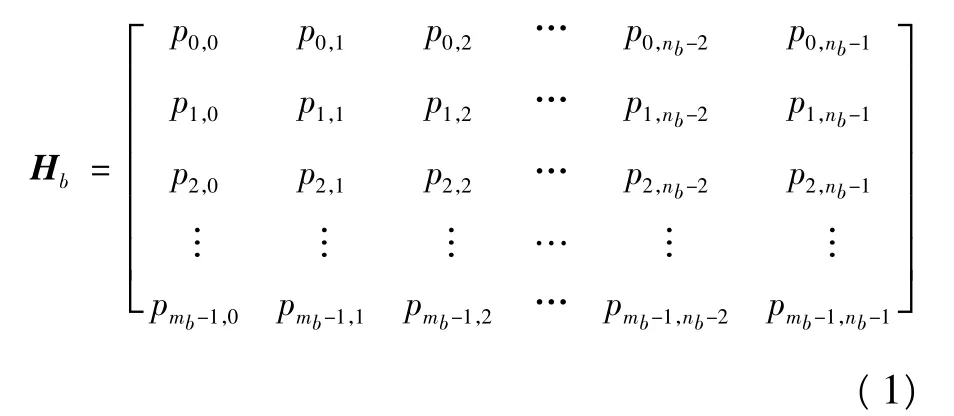
用 pi,j=-1 表示 z× z的全 0 矩阵,pi,j≥0 表示z×z的单位矩阵按列循环移位pi,j后的矩阵。由全0矩阵替换Hb中的-1,由循环移位的单位阵替换Hb中的非负元素,就可以由Hb扩展成H矩阵。若将校验矩阵 Hb分成两部分 Hb=[(Hb1)mb×kb|(Hb2)mb×mb],Hb1称为信息子集,Hb2称为冗余子集,Hb1对应信息比特,Hb2对应校验比特。Hb2被进一步分成两部分,如式(2)所示。hb是非负的元素为奇数个的列向量,对应H中奇数个单位方阵循环右移,H'b2为双对角线结构矩阵,对应H的双对角线结构。这种结构的码又称为重复累积码(RA码),具有类下三角形式,该下三角矩阵具有双对角线形式。
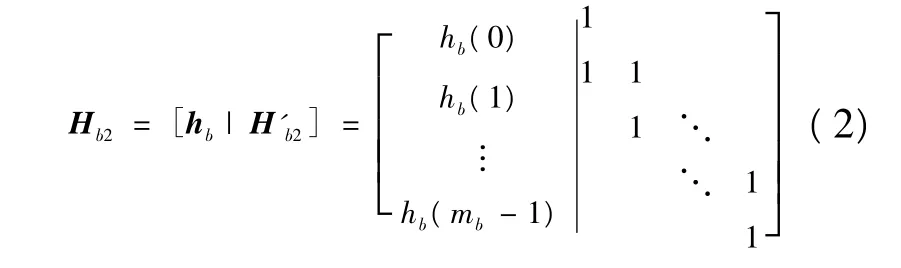

这种基于单次扩展的重复累积码由于其校验矩阵也是稀疏的,因此是LDPC码的一种,又由于其准循环结构,它又属于QC-LDPC码。该码固然有良好的性能,但是在构造速率兼容码时,为了使较高码率的校验比特能够嵌入到较低码率的码字中,要求扩展的校验阵的右上部分为全0阵。这就要求母码拥有完全下三角形式。
2 速率兼容QC-LDPC码的构造方案
目前,速率兼容LDPC码主要是凿孔和扩展构成的多码率LDPC码,该类多码率LDPC码的所有码率的编码矩阵和校验矩阵都相同,通过对信息位的凿孔实现码率的调整,是一种变码长的多码率的实现。
显然IEEE802.16e中的QC-LDPC码的结构使得在构造速率兼容码时,无法对其进行扩展。然而,可以在其基础上进行改进,得到如下具有完全下三角矩阵的校验阵,作为速率兼容码的母码校验矩阵。
为了构造速率兼容的LDPC码,笔者使用顺序删除和扩展检验矩阵的方法[5]。以上述mb=12,nb=24的矩阵为母码的校验矩阵,母码的速率R=1/2。膨胀因子 z=96,故为(2304,1152)码。通过对母码校验矩阵的扩展来构造较低码率的码字,相对的,通过对母码校验矩阵的顺序删除来得到较高码率的码字。无论是对校验矩阵进行删除还是扩展,都保持校验矩阵信息子集不变,都为kb=nb-mb=12。通过对校验矩阵进行顺序扩展来得到较低码率的码字,如图1所示;将校验矩阵沿对角线方向进行扩展,扩展矩阵B1,B2是具有完全下三角形式的r×r的方阵,如图2所示。扩展后的校验矩阵右上方是全零元素,左下方C1和C2是稀疏矩阵。C1和C2可采用PEG方法构造,且避免使校验矩阵出现围长为4的短环。PEG算法[6]的基本思想就是通过展开Tanner图,找到距离变量节点最远的校验节点,然后在它们之间添加所需要的边,这样新添加的边对Tanner图影响最小,得到的Tanner图具有最大的围长。可见,经扩展后的码率为Rn=(nb-mb)/(nb+r),当 r=2 时,Rn=0.46。
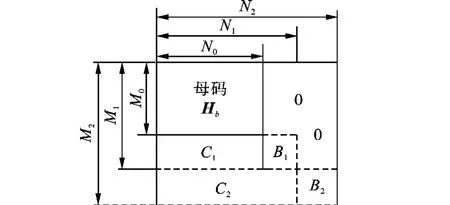
图1 顺序扩展方案
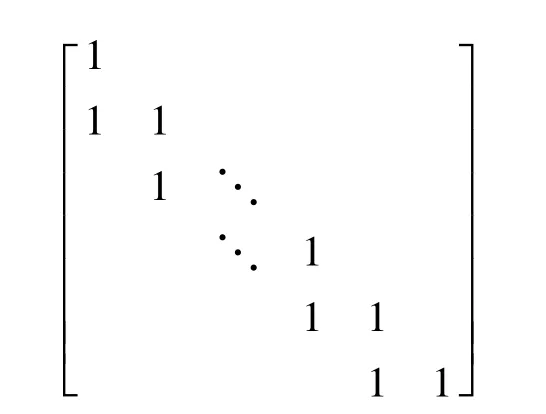
图2 B1、B2具有完全下三角的扩展矩阵
顺序删除校验矩阵的最下面r行和最右边r列,这样既能得到较高码率的码字又能保证高码率的码字包含在低码率的码字之中,所得到的新码字的码率为R'=(nb-mb)/(nb-r)。可见,当r=2时,码率R'=0.55;当r=4时,码率R'=0.6。
3 LDPC码的线性时间编码
RU分解算法给出了线性编码的方法,首先将校验矩阵进行分块[7]:
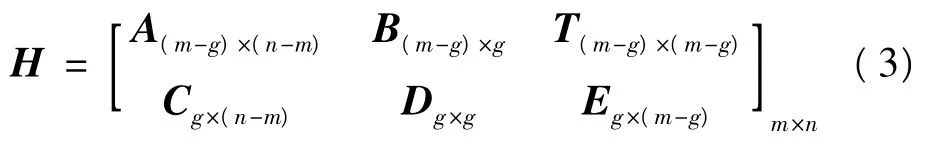
其中,T为下三角矩阵,则H可转化为如图3所示的近似下三角校验矩阵。
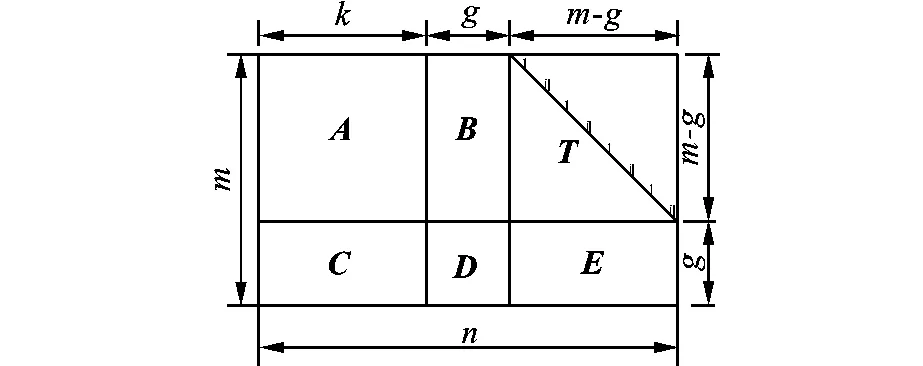
图3 近似下三角校验矩阵
对于所使用的RC-QC-LDPC码来说,B=C=D=E=φ,因此,分块矩阵可以进一步简化成如图4所示的完全下三角校验矩阵。在图4中,A为m×k阶的矩阵,T为m×m阶的具有完全下三角形式的矩阵。将输入编码器的信息比特以z比特为一组,即 vi=[vi1,vi2,…,viz],则输入的信息比特可表示为 V=[v1,v2,…,vk]T,同样将校验比特以 z比特为一组,即 pi=[pi1,pi2,…,piz],则编码器得到的校验比特可表示成P=[p1,p2,…,pm]T。由线性分组码的编码可知:
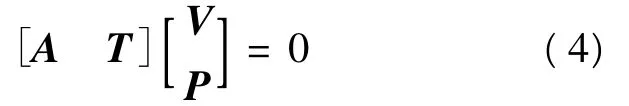
即A·V+T·P=0,式中所有的求和均为模
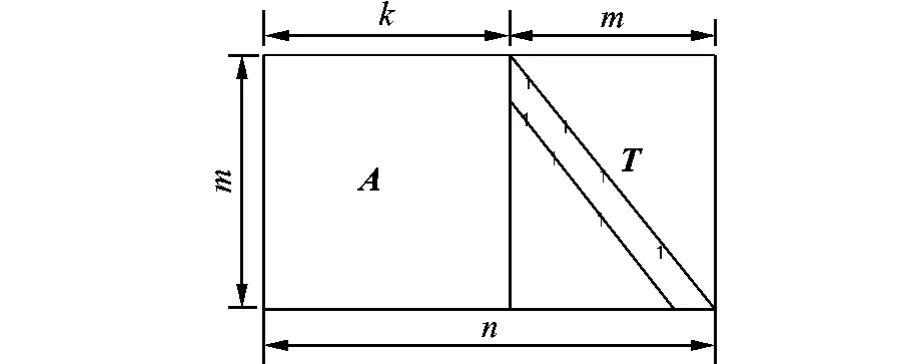
图4 完全下三角的校验矩阵
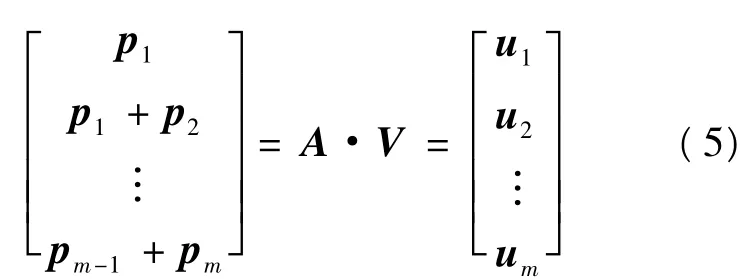
得到 p1=u1,p2=u1+u2,p3=u1+u2+u3,
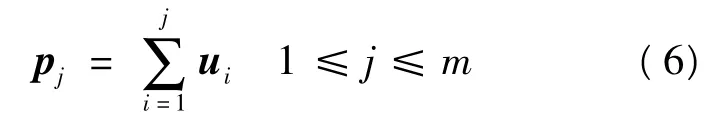
因此关键的计算量在于求解矩阵A·V,由于A的元素是由单位矩阵循环移位置换而得到的,故A·V可以在线性时间内编码,从而实现QC-LDPC码的线性时间编码,编码的复杂度为O(n)。矩阵A·V可以通过移位寄存器电路和模二和电路来实现,硬件电路简单。
4 LDPC码的解码
LDPC码译码算法中,普遍采用置信传播BP算法和对数似然比置信传播LLR-BP算法[8-10]。它们是基于LDPC码的图论模型,在比特节点与校验节点之间所传递的是信息位和校验方程的可靠性信息。迭代译码方法可以采用并行结构实现。由于BP算法的实现复杂度较高,实时性不好,人们提出改进的算法,典型的就是最小和MS算法及其改进算法。最小和算法是在LLR-BP算法的基础上进行简化得到的,即利用gallager函数φ(x)的单调递减性及φ-1(x)=φ(x)。
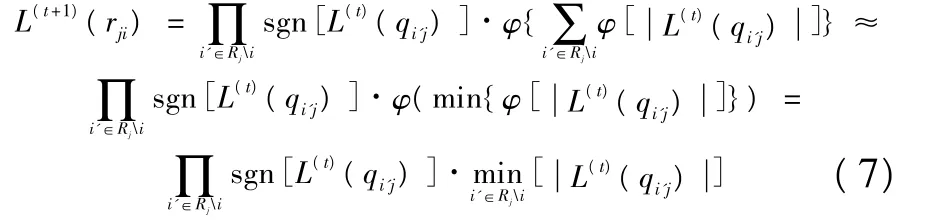
实现最小和算法的步骤为:
(1)初始化 L(0)(qij)=L(pi)=2yi/σ2。
(5)做判决,若 L(qi)>0则判 ci=0,否则ci=1。
如果c·H'=0或到达最大迭代次数,则译码结束,否则令t=t+1跳回步骤(2)继续迭代。
5 仿真结果及性能分析
在加性高斯白噪声信道下,信号采用BPSK调制,采用最小和积算法,最大迭代次数30次,对构造出的速率兼容码进行仿真。对于以下的码字(2304,1152),(2112,1152),(1920,1152),(2496,1152)仿真结果如图5所示。
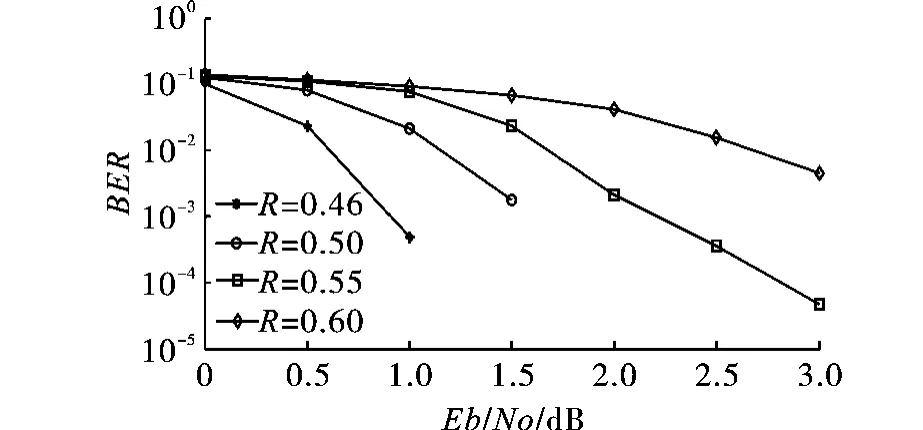
图5 速率兼容码的误码率性能
从图5可以看出,对母码矩阵(码率1/2)进行扩展后得到码率为0.46的码字,误码性能明显变好,当误码率为10-3时,约有0.5 dB的信噪比增益。添加检验比特可以提高误码性能,对母码进行删除之后得到码率为0.55和0.60的码字,误码性能变差,当误码率为10-3时,分别约有0.5 dB和1.0 dB的信噪比损失,打孔会造成性能变差。
6 结论
笔者通过仿真验证了实现线性时间解码和复杂度较低的解码,以及通过顺序删除和顺序扩展构造速率兼容的QC-LDPC码的可行性,同时证实了该方法具有一定的广泛性,并为LDPC码在自适应编码中的应用提供了参考依据。
[1] GALLAGER R G.Low density parity check codes[J].IRE Transactions on Information Theory,1962,8(1):21-28.
[2] MACKAY D J C.Good error correcting codes based on very sparse matrices[J].IEEE Transactions on Information Theory ,1999,45(2):399-431.
[3] IEEE802.16e:part 16.Air interference for fixed and mobile broadband access system[S].
[4] ALBERTO M,VITTORIA M.DVB-S2:the second generation standard for satellite broad-band services[J].Proceedings of the IEEE,2006 ,94(1):210-216.
[5] JOEHONG K.The design of efficently-encodable rate-compatible LDPC codes [J].IEEE Transaction on Communications,2009,57(2):365-375.
[6] HU X Y,ELEFTHERIOU E.Regular and irregular progressive edge-growth tanner graphs[J].IEEE Transactions on Information Theory,2005,51(1):386-398.
[7] RICHARDSON T,URBANKE R.Efficient encoding of low-density parity-check codes[J].IEEE Transactions on Information Theory,2001,47(2):638-656.
[8] CHEN J H,FOSSORIER M.Near optimum university belief propagation based decoding of low density parity check codes[J].IEEE Transactions on Communications,2002,50(3):406-414.
[9] 吴湛击,王文博.现代信道编码与调制:理论与应用[M].北京:人民邮电出版社,2008:232-236.
[10] 文红,符初生.LDPC码原理与应用[M].成都:电子科技大学出版社,2006:55-63.

