民航行李X光安检图像自适应小波去噪算法
夏 冬 ,韩 萍
(1.中国民航大学智能信号与图像处理天津市重点实验室,天津 300300;2.中国民航大学电子信息工程学院,天津 300300)
爆炸物是威胁公共安全的重要因素,尤其是在机场行李中夹带爆炸物品,将严重的威胁旅客的安全,对其进行检测已成为机场安检领域的重要检测项目之一。利用X光透射式成像原理对行李内物品进行成像探测,由于其具有不必开箱且对受管制的金属器具及爆炸物等有较好的成像探测效果的优点,因此成为机场、港口、车站等重要场所普遍采用的安检装置。安检系统成像过程中,由于受辐射源、探测器、采集电路等因素影响,所采集的图像不可避免的会含有随机噪声,而成像过程中传送带运行不稳定、电源不稳定、传输网络不稳定、移动电话等因素的影响,又会使得所采集的图像含有脉冲噪声,因此有必要对X光安检图像进行去噪处理,以达到处理后用肉眼观察就能对图像进行自动辨别的要求。
小波变换去噪由于具有良好的时频特性而得到迅速发展。小波变换采用了多分辨率的方法,具有低熵性、去相关性和选基的灵活性,在图像去噪领域得到了越来越广泛的应用。1994年,Donoho首次提出了小波阈值这个方法[1-3],由于此方法在Besov空间上可以得到最佳的估计值,而其他的线性估计都达不到与此相同的结果,因此国内外学者以此为基础发展了多种不同算法[4-6]。本文着重讨论小波去噪中的阈值去噪方法。针对软硬阈值去噪方法的缺陷[7,8],提出折中阈值处理算法,并在此基础上对大于和小于阈值的两部分高频小波系数进行自适应处理,取得了较好的效果。
1 基于小波的去噪方法
1.1 小波去噪流程
小波的标准去噪方法由小波变换、阈值处理、小波反变换三步组成[9-11]:
1)在小波变换部分有两个问题需要研究:一是根据小波性质选择适合的小波函数进行分解;二是分解层数的确定,分析合理的分解层数以达到最佳的去噪效果;
2)在阈值处理部分主要是改变得到的小波系数,在这一步中也有两个重要问题需要解决:一是阈值T的选择;二是去噪估计函数的选择及改进;
3)最后通过小波反变换,得到无噪的图像。
1.2 小波函数的选择
基函数的正交性使相应的表示系数能容易地用内积计算,然而,这些变换一般所揭示的是信号的整体性质,难以表征其局部性质。小波变换具有局域处理的优点,其窗宽是可变的,在高频时用窄窗口,在低频时则使用宽窗口[5,12]。
同傅里叶分析不同,小波分析的基(小波核函数)不是唯一存在的(傅里叶分析的核函数是eiθ),所有满足小波条件的函数都可以作为小波函数,那么小波函数的选取就成为了十分重要的问题。实际选取小波的标准主要有以下三种:
自相似原则:对二进小波变换(因为在正交小波变换中,取样的方式就是按小波函数取样的,所以不存在这个问题)如果选择的小波对信号有一定的相似性,也就是在下式的基础上若x2j(t)和f(t)有某种程度的相似,则变换后的能量就比较集中,可以有效减少计算量。
判别函数:针对某类问题,找出一些关键性的技术指标,得到一个判别函数,将各种小波函数代入其中,得到一个最优准则。
支集长度:大部分应用选择支集长度在5~9之间的小波,因为支集太长会产生边界问题,支集太短,消失矩太低,不利于信号能量的集中。
2018年10月16日,全国农民专业合作社质量提升整县推进试点工作现场会在江苏省苏州市召开。农业农村部副部长韩俊出席会议并讲话。
在实际的工程应用中,因为信号的信息量实在太大,难以找到合适的模式,所以只能实际经验中获取,小波函数的主要性质还包括对称性、消失矩阶数和正则性等。
对称性在图像处理中用以避免相移,消失矩阶数大的小波变换使能量更集中,在压缩中用处很大,正则性好的信号重构过程比较光滑。一般来说,支集长度越长,消失矩和正则性越高。
1.3 分解层数的确定
分解层数对去噪结果的影响很大,去噪后信号的信噪比随着分解层数的增加而迅速增加。在超过某个层数之后,去噪后信号的信噪比不但没有提高,反而有较大下滑。所以,确定一个合适的分解层数才能取得较好的去噪效果(分解层数决定着去噪效果),分解层数过少会造成除噪后信噪比提高不多,分解层数过大,虽然增加了运算量,但效果改善不大甚至下滑的情形。可以借鉴传统基于熵的标准来确定小波分解层数n。对于给定灰度图像x(i,j),其信息熵确定义为
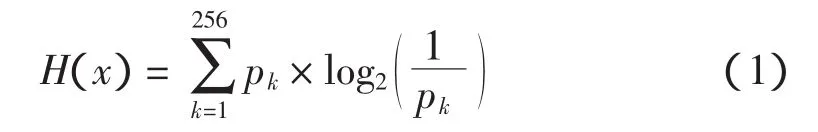
其中pk为图像中灰度级为k的点所占的比例。随着分解层数的增加,第n层的细节信息熵会减小,可认为当第n层的细节信息熵小余原图像信息熵H(x)的0.5%时就没有分解的必要了。
1.4 阈值估计
小波阈值去噪方法的一个关键因素是对阈值的具体估计。如果阈值太小,去噪后的信号仍然有噪声的存在;相反阈值太大,重要图像特征又将被虑掉,从而引起偏差。从直观上讲,对于给定的小波系数,噪声越大,阈值就越大[1,13]。
由于在实际应用中噪声的方差很难事先知道,通常采用的是绝对中值估计法(MAD)

其中:Wi(m,n)为第i层的高频小波系数;0.674 5为估计系数;MAD(x)为求中值的函数,则阈值T为

其中:N为信号长度。
硬阈值法认为:小于阈值的小波系数是噪声分量,予以全部去除;大于阈值的小波系数是信号分量,予以全部保留。
软阈值法认为:小于阈值的小波系数是噪声分量,予以全部去除;大于阈值的小波系数,其主要成分是信号分量,予以收缩后保留。
其软硬阈值函数表达式如下式表示,其波形如图1所示。
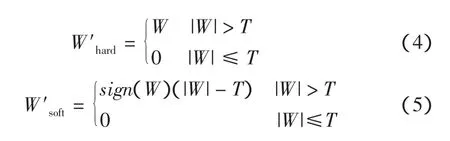
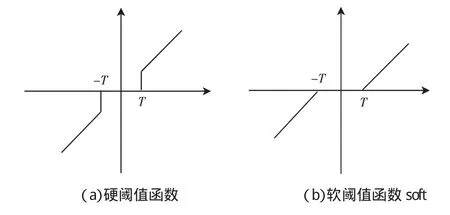
图1 软硬阈值函数图Fig.1 Hard and soft threshold function
2 民航行李X光安检图像去噪方法
软硬阈值处理方法虽然在实际中得到广泛的应用,也取得了较好的效果,但该方法也有一些潜在的缺点。如硬阈值方法中,W′hard在T处是不连续的,利用W′hard重构所得的信号可能会产生一些振荡;由软阈值方法估计出的W′soft虽然整体连续性好,但是当时,W′soft与W总存在恒定的偏差,直接影响着重构信号的逼近程度。鉴于此,可对软硬阈值法进行折中,折中后的处理函数如下式表示,其波形如图2所示。
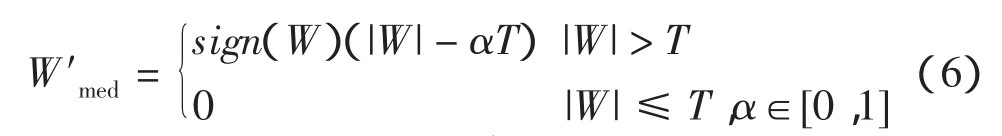
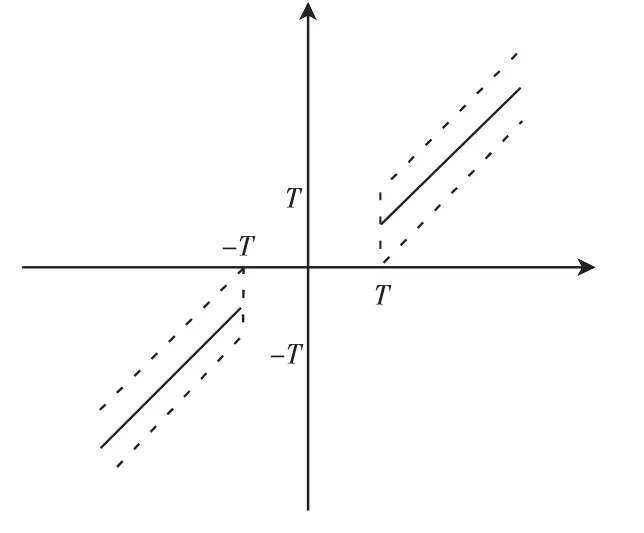
图2 折中阈值函数图Fig.2 Median threshold function
不难发现,当α=0时等同于硬阈值方法,当α=1时等同于软阈值方法。
在进行软硬阈值及折中算法中存在两个问题:一是在阈值处理时直接将第一类小波系数置为0,这在很大程度上影响了重构信号使其局部分辨率下降;二是忽略了边缘的检测,这导致重构信号丢失了部分边缘信息。针对这两点,分别对大于和小于阈值的两部分进行自适应处理,处理过程如下:
将原信号经小波变换后的细节信号W细分为信号部分和噪声部分:若|W|≥T,则归为信号部分,记为 WS;若|W|< T,归为噪声部分,记为 Wn,将 Wn进行修正(λ 为修正系数,0.37≤λ≤0.45)

然后以WS每一元素为中心置长度为3的窗口,设窗口内WS元素数为k,若k≥2说明这几个WS元素可能代表一定的边缘信息,这样中心元素按照折中阈值处理(折中系数取0.4,也即α=0.4)中有效信号情况处理;否则说明这个元素可能由噪声造成,中心元素乘以修正系数λ以减少它的小波分解系数值
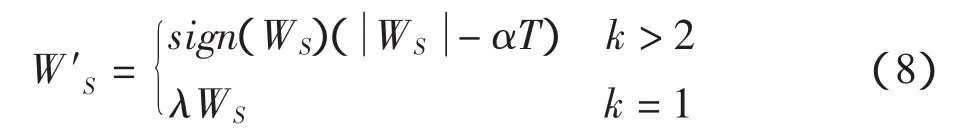
同理,对于Wn每一元素为中心置一长度为3的窗口,设窗口内Wn元素数为k,若k≥2说明这几个WS元素可能代表噪声部分,这样中心元素用0代替,否则保持不变
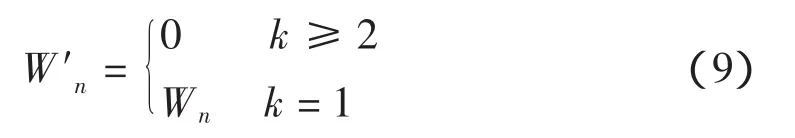
最后利用W′s和W′n进行小波重构,得到去噪后的图像。
3 实验结果与分析
为了检验算法的可实行性和最终处理的效果,实验数据使用Tennessee大学提供的实际采集的X光安检图像,在570×557像素的图像上加入方差为0.02的高斯白噪声。在小波基的选择上,选择sym4小波来做小波分析处理,因为sym小波具有更好的对称性,更适合于图像处理,减少重构时的相移。在分解层数的选择上,用信息熵方法来确定对含噪图像的最佳分解层数,仿真实验证明分解到第4层后信噪比会迅速下降,因此,分解层数为3层时效果最好。最后,对含有高斯随机噪声的X光安检图像分别用硬软阈值和本文提出的自适应阈值方法进行去噪实验。
图3(a)为含噪图像。图3(b)为硬阈值法去噪结果图,图像较模糊。图3(c)为采用软阈值法去噪结果图,与图3(b)相比,图像质量有提高,噪声得到了抑制,但图像仍有些模糊,边缘不明显。图3(d)是本文所提出的自适应阈值法,去噪后的视觉效果比图3(b)、图3(c)好,在去噪的同时,较好地保留了图像边缘特征。

采用峰值信噪比和均方误差对去噪图像进行了定量分析比较。均方误差MSE及峰值信噪比PSNR公式定义如下
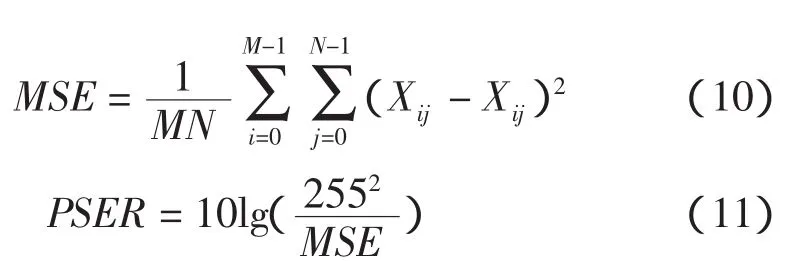
其中:Xij为原X光安检图像像素灰度值;X′ij为去噪图像像素灰度值。
可见本文提出的方法,从信噪比SNR、峰值信噪比PSNR和均方误差MSE指标衡量降噪后的图像在这些个指标上都有所改进,如表1所示。
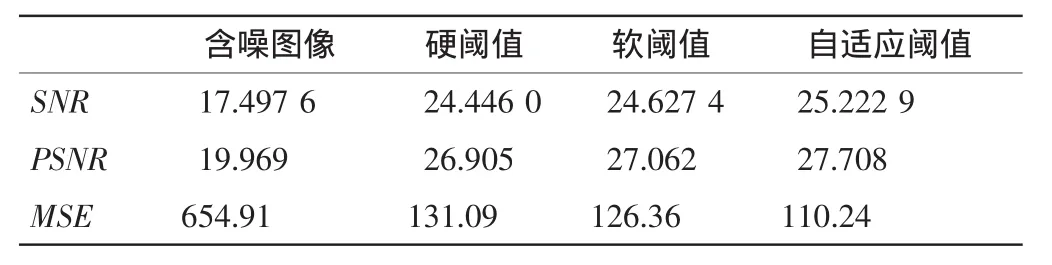
表1 图像去噪后的信噪比、峰值信噪比及均方误差Tab.1 Performance comparison of different algorithms
4 结语
本文给出了一种小波自适应阈值方法对X光安检图像进行去噪处理,该方法克服了传统方法在对图像进行降噪处理时导致重构信号局部分辨率下降和部分边缘信息丢失问题。实验结果证实,该方法在视觉效果和去噪性能两方面较前两种方法去噪效果好,进一步提高了峰值信噪比,较好地保留图像的边缘信息;且没有增加处理的复杂度,能用于实时处理。去噪后图像已达到安检要求,可以通过肉眼观察对危险物品图像进行辨别。
[1]DONOHO D L,JOHNSTONE I M.Adapting to unknown smoothness via wavelet shrinkage[J].Jounal of the American Statistical Assoc,1995,90(432):1200-1224.
[2]DONOHO D L,JOHNSTONE I M.Ideal spatial adaptation via wavelet shrinkage[J].Biometrika,1994,8l:425-455.
[3]DONOH0 D L.Denoising by soft-thresholding[J].IEEE Trans on Information Theory,1995,3:613-627.
[4]GRACE CHANG S,BIN YU,VATTERELI M.Adaptive wavelet thresh olding for image denoising and compression[J].IEEE Trrans.Image Processing,2000,9:1532-1546.
[5]ZHANG XIAOPING,DESAI M D.Adaptive denoising based on SURE risk[J].IEEE Signal Processing Letters,1998,5(10):265-267.
[6]GRACE CHANG S,BIN YU,VATTERELI M.Spatially adaptive wavelet thresholding with context modeling for Image denoising[J].IEEE Trans.Image Processing,2000,9:1522-1530.
[7]WEI D,RAJASHEKAR U,BOVIK A C.Wavelt denoising for image enhancement[M].Second Edition.Handbook of Image and Video Processing,2005:157-165.
[8]CHEN G Y,BUI T D,KRZYZAK A.Image denoising with neighbour dependency and customized wavelet and threshold[J].Pattern Recognition,2005,38(1):115-124.
[9]FU JIN,PAUL FIEGUTH,LOWELL WINGER,Image Denoising Using Complex Wavelets and Markov[C]//ICIAR 2005,LNCS 3656,2005:73-80.
[10]IVANA DUSKUNOVIC,ALEKSANDRA PIZURICA,GJENNA STIPPEL,et al.Wavelet Based Denoising Techniques for Ultrasound Images[C]//Proc of the IEEE Engineering in Medicine and Biology Society Conference 2000,4:2662-2665.
[11]RAFAEL C.GONZALEZ,RICHARD E WOODS.数字图像处理[M].北京:电子工业出版社,2005.
[12]WEYRICH N,WARHOLA G T.Wavelet shrinkage and generalized cross validation for image denoising[J].IEEE Trans.On Image Processing,1998,7(1):82-90.
[13]DONOHO D L,STONE J.Wavelet shrinkage aaymptopia[J].Jouranl of Royal Statistical Society,1995,57(2):301-369.

